Раздел 3. Аналитические и численные методы исследований оснований и фундаментов
Рис. 5. Долевое соотношение площадей для |
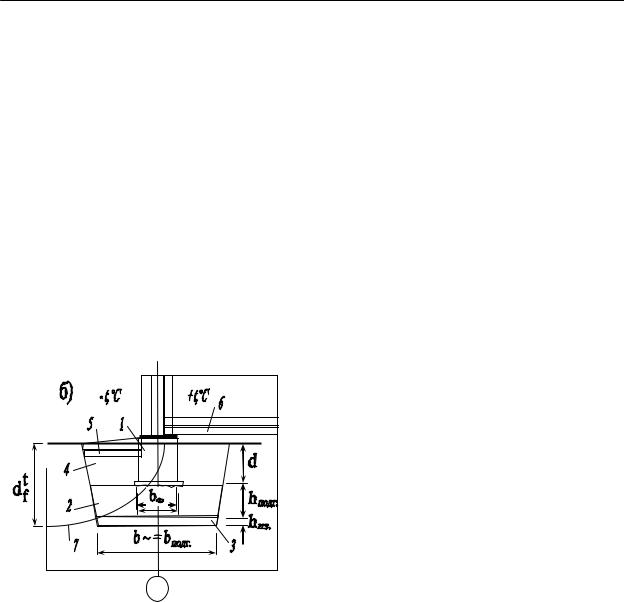
Рис. 6. Расчетная схема |
определения эквивалентной силы. |
|
Литература
1.Бай В.Ф., Еренчинов С.А., Баев М.А. «Исследование работы фундамента в виде клиновидных свайных рам», Сборник материалов IV конференции ТюмГАСУ, Тюмень
2004 г.
2.Бай В.Ф., Еренчинов С.А., Баев М.А. «Определение оптимальных геометрических параметров рамно-козловых свайных фундаментов», Сборник материалов V конференции ТюмГАСУ, Тюмень 2005 г.
3.Бай В.Ф., Еренчинов С.А., Баев М.А. «Экспериментальные исследования рам- но-козловых свай», Сборник материалов VI конференции ТюмГАСУ, Тюмень 2006 г.
4.С.П. Тимошенко, Дж. Гудьер Теория упругости. Москва 1975 г.
5.Галагер Р. Метод конечных элементов. Основы Пер. с англ. – М.: Мир, 1984. –
428с., ил.
УДК 624.131
П.Н. Костюкович (БНТУ, Минск)
ЗАКОНЫ НЕЛИНЕЙНОЙ ДЕФОРМАЦИИ ПРИ КОМПРЕССИОННЫХ И ШТАМПОВЫХ ИСПЫТАНИЯХ ГРУНТОВ БЕЛАРУСИ
На примере компрессионных и штамповых испытаний грунтов приводится обоснование необходимости соблюдения принципа единства прямых (геотехнические прогнозы) и обратных (определение модуля деформации) задач геомеханики, в соответствии с которым решение этих задач должно исходить из одного уравнения — опытного закона деформации. Установлен аналитический вид нелинейных закономерностей, которым подчиняются компрессионное сжатие грунтов ε(σ) и осадка штампов S(σ). Доказывается, что в условиях существования этих закономерностей, имеющих широкое распространение (до 40-90%) в компрессионных и всегда при штамповых испытаниях, в одном и том же грунте
Современные геотехнологии в строительстве и их научно-техническое сопровождение
гуковские модули деформации закономерно изменяются с ростом σ: компрессионные Ek=β0(σ/ε) возрастают, а штамповые ES=f(K,D)(σ/S) падают. Отсюда сделан вывод об относительности законов деформации: законы деформации одного и того же грунта могут быть самыми различными – как линейными, так и нелинейными – в зависимости от граничных условий области деформации.
В инженерной геологии и механике грунтов рассматриваются в основном установившиеся или предельные деформации, когда в любой точке эпюры избыточных давлений σ, создаваемых фундаментом, деформация геооснования достигает предела и не изменяется во времени. Законы предельных деформаций подразделяют на линейные и нелинейные. Среди линейных выделяют два типа законов, принципиально отличающихся друг от друга [2 ,3, 9]:
прямо пропорциональные или однопараметрические, подчиняющиеся перво-
му закону Гука h1 (рис. 1 ):
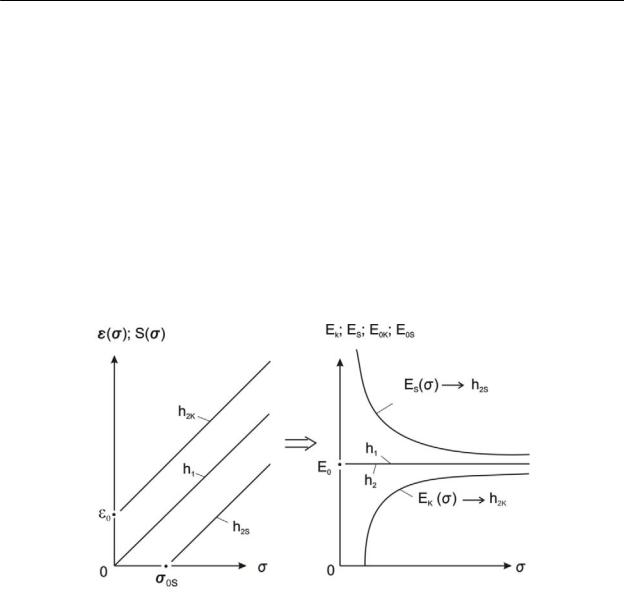
Рис. 1: а вторые (обобщенные) законы Гука h2К иh2S, к которым сводятся "гостовские" методы определения модулей деформации соответственно при компрессионных и штамповых испытаниях грунтов [1]; h1 – первый (прямо пропорциональный) закон Гука – прогнозная прямолинейно-деформируемая модель осадки геооснования с одинаковыми ком-
прессионными и штамповыми модулями деформации E0 E0K E0S ; b функции неус-
тойчивости гуковских модулей деформации при компрессионных EK( ) и штамповых ES( ) испытаниях грунтов, подчиняющихся деформативной модели h2; E0 - общая асим-
птота функций EK( ) и ES( )
ε(σ)=(β0/EK)σ; S(σ)=[f(K,D)/ES]σ , |
(1) |
и кусочно-линейные или двухпараметрические, подчиняющиеся |
второму |
(обобщенному) закону Гука h2: |
|
ε(σ)=ε0+(β0/E0K)σ; S(σ)=[f(K,D)/E0S](σ–σ0S), |
(2) |
где ε(σ) и S(σ) — соответственно относительная деформация грунта при его компрессионном сжатии в одометре и осадка штампа в грунтовом массиве;
EK=β0[σ/ε(σ)]; ES=f(K,D)[σ/S(σ)]– |
(3) |

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов
гуковские модули деформации, определяемые по закону Гука h1 с использованием данных испытаний соответственно компрессионных и штамповых; ε0 и σ0S — начальные отрезки на осях ε(σ) и σ прямых (2) (рис. 1);
E0K=β0[σ/(ε(σ)–ε0)]; E0S=f(K,D)[(σ–σ0S)/S(σ)] – |
(4) |
модули деформации в обобщенных законах Гука h2; β0 — поправка на отсутствие бокового расширения грунта в одометре при оценке модулей деформации EK и E0K по данным компрессионных испытаний; f(K,D) — функция бокового расширения грунта, формы и размеров штампа [ 1].
Закон Гука h1 лежит в основе модели линейно деформируемой среды [1, 9]. Применим этот закон для определения модуля деформации инженерногеологического элемента (ИГЭ), подчиняющегося обобщенному закону Гука h2. Тогда, подставив в (3) значения ε(σ) и S(σ) по (2), получим функции неустойчивости EK(σ) и ES(σ), отражающие характер изменения гуковских модулей деформации EK и ES в среде h2:
EK(σ)=β0σ/ε(σ)=1/[1/E0K+(ε0/β0)/σ] ; (5) ES(σ)=f(K,D)[σ/S(σ)]=E0S/(1–σ0S/σ) . (6)
а) б)
Рис. 2. а– "гостовский" методопределениякомпрессионногомодулядеформациигрунтов E0K 0 / поугловомукоэффициенту tg / второго(обобщенного) законаГука
h2 – прямойAB, проводимойпокрайнимопытнымточкамкомпрессионнойкривой ( ) без
оценкиначальногоотрезкаε0 наосидеформаций [1]; 1…6 – опытныезначениядавлений
( 1… 6) исоответствующихотносительныхосадокобразца( 1… 6); h1 – первый(прямопропорциональный) законГука– прогнознаяпрямолинейно-деформируемаямодельгеооснования смодулемдеформации E0K 0 tg , определяемымподеформативноймоделиh2; б– «гостов-
ский» методопределения"штампового" модулядеформациигрунтов
E0S f (K , D) / S f (K , D)tg поугловомукоэффициентуtg второго(обобщенного) законаГукаh2 – прямойCD, проводимойпокрайнимопытнымточкамкривойосадкиштампа S( ) безоценкиначальногоотрезка 0S наосидавлений [1]; 1…5 – опытныезначениядавле-
ний( 1… 5) исоответствующихосадокштампа(S1…S5); h1 – первый(прямопропорциональный) законГука– прогнознаяпрямолинейно-деформируемаямодельосадкигеооснованияс модулемдеформации E0S , определяемымподеформативноймоделиh2.

Современные геотехнологии в строительстве и их научно-техническое сопровождение
Функции (5) и (6) стремятся к пределам (рис. 1 ): |
|
|
lim ES ( ) E0S |
const ; lim EK ( ) E0K |
const , |
(7) |
|
|
|
|
равным модулям деформации в обобщенных законах Гука (2). В этой связи необходимо отметить, что методология определения EK и ES как единственных констант однопараметрического закона Гука h1 принципиально отличается от методологии определения E0K и E0S как одних из двух констант двухпараметрического закона Гука h2 [2, 3].
В модели линейно деформируемой среды, составляющей основу современного проектирования, «гостовские» методы определения модулей деформации базируются на аппроксимации нелинейных кривых ε(σ) и S(σ) прямыми в отрезках h2 (рис. 2), а прогноз деформаций осуществляется по закону h1
сиспользованием полученных для h2 модулей E0K или E0S [1]. Такие «комбинации» несовместимых моделей приводят к искусственному изменению прочности и несущей способности геооснований. При компрессии c ростом уплотняющего давления σ сопротивление грунта сжатию принимает две основные формы [6, 7]: может быть постоянным и тогда формируются гуков-
ские прямые h1 или h2, но в большинстве случаев (60-90% из 500 обследованных нами опытов [6, 7]) возрастает, в результате чего темп сжатия грунта уменьшается, формируются выпуклые (по отношению к оси давлений σ) де-
формативные кривые ε(σ) (рис.2) и модуль деформации по Гуку Ek=β0[σ/ε(σ)]
закономерно возрастает с ростом σ (рис. 1). Это обстоятельство определяет отношение проектировщиков к «компрессионным» модулям деформации. При штамповых испытаниях с ростом σ сопротивление грунтового массива напряжениям и сжатию ослабевает и кривые осадки штампов S(σ) становят-
ся вогнутыми (относительно оси давлений, рис. 2) а рассчитываемый по ним гуковский модуль деформации Es=f(K,D)[σ/S(σ)] закономерно уменьшается
сростом σ (рис. 1).
Таким образом, анализ «гостовской» методологии оценки модуля деформации нелинейных сред показывает, что их сопротивление вдавливанию зондов, штампов и фундаментов необходимо определять с использованием законов, максимально точно характеризующих механику данных процессов.
Традиционное применение для этих целей модели линейно деформируемой среды h1 содержит ряд некорректностей, порождаемых несовместимостью законов Гука h1 и h2 с кривыми сжатия ε(σ) и осадки S(σ) грунтов. Очевидно: гуковские модули деформации (3) являются константами только в законе h1. В остальных моделях деформации они становятся функциями неустойчивости, численно равными секущим производным законов деформации – кусоч- но-линейного h2 и нелинейных. Отсюда следует: имея опытные значения данных функций и используя свойства секущих производных [4, 5], легко найти закон деформации. Воспользуемся этой методологией для раскрытия нелинейных закономерностей, широко распространенных при компрессионных и штамповых испытаниях геологической среды [6, 7].

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов
Анализ теоретических подходов к открытию законов нелинейных деформаций показывает на обилие в них некорректностей (особенно в области теории решения обратных задач) и требует введения в методологию изучения данной проблемы приоритета опыта над теорией. Существенным вкладом в развитие этого принципа исследований являются результаты обобщения компрессионных испытаний грунтов Беларуси [6,7]. Они показывают, что гуковские законы h1 и h2 встречаются в 10-40% опытов; в остальных случаях кривые компрессионного сжатия грунтов являются нелинейными и с высокой степенью точности аппроксимируются такими функциями ε(σ), что рассчитываемый по ним гуковский модуль деформации Ek(σ) линейно возрастает с ростом σ (рис. 3):
Рис. 3. Характерные графики компрессионных испытаний 4-х видов грунтов Беларуси: 1 – песок пылеватый (А1); 2 – супесь (В2); 3 – суглинок моренный (С9); 4 – торф
(D7); прямые – E0(σ)=σ/ε(σ); кривые
– ε(σ)=σ/E0(σ); σ, E0(σ) – кг/см2
Ek(σ)=β0[σ/ε(σ)]= Ek* ak , |
(8) |
где Ek* — начальный отрезок прямой Ek(σ); ak [Ek ( ) Ek* ] / const |
— |
угловой коэффициент этой прямой.
Из (8) имеем, что компрессионное сжатие таких грунтов подчиняется нелинейно затухающей функции (модели «nz»):
( ) 0 /(Ek* ak ) 0 /(ak Ek* / ), |
(9) |
асимптота которой max lim ( ) 0 / ak принципиально отличается от сво-
его теоретического аналога εmax = n0 в линейной фазовой модели К.Терцаги [2, 3]; здесь n0 — естественная (до компрессии) пористость грунта.
Используя значения ρd(ε), n(ε) и e(ε) из [3], получаем их деформативные функции для модели «nz» (9):
ρd(σ)=ρd0/[1–ε(σ)]= ρd0/[1–β0/(ak Ek* / )] ; |
|
(10) |
n( ) [n0 ( )]/[1 ( )] |
n |
|
|
|
/(a |
|
E* / ) |
; |
(11) |
|
0 |
|
0 |
|
k |
k |
/ ) |
|
1 0 /(ak Ek* |
|
|
Современные геотехнологии в строительстве и их научно-техническое сопровождение
e( ) e0 0b0 /( ak Ek* / ).
Найдем пределы функций (9)-(12):
lim ( ) lim[ 0 /(ak Ek* / )] 0 / ak k const ;
lim d ( ) d 0 /(1 0 / ak ) d 0 (1 k ) dk const ;
limn( ) (n0 k ) /(1 k ) nk const ;
lime( ) e0 b0 ( 0 / ak ) e0 b0 k ek const .
Компрессионное уплотнение биогенных грунтов может происходить сначала за счет уменьшения объема пор, а затем за счет сжатия минеральных частиц и уменьшения их объема. В этих случаях εk >> ε0 , где ε0 = n0 — предельная деформация (осадка) грунта в линейной фазовой модели [6 ,7]. Тогда из (15) следует, что при
εk>n0→nk<0 и ek=nk/(1–nk)<0. |
(17) |
Таким образом, наличие отрицательных значений у реальных асимптот nk и ek свидетельствует о том, что предельное уплотнение грунта произошло за счет сжатия твердых частиц. Поэтому соотношения (17) могут служить
фазовыми критериями уплотнения грунтов.
Анализ кривых осадок штампов S(σ) в ИГЭ Беларуси показал, что в диапазоне опытных давлений (σ = 1 – 8 кг/см2) при росте σ функция S(σ) растет не с затухающим темпом, как компрессионная ε(σ) в «nz», а, наоборот, с возрастающим (см. графики S(σ) на рис. 4). В результате рассчитываемые по опытным кривым S(σ) гуковские модули деформации (3) становятся равными секущей производной от S(σ) [4, 5,8] и уменьшаются с ростом σ (рис. 1, 4). Очевидно, закон этого уменьшения определяется функцией S(σ). Чтобы установить ее аналитический вид, было апробировано множество нелинейных зависимостей. Оказалось, что только в билогарифмической системе координат ln S(σ) = f (ln σ) опытные кривые S(σ) с высокой степенью точности (с по-
грешностью до 5-10%) аппроксимируются прямой в отрезках (рис. 5): |
|
lnS(σ)=lnS0+λlnσ, |
(18) |
где ln S0 — начальный отрезок прямой (18) на оси осадок штампа ln S(σ); λ — угловой коэффициент этой прямой. В системе координат S = f(σ):
При λ = 1 степенная функция (19) переходит в прямо пропорциональную – закон Гука h1: S(σ)=S0σ.
Таким образом, закон нелинейной деформации, создаваемой вдавливанием штампа в слой грунта, гласит: логарифм осадки штампа ln S(σ) линейно возрастает с ростом логарифма давления на штамп ln σ. Отсюда следует,
что прогноз деформаций должен производиться по параметрам законов этих деформаций: нелинейных – по параметрам нелинейных законов (типа (9)
и(19)), линейных h1 и h2 – по модулям деформаций соответственно (Ek, ES)
и(E0k, E0S). Это значит, что для прогноза нелинейных деформаций надоб-
Раздел 3. Аналитические и численные методы исследований оснований и фундаментов
ность в модулях деформации как констант Гука отпадает. Но поскольку при решении нелинейных задач с неизвестным или предполагаемым законом деформации по-прежнему используются гуковские модули деформации [ 8], найдем их функцию неустойчивости для закона осадки штампов (19):
ES(σ)=f(K,D)[σ/S(σ)]=f(K,D)/S0σλ–1. (20)
Рис. 4. Деформативные кривые осадки штампа S( ) в моренных супесях (графики 8, 11) и суглинке (график 3) и соответствующая динамика гуковского модуля деформации ES f K , D / S в этих слоях. Треугольниками обозначены значения ES, принятые
Геосервисом и определенные по угловым коэффициентам отрезков CD. Геооснование Национальной библиотеки Беларуси (по опытным данным Геосервиса);
3, 8, 11 – номера опытов
В билогарифмической системе координат ln ES(σ) = f (ln σ) степенная функция (20) преобразуется в убывающую прямую (рис. 5):
ln ES ( ) ln E0*S ( 1)ln . |
(21) |
С учетом (21) функция неустойчивости гуковского модуля деформации |
ES(σ) принимает более простой вид: |
|
ES ( ) E0*S 1 . |
(22) |
Из (20) и (21) получаем важное для методологии ИГИ положение: гу-
ковские модули деформации ES(σ), определяемые по данным штамповых испытаний грунтовых толщ, закономерно падают с ростом σ в соответствии с функцией их неустойчивости (22).

Современные геотехнологии в строительстве и их научно-техническое сопровождение
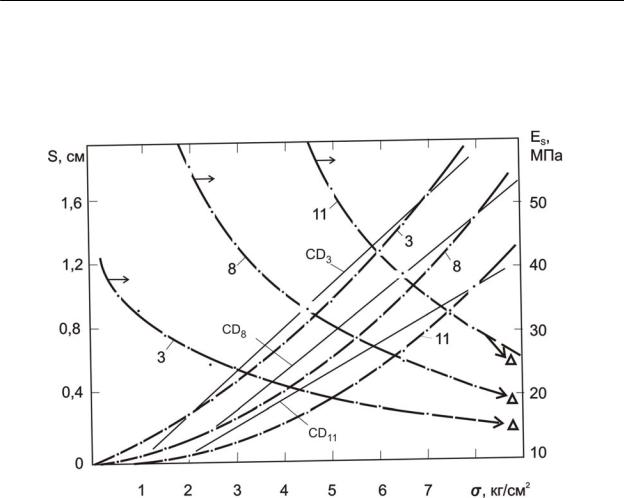
Рис. 5. Примеры использования билогарифмической системы координат для преобразования опытных кривых осадок штампа S(σ) и соответсвющих им функций неустойчивости гуковских модулей
деформации
Es(σ)=f(k,d)[σ/S(σ)] в прямые lnS(σ)=lnS0+λln(σ) и
lnEs(σ)= ln E0*S –(λ–1)lnσ.
Номера графиков означают: опыт 3 – ИГЭ-7, суглинок моренный средней прочности; опыт 8 – ИГЭ–9, супесь моренная, прочная; опыт 11 – ИГЭ-10, супесь моренная, очень прочная. Геооснование Национальной библиотеки Беларуси; S(σ) – см, σ – кг/см2, Es – МПа (по данным Геосер-
виса)
Итак, выполненные исследования указывают на существование следующей фундаментальной закономерности, порождаемой граничными условиями области деформации: если при компрессионном нелинейном сжатии грунта гуковский модуль деформации линейно возрастает с увеличением сжимающего давления σ по закону (8), то при штамповых испытаниях ИГЭ, сложенных тем же грунтом, этот модуль, наоборот, падает с ростом σ по степененному закону (22). Отсюда следует, что линейные законы Гука h1 и h2 имеют место только при абсолютно устойчивых или жестких граничных условиях области уплотнения, исключающих боковое и донное расширение сжимаемого объема грунта; в отличие от линейных, нелинейные законы деформации встречаются в двух случаях: имеют широкое распространение при компрессионных испытаниях (закон (9)) и присущи всем штамповым испытаниям (закон (19)), всегда сопровождаемым боковым и глубинным расширением сжимаемого объёма грунтовой толщи. Это значит, что законы де-
формации одного и того же грунта могут быть самыми различными – как линейными, так и нелинейными – в зависимости от граничных условий области деформации и их устойчивости, т. е. в общем случае законы деформа-

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов
ции грунтов являются функциями граничных условий области их существования. С большой степенью достоверности можно полагать, что данный вывод справедлив для всех законов механики, описывающих аналогичные движения (напр., установившиеся и неустановившиеся фильтрационные потоки) с устойчивыми и неустойчивыми граничными условиями.
Литература
1.Грунты. Методы лабораторного и полевого определения характеристик прочности
идеформируемости: ГОСТ 12248-96. – 64с; ГОСТ 20276-99 – 54с..
2. Костюкович П.Н. Теория взаимосвязей между деформацией уплотнения ε(σ) и сдвиговой прочностью τ(σ) дисперсных грунтов // Геотехника Беларуси : Наука и практика/ Сб. статей Международ. научно-технич. конф. – Минск: БНТУ, 2008. – С.142-162
3.Костюкович П.Н. Деформативные и компрессионные функции сжимаемости грунтов // Геотехника Беларуси : Наука и практика/ Сб. статей Международ. научнотехнич. конф. – Минск: БНТУ, 2008. – С.163-173
4.Костюкович П.Н. Новая методология исследования ускорений силы тяжести // Архитектура. Строительство. Образование: материалы междунар. науч.-практ. конф. – Магнитогорск: Изд-во Магнитогорск. гос. техн. ун-та, 2012. – С.143-152
5.Костюкович П.Н. Исследование ускорений силы тяжести для целей инженерной геологии // Вопросы внедрения норм проектирования и стандартов Европейского Союза в области строительства / Сборник научно-технич. статей. Часть 2. – Минск: БНТУ, 2012 –
С.207-217
6.Костюкович П.Н., Крошнер И.П. Обобщение опытных данных по компрессионным испытаниям грунтов Беларуси // Перспективы развития новых технологий в строительстве и подготовке инженерных кадров Республики Беларусь/ Сб. трудов XV Международ. научно-практич. семинара. Том 2. – Новополоцк, ПГУ, 2008. – С.208-215
7.Костюкович П.Н., Крошнер И.П. Результаты компрессионных испытаний грунтов Беларуси // Журнал «Природные ресурсы». – Минск, 2009, №1. – С.29-34
8.Костюкович П.Н., Крошнер И.П. Теория неустойчивости гуковских модулей деформации, определяемых по данным компрессионных и штамповых испытаний грунтов// Перспективы развития новых технологий в строительстве и подготовке инженерных кадров Республики Беларусь/ Сб. статей XVI Международ. научно-методич. семинара. Часть
2.– Брест, БрГТУ, 2009. – С.168-174
9.Мангушев Р.А., Карлов В.Д., Сахаров И.И. Механика грунтов: Учебник. – М.: Издательство АСВ, 2009. – 214с.
УСТОЙЧИВОСТЬ КОРОТКИХ СВАЙ В ПРОМЕРЗАЮЩИХ ПУЧИНИСТЫХ ГРУНТАХ
Введение
Для индивидуальных домов разработаны конструкции поверхностных теплоизолированных фундаментов (ПТФ) преимущественно для деревянных и других легких жилых домов, которые опирают на экструдированный пенополистирол: он может воспринять нагрузки и одновременно защитить фундамент и дом от промерзания и пучения грунтов.
С конструкциями ПТФ можно познакомиться в брошюре автора [1]. Обычный ПТФ можно сооружать только в теплый период года, чтобы не законсервировать мерзлоту. Но одна из конструкций ПТФ [2] позволяет вести
работы при наличии мерзлоты под
фундаментом (рис. 1).
Если фундамент делается зимой
(например, в декабре, когда слой мерз-
лоты достиг глубины dtf = 70 см), мож-
но выбрать мерзлый грунт на эту глу-
бину dtf и сразу же положить на дно
траншеи или котлована слой пенопласта нужной толщины, сделать насыпку
Рис. 1. Теплоизолированный из непучинистого щебня, а уже по не-
фундамент для строительства зимой: му соорудить собственно поверхност- 1 – фундамент; 2 – щебень; ный малозаглубленный фундамент. 3 – пенопласт; 4 – засыпка; Защищать от дальнейшего промерза-
5 и 6 – теплоизоляция отмостки и пола; 7 – граница промерзания на ния грунт ниже пенопласта будет не
начало работ dtf только сам пенопласт, а также геотермальный поток из земли
Виды коротких свай
В.В. Лушников (Институт УралНИИпроект РААСН,
Современные геотехнологии в строительстве и их научно-техническое сопровождение
УДК 624.151.5: 624.139.6
г. Екатеринбург)
Варсенале строителей имеются показанные на рис.2 и сейчас широко рекламируемые стальные винтовые сваи длиной 1.5-3 м – сваи «Криннер», лопастные сваи «Фундэкс», «Металлист», а также короткие набивные бетонные сваи «ТИСЭ» [3].
Вчастности, сваи «Krinner» появились в Германии, и сейчас они законно и незаконно тиражируются в России. Но в Германии почти нет про-