Сборник трудов конференции СПбГАСУ 2014 ч

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

УДК 624.131.543:51

В.П. Дыба, Е.Г. Скибин (ЮРГПУ, г. Новочеркасск)

АНАЛИТИЧЕСКИЙ РАСЧЕТ НЕСУЩЕЙ СПОСОБНОСТИ ВИСЯЧИХ СВАЙ

В данной статье рассмотрена возможность применения модели критического состояния грунта, разработанной под руководством К. Роско [1] в конце 50-х начале 60-х годов прошлого столетия, для расчета несущей способности висячих свай, работающих, главным образом, за счет сил трения по боковой поверхности. В данной модели грунт переходит в состояние пластического течения при определенном критическом состоянии, которое не зависит от напряженно-деформированного состояния грунта, а только от его вещественного состава.

Авторы стремились удовлетворить требованию продуктивности математической модели. Все параметры и функциональные зависимости модели могут быть получены из отчета инженерно-геологических изысканиях площадки строительства.

Расчет несущей способности свай рассматривается для «влажных» грунтов, т. е. для грунтов переходящих в критическое состояние при уменьшении объема, следовательно, при уменьшении пористости.

Применение модели критического состояния для расчета несущей способности висячих свай обосновано главными достоинствами модели:

прочностные свойства грунта зависят от его текущей плотности;

среди параметров модели нет эмпирически определяемых функций;

нахождение распределения плотности (пористости) в радиальном направлении в зоне уплотнения грунта.

Выше указанные достоинства позволят дать теоретическое решение поставленной задачи для свай, изготавливаемых с вытеснением и извлечением грунта, опираясь только на физико-механические свойства грунта, полученные при стандартных лабораторных испытаниях.

В работах [3], [4] решена одномерная задача о воздействии внутреннего давления на цилиндрическую полость в грунте в рамках модели критического состояния грунта. Получено распределение напряжений и коэффициента пористости в радиальном направлении. Решение данной задачи можно применить к нахождению несущей способности свай.

Несущая способность сваи вычисляется в следующей последовательно-

сти:

1.Нахождение напряжений в грунте в радиальном направлении от

оси сваи.

341

Современные геотехнологии в строительстве и их научно-техническое сопровождение

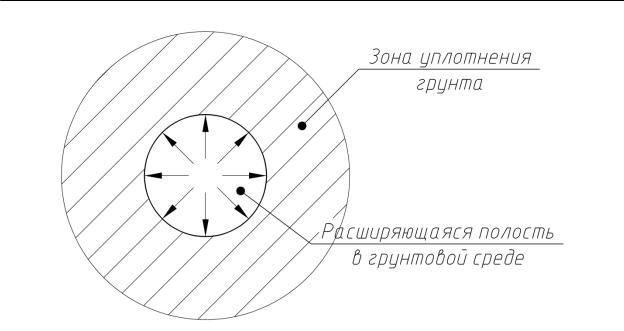
Рис. 1. Уплотненная зона грунта, возникающая при изготовлении сваи с вытеснением грунта.

Математическая модель представляется системой четырех уравнений относительно четырех неизвестных функций, зависящих от радиуса. Решение системы сводится к одному дифференциальному уравнению первого порядка, которое решается численно с помощью стандартной программы Odesolve.

Первое уравнение – уравнение равновесия, второе уравнение – условие прочности, наипростейшее, при котором возможно пластическое течение в условиях компрессии, третье уравнение – следствие логарифического закона компрессии, четвертое уравнение – следствие ассоциированного (нормального) закона текучести.

На рис. 2,3 представлены полученные зависимости по результатам рас-

чета в Mathcad.

342

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

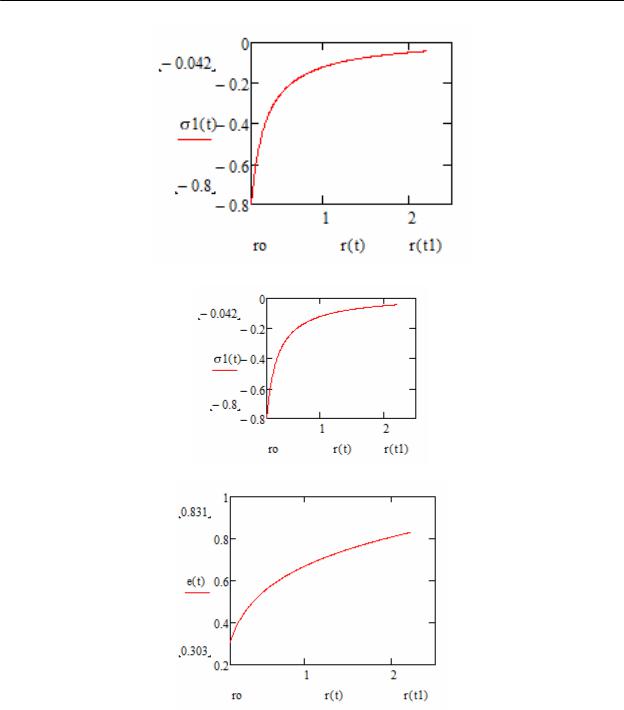
Рис. 2. Зависимость 1-го главного напряжения от радиуса.

Рис. 3. Зависимость 3-го главного напряжения от радиуса.

Рис. 4. Распределение коэффициента пористости

взависимости от радиуса.

2.Нахождение возникающей силы трения при приложении нагрузки на сваю, путем умножения на коэффициент трения давлений действующих на боковую поверхность сваи.

3.Нахождение верхней оценки силы сопротивления под острием сваи, согласно одной из теорем Гвоздева, из равенства мощности внешней силы мощности внутренних сил пластического деформирования.

Этим же способом можно теоретически находить несущую способность фундамента в вытрамбованном котловане [5] и структуру уплотненной зоны вокруг фундамента.

343

Современные геотехнологии в строительстве и их научно-техническое сопровождение

Получающаяся сумма сил трения по боковой поверхности и сил сопротивления под острием сваи будет показывать максимальную нагрузку, которую можно передать на голову сваи, таким образом, мы и получим несущую способность сваи.

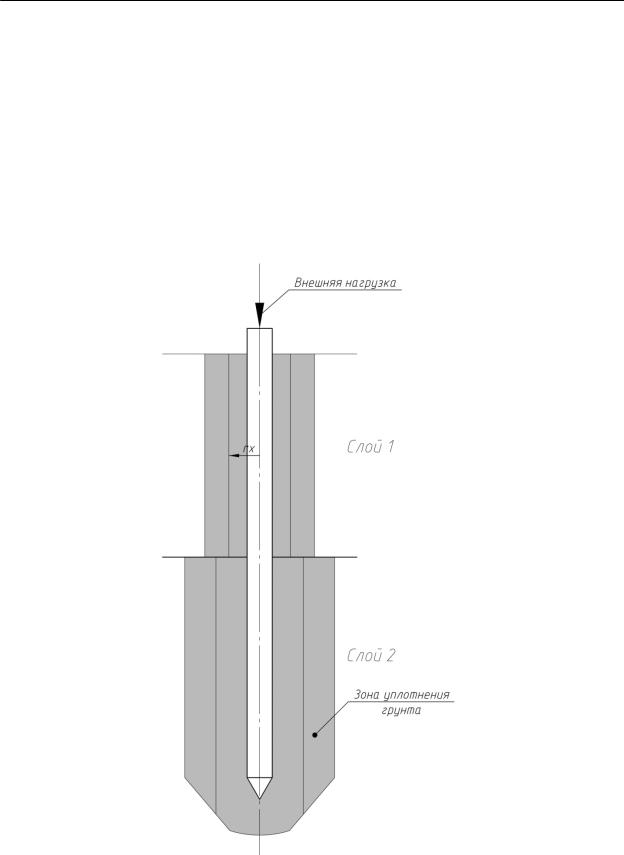
Стоит отметить что свая может потерять несущую способность (по грунту) по следующим поверхностям (рис. 5):

по поверхности соприкосновения грунта и сваи;

на некотором расстоянии rх от оси сваи;

на границе уплотненной зоны с неуплотненным грунтом.

Стоит отметить, что для грунтов с различными физико-механическими характеристиками эти поверхности будут разные.

Рис. 5. Разрез по свае

Стоит отметить, решение данной задачи зависит от принятых параметров модели, таких как уравнения поверхностей нагружения, зависимость ко-

344

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

эффициента пористости от давлений (логарифмический закон уплотнения Терцаги). Таким образом, для различных типов грунтов можно применять и различные параметры модели, вплоть до индивидуальных для каждого грунта, которые можно получить при стандартных лабораторных испытаниях, что позволит получить более точные решения.

Несущая способность сваи, полученная приведенным выше методом, не будет опираться на эмпирические зависимости трудоемких натурных и лотковых испытаний свай, а будет зависеть от прочностных коэффициентов «с» и «φ», от плотности грунта, т. е. характеристик полученных при обычных лабораторных испытаниях, а также принятых закономерностей модели и размера сваи.

Литература

1.Федоровский В.Г. Современные методы описания механических свойств грунтов. Обзор, – М., ВНИИИС, 1985.

2.СП 22.13330.2011 «Основания зданий и сооружений».

3.Дыба В.П., Ширяева М.П. Математическое моделирование пластически уплотняемой грунтовой среды // Численно-аналитические методы: Сборник научных трудов / Юж.-Рос. гос. техн. ун-т. – Новочеркасск: ЮРГТУ, 2007.-С. 101-108.

4.Ширяева М.П. Моделирование процессов пластического деформирования грунтов оснований. Диссертация, – Новочеркасск, 2007. – С. 118.

5.Моргунов В.Н. Экспериментальные исследования работы фундаментов в вытрамбованных котлованах в натурных условиях. // Механика грунтов в геотехнике и фундаментостроении. Всеросийская научно-техническая конференция, г. Новочеркасск:

ЮРГТУ, 2012. – С. 216-224.

6.Дыба В.П., Скибин Е.Г. К теории несущей способности висячих свай. // Международная научная конференция "Инновационные конструкции и технологии в фундаментостроении и геотехнике", г. Липецк, 2013.

УДК 624.131.43

Д.А. Тюрин, А.Л. Невзоров,

(Северный (Арктический) Федеральный университет, г. Архангельск)

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ КОНСОЛИДАЦИИ ТОРФА В ОСНОВАНИИ НАСЫПИ

За несколько последних десятилетий сотрудниками кафедры накоплен значительный объем данных наблюдений за осадкой торфа под пригрузочным слоем песка. Помимо устройства долговременных осадочных марок в пределах городской территории, был оборудован опытный полигон, нивелировка марок на котором осуществляется в течение 18 лет. На рис. 1 представлены графики развития деформаций торфа за этот период [5]. Начальная мощность торфа на участке составляла 6,3…6,7 м.

345

Современные геотехнологии в строительстве и их научно-техническое сопровождение

Рис. 1. График развития деформаций торфа под песчаной пригрузкой: 1 – 9,9 кПа, 2 – 18,7 кПа, 3 – 24,2 кПа, 4 – 26,4 кПа, 5 – 40,7 кПа

Продолжительность консолидации и значение конечной осадки существенно зависят от таких исходных характеристик торфа, как модуль деформации и показатель изменения коэффициента фильтрации, однозначно вычислить которые, пользуясь стандартной методикой, достаточно затруднительно [1]. Поэтому в первую очередь выполнялось численное моделирование компрессионных испытаний.

Исходные свойства образцов торфа: степень разложения 22 %; плотность 0,95…1,05 г/см3; плотность частиц 1,47…1,52 г/см3; степень влажности 0,97…1,00, начальный коэффициент пористости 15,7…18,6 [2].

Нагрузка на образцы прикладывалась в одну ступень. Испытания продолжались до момента достижения условной стабилизации 0,01 мм/сут в течение 19…25 суток. Дренирование поровой влаги было односторонним, как и на опытном полигоне.

Коэффициент фильтрации неуплотненного торфа составлял 3,9 м/сут. К моменту завершения испытаний при нагрузке 12,5 кПа имело место его снижение до 0,29 м/сут, при 25 кПа – до 3,1 10-2 м/сут, а при 50 кПа – до

5,6 10-3 м/сут [3].

Данные испытаний образцов торфа в компрессионно-фильтрационных приборах были использованы при создании численной модели в ПК Plaxis.

Исходными данными для расчета в модели Hardering Soil, кроме физических характеристик торфа, являются следующие показатели: секущий модуль деформации при трехосном нагружении E50, модуль деформации при повторном нагружении Eur, одометрический модуль деформации Eoed, угол

внутреннего трения , удельное сцепление с. В используемой модели важную роль играет коэффициент m, определяющий зависимость модуля деформации от величины напряжений [4]. Помимо этого, задавался также коэффициент Пуассона для разгрузки/последующего нагружения ur. Ранее было установлено [3], что перечисленные выше характеристики отвечают, в первую очередь, за величину конечной осадки.

346

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

Продолжительность консолидации в модели регулируется, главным образом, коэффициентом вертикальной фильтрации ky и показателем изменения коэффициента фильтрации во времени ck.

Для того, чтобы привести модель в соответствие с результатами натурных испытаний, потребовалась оптимизация исходных характеристик грунта. С этой целью был использован один из инструментов Plaxis – «виртуальная лаборатория», позволяющий варьировать исходные параметры в заданных пределах для достижения максимальной сходимости. Особый интерес в данном случае представляли такие показатели, как секущий модуль деформации при трехосном нагружении и модуль деформации при повторном нагружении, поскольку из-за технической сложности трехосных испытаний торфа они не определялись лабораторно. Помимо этого, коэффициент m также был оптимизирован программой.

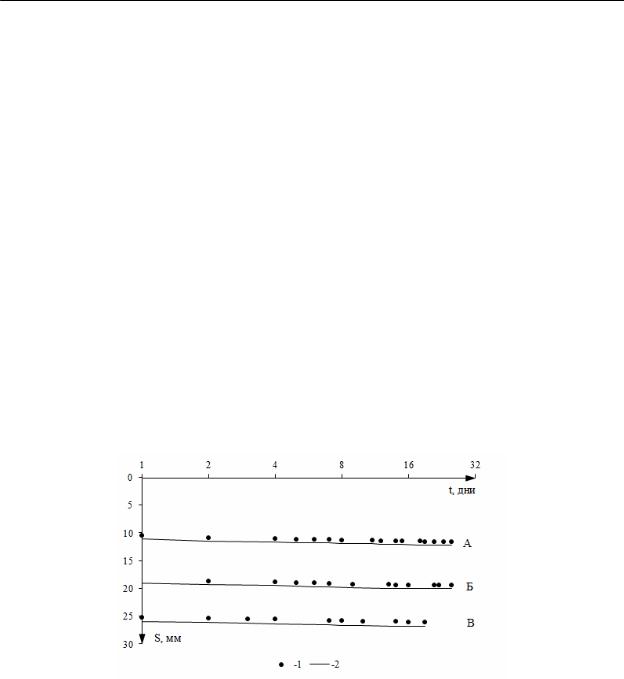
В результате оптимизации были получены такие значения параметров, которые позволили максимально точно воспроизвести компрессионные испытания в численной модели. На рис. 2 сопоставлены данные лабораторных испытаний под нагрузками 12,5…50 кПа и результаты моделирования в логарифмическом масштабе. Хорошая сходимость характерна здесь как для первичной, так и для вторичной консолидации.

Рис. 2. Лабораторные испытания и численная модель

соптимизированными параметрами:

1– лабораторные испытания, 2 – расчетная зависимость

А– 12,5 кПа, Б – 25 кПа, В – 50 кПа.

Следует отдельно отметить, что параметры фильтрации (коэффициент вертикальной фильтрации ky, а также показатель изменения коэффициента фильтрации ck) оптимизировались без использования инструментария виртуальной лаборатории.

По завершении данного этапа работы, полученные значения характеристик грунта были использованы для моделирования осадки торфяного массива в условиях опытного полигона.

347

Современные геотехнологии в строительстве и их научно-техническое сопровождение

Однако полученные результаты оказались неудовлетворительными: фактическое значение осадки на момент последних наблюдений (20 лет с момента начала консолидации) существенно отличалось от численной модели. Программа занижала величину осадки на стадии первичной консолидации (первые 3..5 лет [5]) на величину порядка 0,5 м.

С учетом полученных результатов была избрана иная стратегия моделирования: разделить первичную и вторичную консолидацию по отдельным стадиям расчета с изменением характеристик грунта в точке перехода от первичной консолидации ко вторичной. На основании данных многолетних наблюдений [5], такой переход происходит в среднем через 4 года после начала процесса консолидации.

Таким образом, экспериментальные данные по долговременным осадкам задавались в программу калибровки отдельно для первичной и вторичной консолидации.

Как и предполагалось, наибольшее влияние на конечный результат оказывают такие характеристики, как одометрический модуль деформации Eoed, коэффициент m, учитывающий зависимость модуля деформации от величины напряжений, а также показатель изменения коэффициента фильтра-

ции ck.

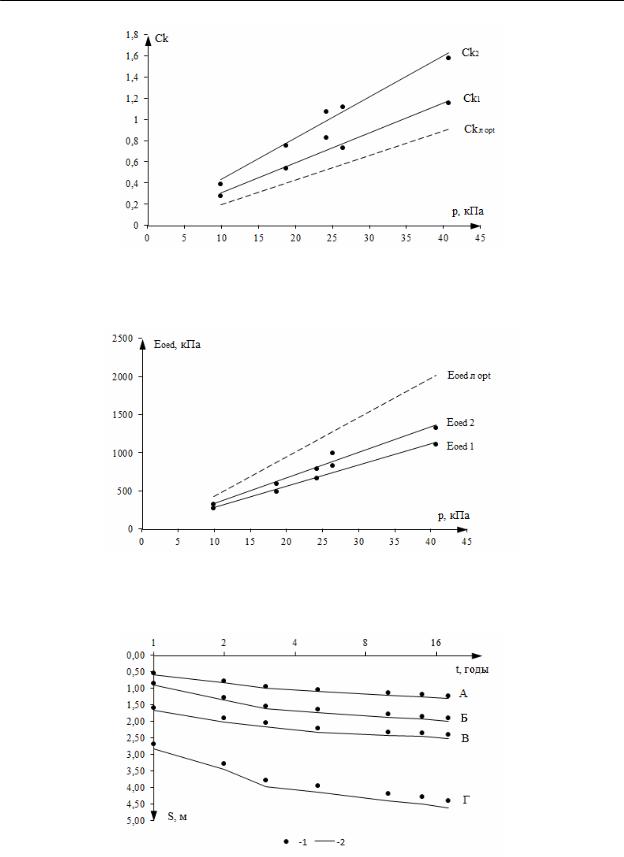
На рис. 3–5 представлены графики зависимостей этих показателей от распределенной нагрузки для каждой стадии консолидации. В этих же координатах представлены оптимизированные графики численного моделирования лабораторных испытаний.

Используя оптимизированные значения для двухстадийного расчета первичной и вторичной консолидации, удалось добиться хорошей сходимости на обеих стадиях. На рисунке 6 представлены результаты расчетов для каждой из нагрузок. Для оси времени был выбран логарифмический масштаб, более наглядно отображающий момент перехода от первичной к вторичной консолидации.

Рис. 3. Линии регрессии для определения показателя m: m1 – для первичной консолидации, m2 – для вторичной,

mл opt – оптимизированное значение по данным лабораторных испытаний

348

Раздел 3. Аналитические и численные методы исследований оснований и фундаментов

Рис. 4. Линии регрессии для определения показателя ck: ck1 – для первичной консолидации, ck2 – для вторичной,

ck л opt – оптимизированное значение по данным лабораторных испытаний

Рис. 5. Линии регрессии для определения Eoed:

Eoed1 – для первичной консолидации, Eoed2 – для вторичной,

Eoed л opt – оптимизированное значение по данным лабораторных испытаний

Рис. 6. Данные многолетних наблюдений и численная модель

соптимизированными параметрами:

1– многолетние наблюдения на полигоне, 2 – численная модель

А– 9,9 кПа, Б – 18,7 кПа, В – 24,2 кПа, Г – 40,7 кПа

349

Современные геотехнологии в строительстве и их научно-техническое сопровождение

Как видим из графиков, хорошая корреляция численной модели с фактическими многолетними наблюдениями характерна для всех рассмотренных нагрузок. Таким образом, двухстадийная модель консолидации позволяет прогнозировать как краткосрочное, так и долгосрочное развитие осадки торфяной залежи с высокой степенью достоверности.

Наличие в ПК Plaxis возможности задавать функциональные взаимозависимости отдельных физико-механических характеристик грунта могло бы помочь добиться хорошей сходимости данных моделирования с натурными наблюдениями при одностадийном расчете. Особенно актуальна эта функция была бы для слабых грунтов, физико-механические свойства которых меняются в процессе консолидации в достаточно широком диапозоне.

Решением проблемы одностадийного расчета консолидации торфа может стать использование как принципиально новых приборов, так и усовершенствованных, с учетом особенностей слабых грунтов. Это позволит получить в лабораторных условиях физико-механические характеристики грунта, адекватно отображающие модель его долговременной осадки. Работа в данном направлении будет являться одним из следующих шагов в создании универсальной численной модели торфяного массива под пригрузкой.

Выводы

1.Калибровка модулей деформации, параметров фильтрации и показателя зависимости деформации от напряжений позволяет с высокой степенью достоверности моделировать компрессионные испытания торфа;

2.Для достижения сходимости результатов прогноза осадки насыпи на торфе с использованием численной модели с данными натурных наблюдений следует производить двухстадийный расчет консолидации – отдельно для первичной и вторичной, с различными характеристиками торфа.

Литература

1.Коновалов П.А. Устройство фундаментов на заторфованных грунтах/ П.А. Коновалов – М., Стройиздат, 1980. – 161 стр.

2.Невзоров А.Л. Город на болоте/ А.Л. Невзоров, А.В. Никитин, А.В. Заручевных – Архангельск, изд-во САФУ, 2012. – 150 стр.

3.Невзоров А.Л., Тюрин Д.А. Численное моделирование компрессионных испытаний торфа. Геотехника: теория и практика. Общероссийская конференция молодых ученых, научных работников и специалистов: межвузовский тематический сборник трудов;

СПбГАСУ. – СПб., 2013. с. 169-173.

4.Brinkgreve R.B.J. PLAXIS 2D Reference Manual [электронный ресурс] / R.B.J. Brinkgreve, E. Engin, W.M. Swolfs – Электрон. текстовые дан. – 2012. Режим доступа: http://www.plaxis.nl/files/files/2D2012-2-Reference.pdf, свободный.

5.Nevzorov A. The long-term peat settlement under the sand embankment. The 5th International Geotechnical Symposium. 22-24 May, 2013. University of Incheon, Republic of Korea. p.403-406.

350