
Левченко 2 часть
.pdfН. Б. ЛЕВЧЕНКО
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
ЧАСТЬ 2
Санкт-Петербург
2001
2
Министерство образования Российской Федерации Санкт-Петербургский государственный архитектурно-строительный университет
Кафедра сопротивления материалов
Н. Б. ЛЕВЧЕНКО
СОПРОТИВЛЕНИЕ МАТЕРИАЛОВ
Учебное пособие по выполнению расчетно-проектировочных работ для студентов всех специальностей и форм обучения
ЧАСТЬ 2
Задачи № 12–24, 26, 27
Под редакцией д-ра техн. наук, проф. В. Д. Харлаба
Санкт-Петербург
2001
3
УДК 539.3/8(07)
Сопротивление материалов: Учебное пособие по выполнению рас- четно-проектировочных работ для студентов всех специальностей и форм обучения. Ч. 2 / Н. Б. Левченко; СПбГАСУ. СПб., 2001. - 110 с.
В пособии даны краткие сведения из теории, необходимые для решения задач, и приводятся примеры решения задач, входящих в расчетно-проектировочные работы, по теме "Изгиб" с подробными объяснениями.
Ил. 55. Табл. 3. Библиогр. 7 назв.
Рецензенты:
д-р техн. наук, проф. В. З. Васильев (Санкт-Петербургский государственный университет путей сообщения); д-р техн. наук, проф. В. В. Улитин (Санкт-Петербургский государст-
венный университет низкотемпературных и пищевых технологий)
Рекомендовано Редакционно-издательским советом СПбГАСУ в качестве учебного пособия
©Н. Б. Левченко, 2001
©Санкт-Петербургский государственный архитектурно-строительный университет, 2001
4
ОБЩИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ РАСЧЕТНОПРОЕКТИРОВОЧНЫХ РАБОТ
Впроцессе изучения курса "Сопротивление материалов" студенты выполняют расчетно-проектировочные работы (РПР). Количество РПР и задач, входящих в каждую из этих работ, зависит от специальности и количества часов, отведенных в учебном плане на изучение курса. Цель РПР – сознательное усвоение теоретического курса и приобретение навыков решения задач, имеющих как академический, так и практический характер.
Данное учебное пособие предназначено для оказания помощи студентам при выполнении расчетно-проектировочных работ. Номера задач, решение которых объясняется в данном пособии, соответствуют номерам задач в методических указаниях [4], по которым студенты выбирают схемы решаемых задач.
Вданном пособии приводятся краткие теоретические сведения и основные формулы, необходимые для выполнения задач, объясняются смысл и порядок решения задач. Решение одних задач сопровождается численными расчетами, решение других приведено в общем виде. Ни в коем случае не следует копировать решение задач, не разобравшись со смыслом того, что вы делаете. Пособие не заменяет учебник, поэтому перед выполнением задач прочитайте те разделы учебников, которые приведены в перечне литературы по изучаемой теме. В процессе расчетов обращайте внимание на единицы измерения величин, входящих в формулы. Не забывайте писать, в каких единицах Вы получили результат. Рекомендуемые единицы измерения приведены в перечне используемых обозначений. Все арифметические вычисления следует выполнять с точностью до трех значащих цифр – точностью, достаточной для инженерных расчетов.
Расчетно-проектировочные работы оформляются на стандартных листах писчей бумаги формата А-4 (210х297). Перед решением задачи необходимо нарисовать расчетную схему задачи в масштабе в соответствии со своими данными. Решение задачи должно сопровождаться короткими пояснениями, рисунки желательно делать карандашом, на листах должны быть оставлены поля для замечаний препода-
5
вателя. После выполнения всех задач, входящих в расчетнопроектировочную работу, листы с решением следует сброшюровать и снабдить титульным листом.
ИСПОЛЬЗУЕМЫЕ ОБОЗНАЧЕНИЯ
Нагрузки:
F – сосредоточенная сила, кН;
M – сосредоточенная пара сил (момент), кН м;
q – интенсивность распределенной по длине стержня нагрузки, кН/м.
Обозначение осей:
x – продольная ось стержня;
y, z – главные центральные оси инерции поперечного сечения стержня.
Геометрические характеристики поперечного сечения стержня:
A – площадь поперечного сечения, см2;
Sy, Sz – статические моменты относительно осей y, z, см3;
Iy, Iz – осевые моменты инерции относительно осей y, z, см4; Ip– полярный момент инерции, см4.
Внутренние усилия:
N – продольная сила, кН;
Qy , Qz , (Q) – поперечные силы, кН;
My , Mz, (M) – изгибающие моменты кН м; Mк – крутящий момент, кН м.
Напряжения:
σx , σy , σz , (σ) – нормальные напряжения, МПа; τxy , τyz , τzx , (τ) – касательные напряжения, МПа; σ1, σ2 , σ3 , (σгл) – главные напряжения, МПа.
Деформации и перемещения:
εx , εy , εz , (ε) – относительные продольные деформации; γxy , γyz , γzx , (γ) – угловые деформации (углы сдвига);
∆l – абсолютная деформация стержня при растяжении-сжатии (перемещение точек оси вдоль оси x), см;
v, w – прогибы оси стержня (балки) при изгибе (перемещения точек оси вдоль осей y, z), см;
ϕ – угол поворота оси стержня (балки) при изгибе, рад; θ – угол закручивания стержня (вала) при кручении, рад.
6
Характеристики материала:
σпц – предел пропорциональности, МПа; σт – предел текучести, МПа;
σв – временное сопротивление (для хрупких материалов σрв– предел прочности при растяжении, σсв– предел прочности при сжатии), МПа;
[σ], [τ] – допускаемые напряжения, МПа; E – модуль упругости, МПа;
ν– коэффициент Пуассона;
α– коэффициент линейного температурного расширения, 1/град.
7
4. ИЗГИБ
Основные понятия и формулы
Изгиб – такой вид деформации стержня, при котором его ось искривляется. Стержень, подверженный изгибу, называется балкой. Конструкция, состоящая из нескольких изгибаемых стержней, соединенных между собой чаще всего под углом 90°, называется рамой. В данном разделе рассматриваются балки и рамы, подверженные плоскому поперечному изгибу. В этом случае вся нагрузка приложена перпендикулярно оси стержня в одной плоскости, совпадающей с плоскостью симметрии поперечного сечения; изогнутая ось является плоской кривой. При плоском поперечном изгибе в балке возникают два вида внутренних усилий: поперечная сила Q и изгибающий момент M. В раме при плоском поперечном изгибе возникают три усилия: продольная N, поперечная Q силы и изгибающий момент M.
Правила знаков для поперечной силы и изгибающего момента зависят от вида рассматриваемой конструкции (прямолинейная балка, рама, криволинейный стержень) и приведены в соответствующих разделах.
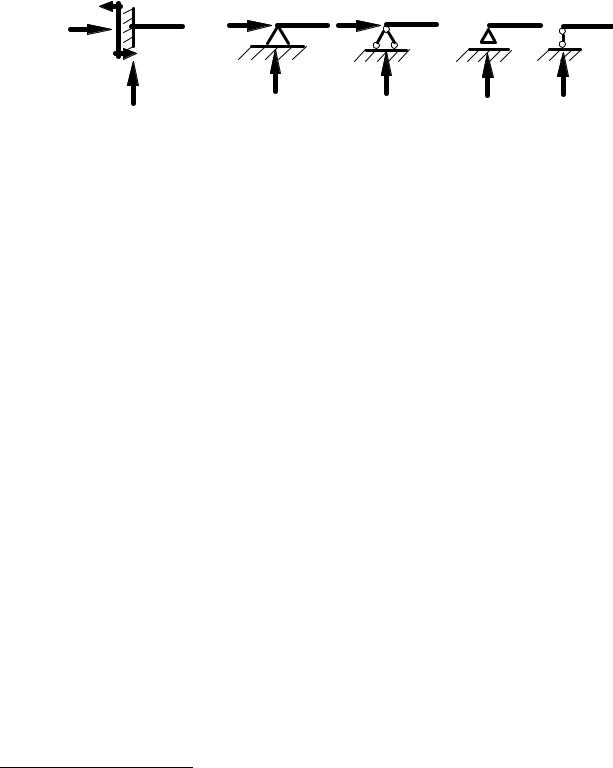
Перед тем, как использовать метод сечений для определения внутренних усилий, как правило, надо найти опорные реакции, возникающие в закреплении стержня. Если опорные реакции и внутренние усилия можно найти из уравнений статики, то конструкция называется статически определимой. Чаще всего мы встречаемся с тремя видами опорных закреплений стержней: жестким защемлением (заделкой), шарнирно-неподвижной опорой и шарнирно-подвижной опорой. На рис. 4.1 показаны эти закрепления. Для неподвижной (рис 4.1, б) и подвижной (рис. 4.1, в) опор приведены два эквивалентных обозначения этих закреплений. Напомним, что при действии нагрузки в одной плоскости в заделке возникают три опорных реакции (вертикальная, горизонтальная реакции и сосредоточенный реактивный момент) (рис. 4.1, а); в шарнирно-неподвижной опоре – две реак-
8
а МА |
б |
|
|
в |
|
|
А |
А |
А |
А |
А |
HA |
HA |
|
HA |
|
|
|
RA |
RA |
RA |
RA |
RA |
Рис. 4.1. Опорные реакции:
а– в заделке; б – в шарнирно-неподвижной опоре;
в– в шарнирно-подвижной опоре
тивные силы (рис. 4.1, б); в шарнирно-подвижной опоре – одна реакция – сила, перпендикулярная плоскости опирания (рис. 4.1, в).
После определения опорных реакций внутренние усилия в статически определимых конструкциях определяем с помощью метода сечений. Подробно процесс определения внутренних усилий рассматривается при решении конкретных задач.
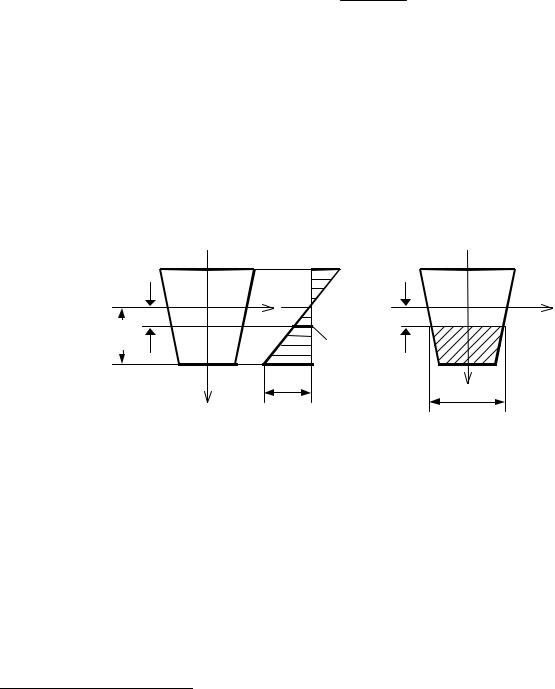
Когда внутренние усилия найдены, можно определить напряжения в поперечном сечении изгибаемого стержня. В произвольной точке поперечного сечения возникают нормальное и касательное напряжения, которые для прямолинейных стержней находятся следующим образом:
• нормальные напряжения в балке определяются по формуле1
σx = σ = |
Mz , |
(4.1) |
|
I y |
|
где М – величина изгибающего момента в рассматриваемом сечении; z – координата той точки поперечного сечения, в которой определяется σ, в главной центральной системе координат; I y – осевой момент
инерции относительно главной центральной оси y. Распределение нормальных напряжений по высоте сечения показано на рис. 4.2, а. Ось y, на которой нормальные напряжения равны нулю, называется нейтральной осью;
1 В рамах при наличии продольной силы к нормальным напряжениям добавляется слагаемое N A.
A.
9
• касательные напряжения определяются по формуле Журавско-
го2:
QS o (z)
τxz = τ = y . (4.2)
I yb(z)
В формуле Журавского Q – значение поперечной силы в рассматриваемом сечении; S oy (z) – статический момент отсеченной части сече-
ния, зависящий от того, в какой точке определяется касательное напряжение; b(z) – ширина сечения на уровне точки, в которой находится напряжение. Например, на рис. 4.2, б заштрихована отсеченная часть сечения и показана ширина b(z) при определении касательных напряжений в точках, удаленных от оси y на расстояние z.
а |
|
б |
|
|
|
|
z |
y |
Mz z |
y |
zmax |
σ = |
|
||
|
|
I y |
z |
|
|
z |
σmax |
|
|
|
Эпюра σ |
|
b(z) |
|
|
|
|
|
Рис. 4.2. К определению напряжений при изгибе:
а– распределение нормальных напряжений по высоте балки;
б– определение отсеченной части сечения в формуле Журавского
Из формулы (4.1) следует, что максимальные нормальные напряжения действуют в точках, наиболее удаленных от оси y (нейтральной оси). Для определения максимальных напряжений из формулы (4.1) можно получить
2 Заметим, что формула Журавского для стержней массивного поперечного сечения дает величину не полного касательного напряжения τx, а его проекции на ось z (τxz). Для тонкостенных стержней (двутавр, швеллер) по формуле Журавского можно найти полное касательное напряжение τx в любой точке поперечного сечения.

10 |
|
|
|
|
|
|
σmax = |
|
M |
|
|
, |
(4.3) |
|
|
|||||
|
|
|
|
|||
|
|
|
|
|||
|
Wy |
|
||||
где Wy = I y zmax – момент сопротивления балки при изгибе. Для
балок круглого и прямоугольного сечений моменты инерции и моменты сопротивления находятся по формулам
Ο |
|
|
πr 4 |
|
I y = |
|
bh3 |
|
|
|
||||
I y |
= |
|
|
; |
|
|
|
|
; |
|
(4.4) |
|||
|
4 |
12 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
|
Ο |
|
|
πr3 |
|
|
|
|
bh |
2 |
|
|
||
Wy |
= |
|
; |
Wy |
= |
|
|
|
|
. |
(4.5) |
|||
4 |
|
6 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Закон распределения касательных напряжений, определяемых по формуле Журавского, зависит от формы поперечного сечения. Для балок круглого и прямоугольного сечений касательные напряжения изменяются по высоте балок по закону квадратной параболы (рис. 4.3, а). Они равны нулю в точках, наиболее удаленных от нейтральной оси y, и максимальны в точках, лежащих на оси y. Из формулы (4.2) для балок круглого и прямоугольного сечений следуют формулы для определения максимальных касательных напряжений
τΟmax = |
4 |
|
Q |
; |
τmax = |
3 |
|
Q |
. |
(4.6) |
3 |
|
A |
|
|
||||||
|
|
|
|
2 A |
|
|||||
Очень часто употребляемым сечением для балок является двутавр. Касательные напряжения в полках и стенках двутавровой балки распределяются по разным законам. Наиболее важными при проверке прочности являются касательные напряжения в стенке двутавра. На рис. 4.3, б показана эпюра распределения касательных напряжений в стенке двутавра. Максимальные касательные напряжения в двутавровой балке так же, как и в балках круглого и прямоугольного сечений, действуют в точках, лежащих на нейтральной оси y. Об определении касательных напряжений в двутавре подробно будет сказано при решении задачи о проверке прочности двутавровой балки.
