

ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНИЮ
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ АРХИТЕКТУРНО-СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ
Факультет автомобильно-дорожный
Кафедра Транспортно-технологических машин и оборудования
Дисциплина: автомобильные двигатели
Курсовой проект по автомобильным двигателям
«Кинематическое и динамическое исследование машины с кривошипно-ползунным механизмом»
(Компрессор 1-цилиндровый двойного действия)
Выполнил студент группы АХ-3 Бочкарев Д. А. _______________
Проект защищен с оценкой: _______________________________
Доцент кафедры Степанов В. Н. _________________________
СПб 2011
Содержание
Содержание…………………………………………………………………………………..2
Кинематический расчет кшм
Кинематические параметры центрального КШМ:
S – ход поршня (92,8 мм);
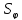 –путь
поршня
–путь
поршня
– угол поворота коленчатого вала;
- угол отклонения оси шатуна от оси цилиндра;
R
– радиус кривошипа ( 28
мм);
28
мм);
 –длина
шатуна;
–длина
шатуна;
 –отношение
радиуса кривошипа к длине шатуна;
–отношение
радиуса кривошипа к длине шатуна;
 п
– угловая скорость вращения коленчатого
вала.
п
– угловая скорость вращения коленчатого
вала.
Задача кинематического расчета – нахождение перемещений, скоростей и ускорений в зависимости от угла поворота коленчатого вала. На основе кинематического расчета проводятся динамический расчет и уравновешивание двигателя.
Перемещение поршня:
 шаг
15.
шаг
15.
 ,
данные в таблицу [2].
,
данные в таблицу [2].
Скорость поршня:
 ,
данные в таблицу [2].
,
данные в таблицу [2].
Ускорение поршня:
 ,
данные в таблицу [2].
,
данные в таблицу [2].
Динамический расчет КШМ
Приведение масс деталей КШМ:
Приведение масс деталей поршневой группы:
Конструктивная масса поршневой группы:
 ;
;
масса поршневой группы (массы собственно поршня, поршневых колец, поршневого пальца и заглушки):
 .
.
Конструктивная масса шатуна:
 ;
;
Масса шатуна:
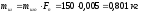 .
.
Длина шатуна:
 ,
принимаем
,
принимаем .
.
Зная длину шатуна определяем длину от оси верхней головки шатуна до центра тяжести:
 ,
принимаем
,
принимаем
 .
.
Масса шатуна, приведенная к оси шейки коленчатого вала:
 кг
кг
Масса шатуна, приведенная к оси поршневого пальца

Конструктивная масса колена:

Масса кривошипа:
 ,
,
Масса, приведенная к оси шатунной шейки:

Масса, приведенная к оси поршневого пальца

Эквивалентная схема кшм:
Силы и моменты, действующие в КШМ:
Силы инерции:
Сила инерции поступательно движущихся масс:
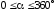 шаг
15.
шаг
15.
 ,
данные в таблицу [2].
,
данные в таблицу [2].
Суммарная сила, кН, приложенная к центру поршневого пальца может быть рассчитана по выражению:

При
этом значения
 берутся непосредственно из развернутой
диаграммы удельной результирующей
силы, приложенной к центру поршневого
пальца.
берутся непосредственно из развернутой
диаграммы удельной результирующей
силы, приложенной к центру поршневого
пальца.
Сила инерции вращающихся масс:
 .
.
Сила приложена в центре шатунной шейки, постоянна по величине и направлению и направлена по радиусу кривошипа.
Силы давления газов:
Силы давления газов в цилиндре двигателя в зависимости от хода поршня определяются по индикаторной диаграмме, построенной по данным теплового расчета.
Сила давления газов на поршень действует по оси цилиндра:
 ,
где
,
где
 –давление
газов в цилиндре двигателя, определяемое
для соответствующего положения поршня
по индикаторной диаграмме;
–давление
газов в цилиндре двигателя, определяемое
для соответствующего положения поршня
по индикаторной диаграмме;
 –давление
в картере;
–давление
в картере;
Результаты заносим в таблицу.
Сила нормального давления поршня на зеркало цилиндра:

Сила, действующая вдоль оси шатуна:
 ,
где
,
где
 –угол
наклона шатуна относительно оси цилиндра.
–угол
наклона шатуна относительно оси цилиндра.

Перенеся
силу
 по линии её действия
в центр шатунной шейки, можно разложить
эту силу на две составляющие:
по линии её действия
в центр шатунной шейки, можно разложить
эту силу на две составляющие:
Сила, действующая вдоль кривошипа (радиальная составляющая):
 .
.
Сила, создающая крутящий момент (тангенсальная составляющая):
 .
.
Сила Т в плече R создает крутящий момент относительно оси КВ:
 .
.
Вычисляем силы и моменты, действующие в КШМ через каждые 15 поворота кривошипа. Результаты вычислений заносим в таблицу [3], строим графики сил и моментов.
Опрокидывающий момент:
Сила нормального давления поршня на зеркало цилиндра создает относительно оси КВ опрокидывающий момент, который вызывает в опорах двигателя реакции.

Т.
к.
 ,
то
,
то

Уравновешивание двигателя
В уравновешенном двигателе при установившемся режиме работы силы и моменты сил, передаваемые на его опоры, постоянны по величине и направлению или равны нулю.
Уравновешивание можно осуществить двумя способами:
расположение определенным образом цилиндров и выбором такой кривошипной системы коленчатого вала, чтобы переменные силы инерции и их моменты взаимно уравновешивались;
созданием с помощью дополнительных масс (противовесов) новых сил, в любой момент времени равных по величине, но противоположных по направлению основным уравновешиваемым силам.
Динамический расчёт показывает, что на КШМ действуют:
-
силы инерции поступательно движущихся
масс
 и
и ,
,
-
центробежные силы инерции
 ,
,
-
возникают моменты
 ,
, ,
, ,
, .
.
Все эти силы и моменты вызывают неуравновешенность двигателя.
Следует учитывать, что опрокидывающий (крутящий) момент уравновесить невозможно, так как двигатель имеет один коленчатый вал. Следовательно, считаем двигатель уравновешенным, если выполняются следующие условия:
 =0,
=0,
 =0,
=0,
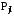 =0,
=0,
 =0,
=0,
 =0,
=0,
 =0.
=0.
Для двухтактного двухцилиндрового рядного двигателя с кривошипами под углом 180 имеем:
 ;
;

 .
.
Уравновешивание оставшихся сил и моментов:
1) Силы инерции второго порядка обоих цилиндров всегда имеют взаимно одинаковое направление и поэтому не уравновешиваются, а дают свободную силу:

или
 .
.
Эта сила действует по оси параллельной осям цилиндров и проходящей через середину коленчатого вала, и может быть уравновешена только противовесами, установленными на дополнительных валах, вращающихся навстречу друг другу с угловой скоростью 2:
радиус
вала принимаем
 ;
;
Масса противовеса рассчитывается из условия:
 ;
;
где
 л
– сила, возникающая при вращении
уравновешивающего вала;
л
– сила, возникающая при вращении
уравновешивающего вала;
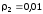 –диаметр
уравновешивающего вала;
–диаметр
уравновешивающего вала;
 кг
– масса противовеса на уравновешивающем
валу.
кг
– масса противовеса на уравновешивающем
валу.
2) Неуравновешенный момент от сил инерции первого порядка вызывает продольные колебания двигателя. Уравновесим этот момент установкой двух валов с противовесами, вращающимися в разные стороны с угловой скоростью .

Момент на одном уравновешивающем валу будет равен:
 ,где
,где
 м
– радиус уравновешивающего вала;
м
– радиус уравновешивающего вала;
 м
- длина уравновешивающего вала.
м
- длина уравновешивающего вала.
Общую массу вала находим из:

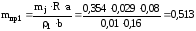 кг,
кг,
так как масса на валу распределена по его концам на две равные части, то каждая из них равна:
 кг.
кг.
3) Величина момента от центробежных сил инерции, действующего во вращающей плоскости коленчатого вала:
 .
.
Этот
момент может быть полностью уравновешен
установкой противовесов с массой
 на продолжении щек коленвала.
на продолжении щек коленвала.
Масса
 ,
расположенная на расстоянии
,
расположенная на расстоянии от оси коленчатого вала, определяется
аналогично предыдущему:
от оси коленчатого вала, определяется
аналогично предыдущему:

откуда
 кг.
кг.
