2.4. Применение частотного метода к исследованию динамики нелинейных сау

Частотный метод применяется довольно широко как для исследования периодических режимов (автоколебаний), так и для переходных процессов в нелинейных системах. Для исследования автоколебаний (возможности их возникновения, их амплитуды и частоты) в сложных нелинейных системах часто применяется метод гармонического баланса [7, 11, 17], основанный на гармонической линеаризации существенно нелинейных характеристик звеньев САУ. Данный метод является приближенным, поскольку учитывает только первую гармонику на выходе нелинейного звена (НЗ), однако применение метода дает тем меньшую погрешность, чем сложнее система, т.е. чем больше инерционных звеньев она имеет. Метод гармонического баланса применяется как при наличии одного НЗ, так и нескольких НЗ, разделенных линейными инерционными звеньями [11, 12]. Метод позволяет с помощью коррекции частотных характеристик линейной части системы устранять или в случае необходимости вводить режим автоколебаний.

Как известно, при исследовании методом гармонического баланса система представляется, состоящий из линейной части с амплитудно-фазовой характеристикой (АФХ) W_л(j) и нелинейного звена с АФХ J(A), где А – амплитуда первой гармоники на входе НЗ. Между обеими комплексными характеристиками есть известная аналогия:

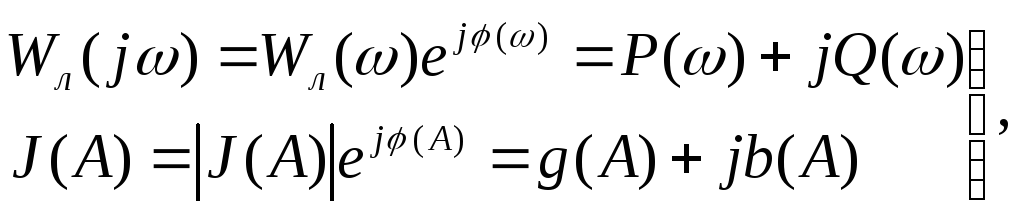(2.12)

т.е. они могут быть представлены как в виде амплитудных и фазовых, так и в виде вещественных и мнимых характеристик. В последнем случае составляющие g(A) и b(A) называются коэффициентами гармонической линеаризации НЗ. Вместе с тем между характеристиками W_л(j) и J(A) есть и существенные различия, т.к. W_л(j)=f(), но f(А), а J(A)=f(A), но f().

При исследовании динамики САУ, как правило, приходится иметь дело с типовыми НЗ, для которых известны J(A) или g(A) и b(A). Интересно отметить, что поскольку b(A)=s/A², где s- площадь петли неоднозначной нелинейной характеристики, то для однозначных нелинейностей J(A)=g(A). Для удобства расчетов и создания типовых графиков коэффициентов гармонической линеаризации используют обычно не J(A), а нормированную амплитудную характеристику:

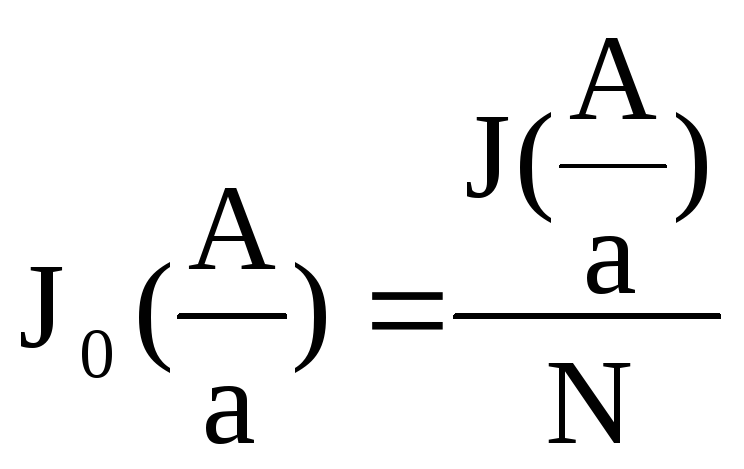, (2.13)

или нормированную обратную характеристику:

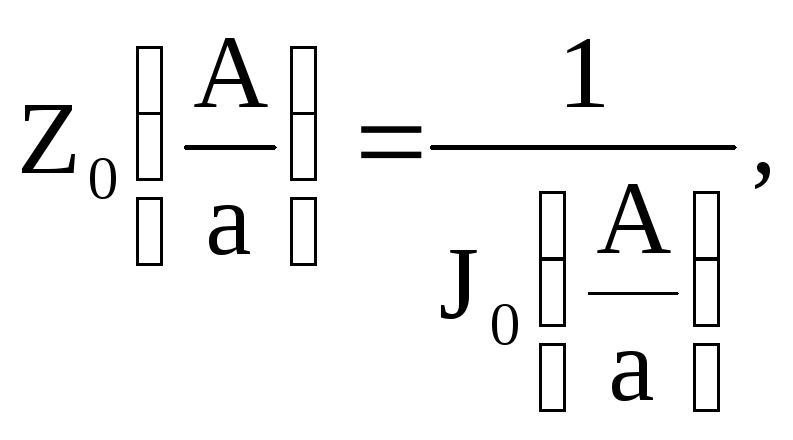(2.14)

где а, N=(В/а) – параметры статической характеристики НЗ.

Рассмотрим некоторые примеры НЗ, их амплитудные характеристики и раскроем физический смысл этих характеристик.

На рис. 2.7,а представлена нелинейная статическая характеристика звена типа «ограничение», довольно часто встречающегося в системах электропривода (ограничение выходного напряжения регуляторов, тиристорного преобразователя и др.). На рис. 2.7,б показаны соответствующие амплитудные характеристики звена и . Физически есть отношение амплитуды 1-й гармоники на выходе НЗ А_вых1 к амплитуде А входной синусоиды, причем для однозначных нелинейностей фазовая характеристика При подаче на вход рассматриваемого звена синусоиды с амплитудой Аа отсутствует искажение сигнала на выходе, а при Аа звено ограничивает сигнал на выходе во все большей степени по отношению к амплитуде А входного сигнала. Это и отражено спадающей кривой . При этом обратная амплитудная характеристика , представляющая собой отношение амплитуд сигналов входа к выходу, будет возрастать, стремясь к бесконечности при. На рис. 2.7,в изображена амплитудная характеристика 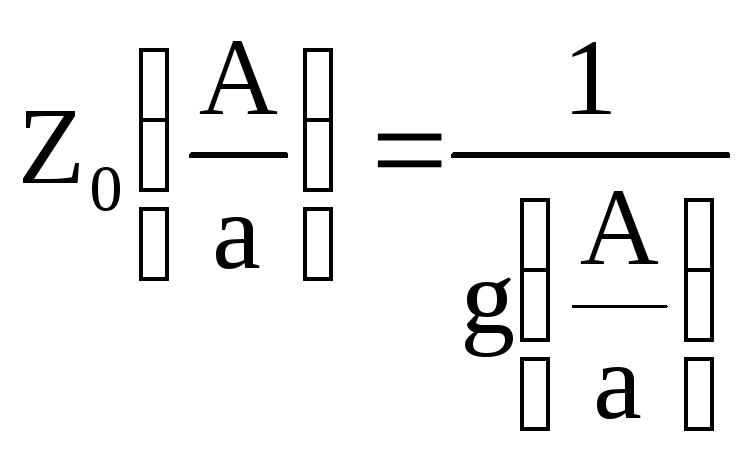рассматриваемого звена в логарифмическом масштабе. Характеристика начинается от значения=1, поскольку при 0<1 . Применение логарифмических характеристик при исследовании нелинейных систем дает те же преимущества, что и в линейных системах. В частности, амплитудные характеристики типовых нелинейных звеньев приобретают стандартный вид и могут быть представлены в виде шаблонов.

Рассмотрим теперь НЗ «зона нечувствительности», статическая характеристика которого приведена на рис. 2.8,а для случая симметричного (сплошная линия) и несимметричного (пунктирная линия) расположения. Таким звеном, в частности, может быть аппроксимирован зазор в механических передачах в ненагруженном (при моменте сопротивления М_с=0) и нагруженном состоянии. На рис. 2.8,б представлены соответствующие амплитудные характеристики звена и , полученные на основе физических представлений, описанных для предыдущего НЗ. На рис. 2.8,в изображены логарифмические характеристики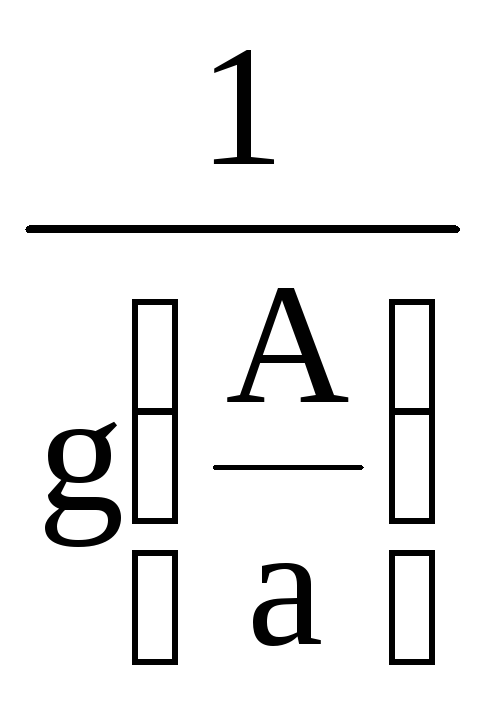рассматриваемого звена – зазора, ненагруженного и нагруженного в различной степени моментом М_с. Характеристики построены на основании рис.2.7,б для относительных значений _с/а.

Путем аналогичных рассуждений могут быть получены амплитудные характеристики и других НЗ как с однозначными, так и с петлевыми статическими характеристиками [11, 12], причем у неоднозначных нелинейностей, кроме амплитудной, будет еще и фазовая характеристика, характеризующая сдвиг по фазе 1-й гармоники выходного сигнала НЗ относительно входной синусоиды.

Рассмотрим применение метода гармонического баланса к исследованию автоколебаний в САУ с одним нелинейным звеном. При этом структурная схема САУ преобразуется к виду, показанному на рис. 2.9, где W_л(р) – передаточная функция линейной части системы.

Переходя от W_л(р) к W_л(j), можно на основании данной структуры записать следующие уравнения в комплексной форме

(2.15)

(2.16)

Найдя из уравнения (2.15) и подставляя в (2.16), имеем:

(2.17)

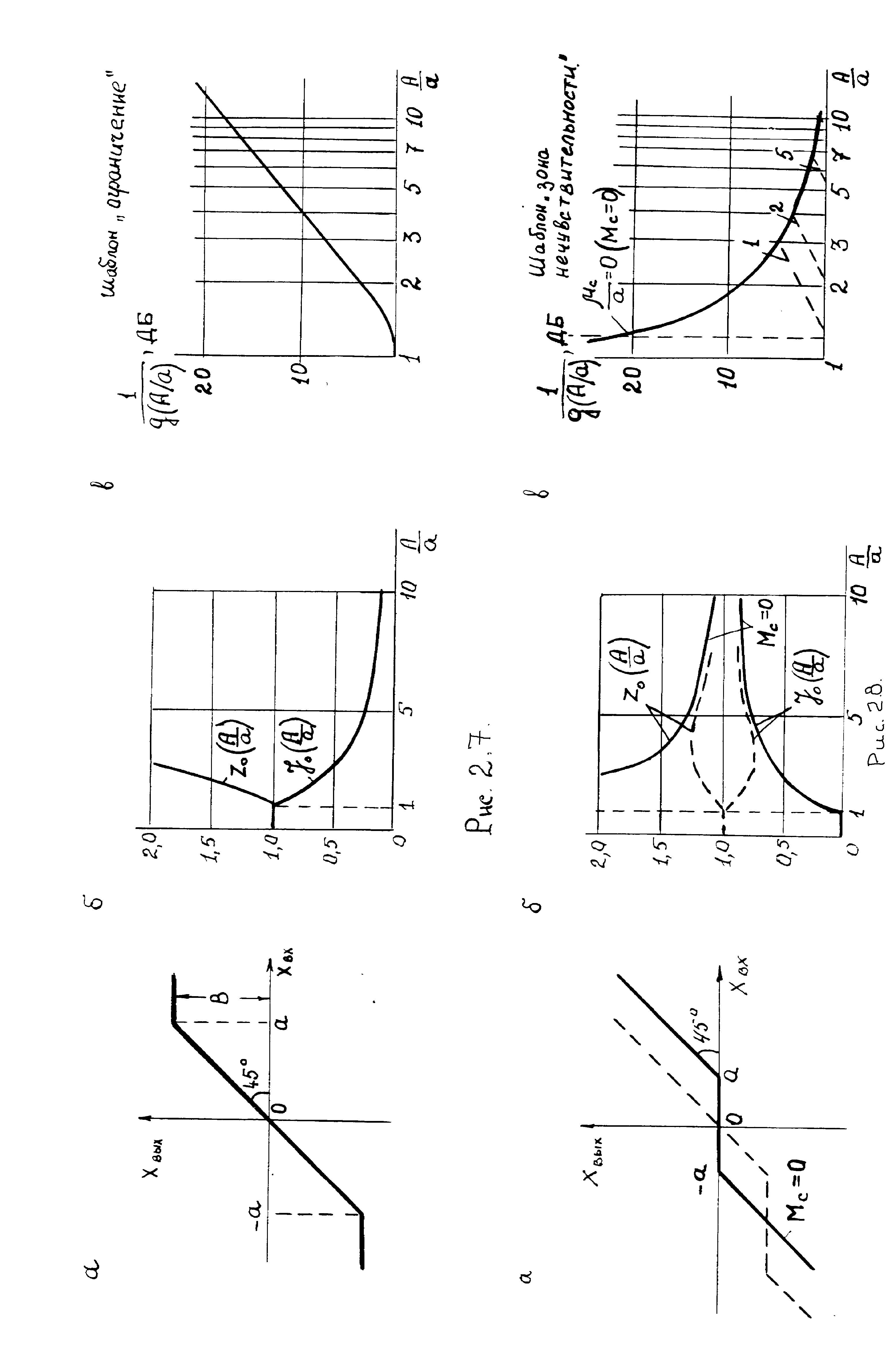
Откуда уравнение гармонического баланса будет:

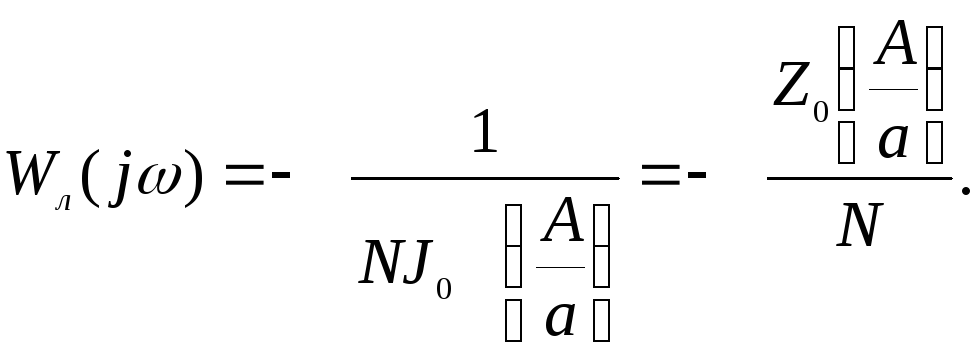(2.18)

Последнее уравнение решается графически.

П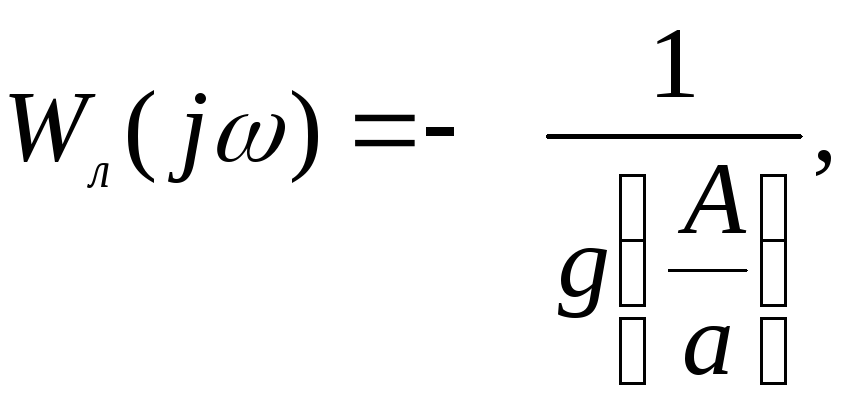рименительно к системе с НЗ типа «ограничение» уравнение гармонического баланса примет вид:

(2.19)

поскольку при симметричном расположении статической характеристики НЗ (см. рис. 2.7,а) N=1. На рис. 2.10,а представлены соответствующие характеристики линейной части и нелинейного звена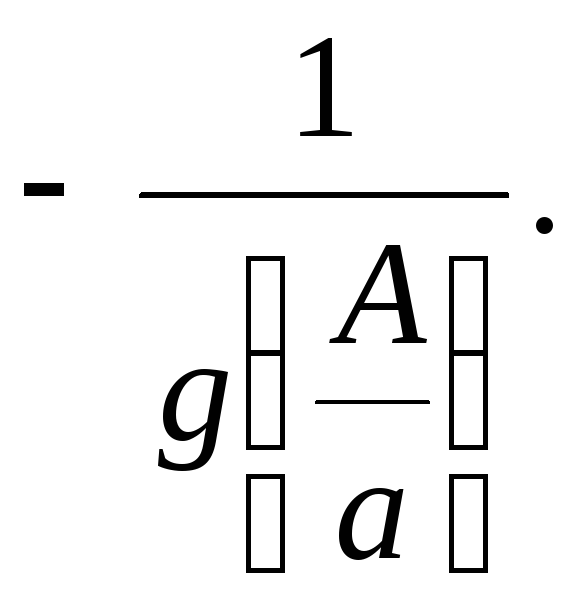АФХохватывает точку с координатами –1,j0, что говорит о неустойчивости линейной системы. Амплитудная характеристика 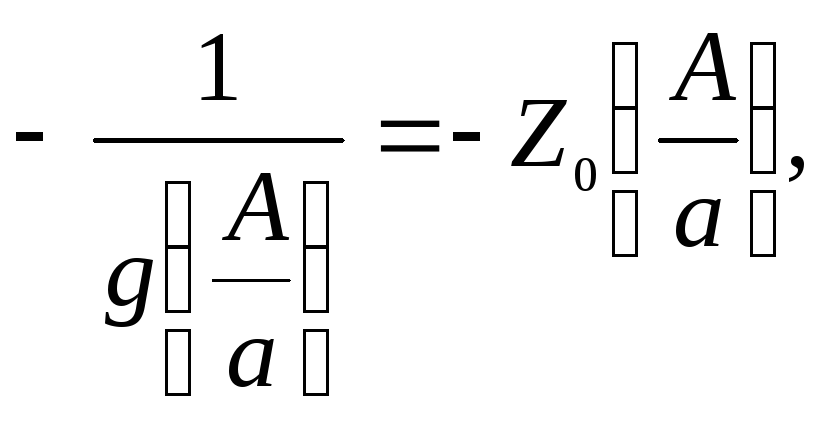построенная на основании рис. 2.7,б, располагается на вещественной оси, что справедливо для однозначных нелинейностей.

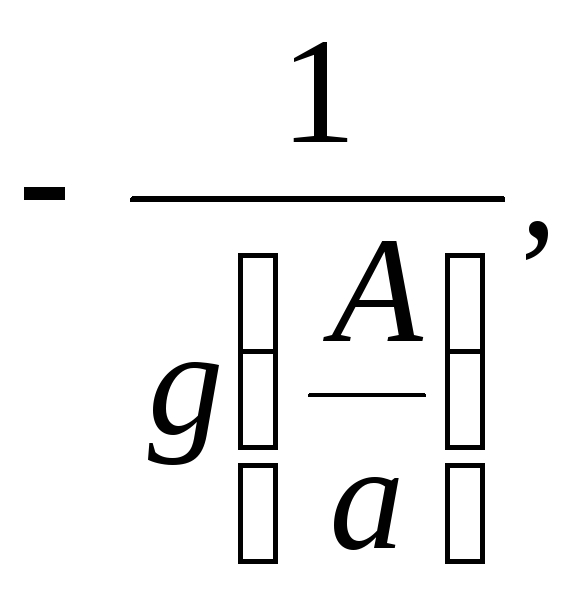Поскольку существует пересечение характеристик в точкеS, то необходимо с помощью критерия устойчивости колебаний в нелинейных САУ проверить возможность существования автоколебаний в этой точке. В соответствии с этим критерием колебания будут устойчивы, если точка амплитудной характеристики соответствующая увеличенной амплитуде А синусоиды на входе НЗ, не охватывается характеристикой. Следовательно, в точкеS существуют автоколебания, амплитуда которых А_а определяется по характеристике а частота _а – по АФХ .

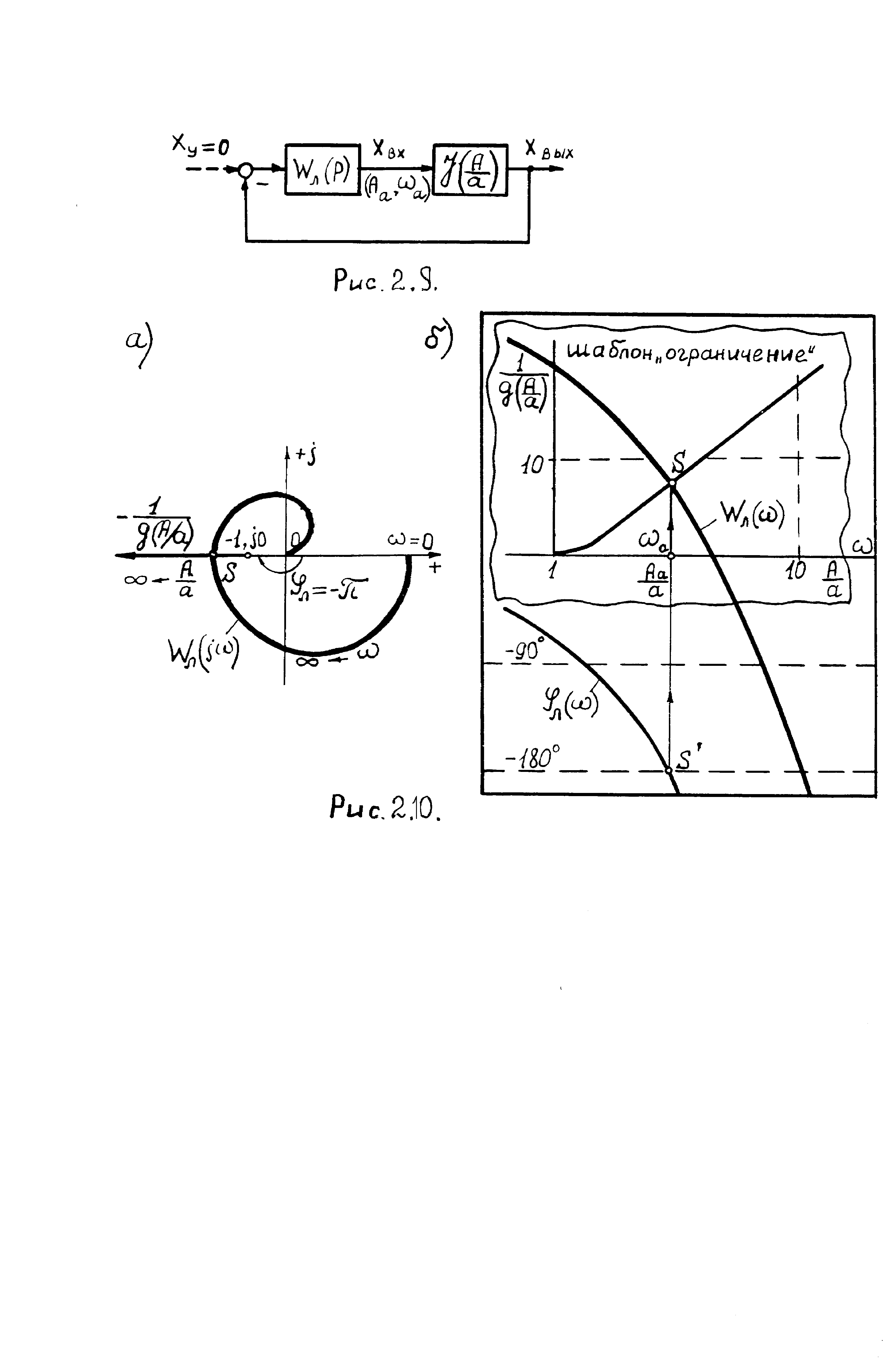
Рис. 2.9.

а б

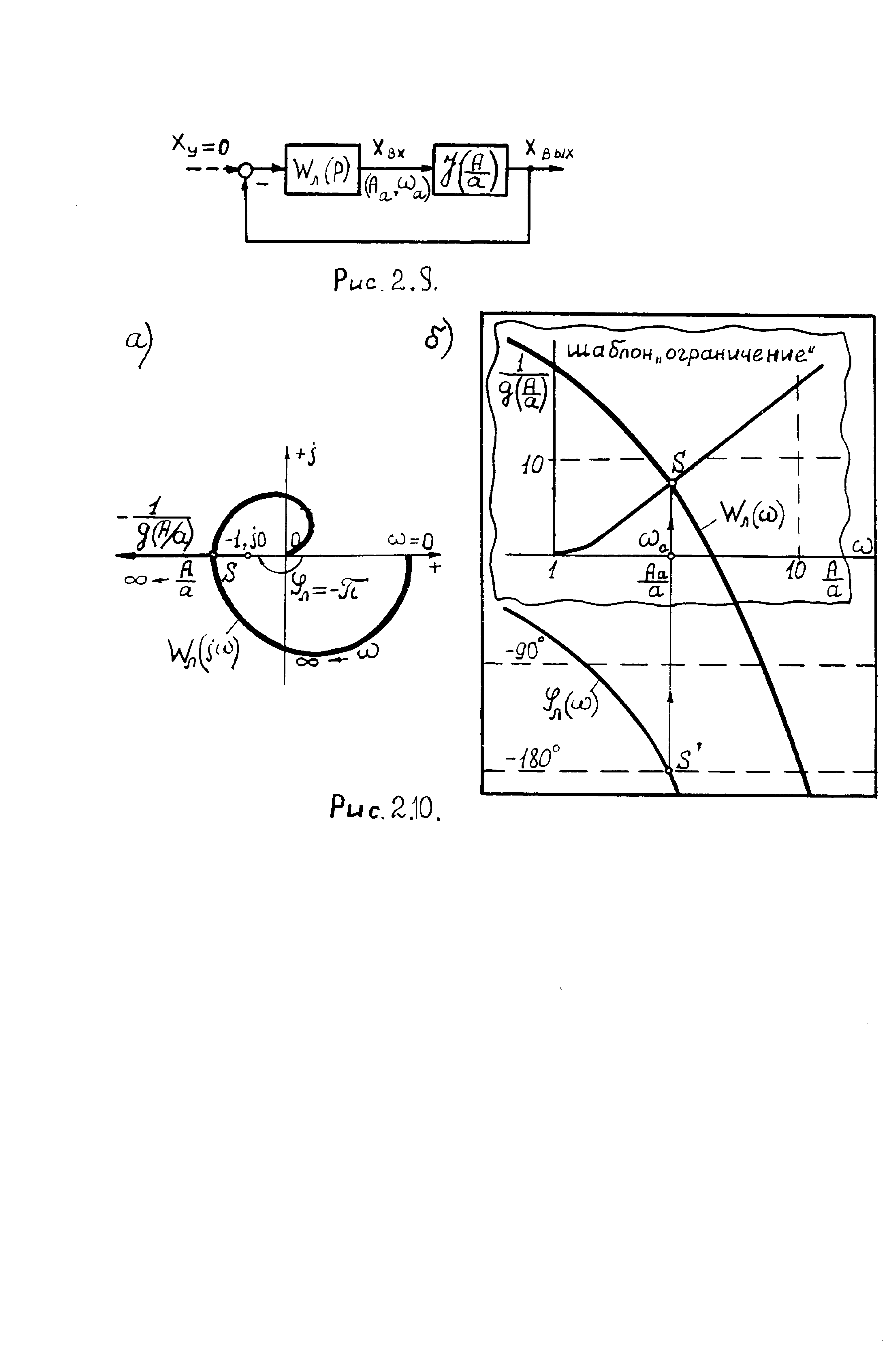
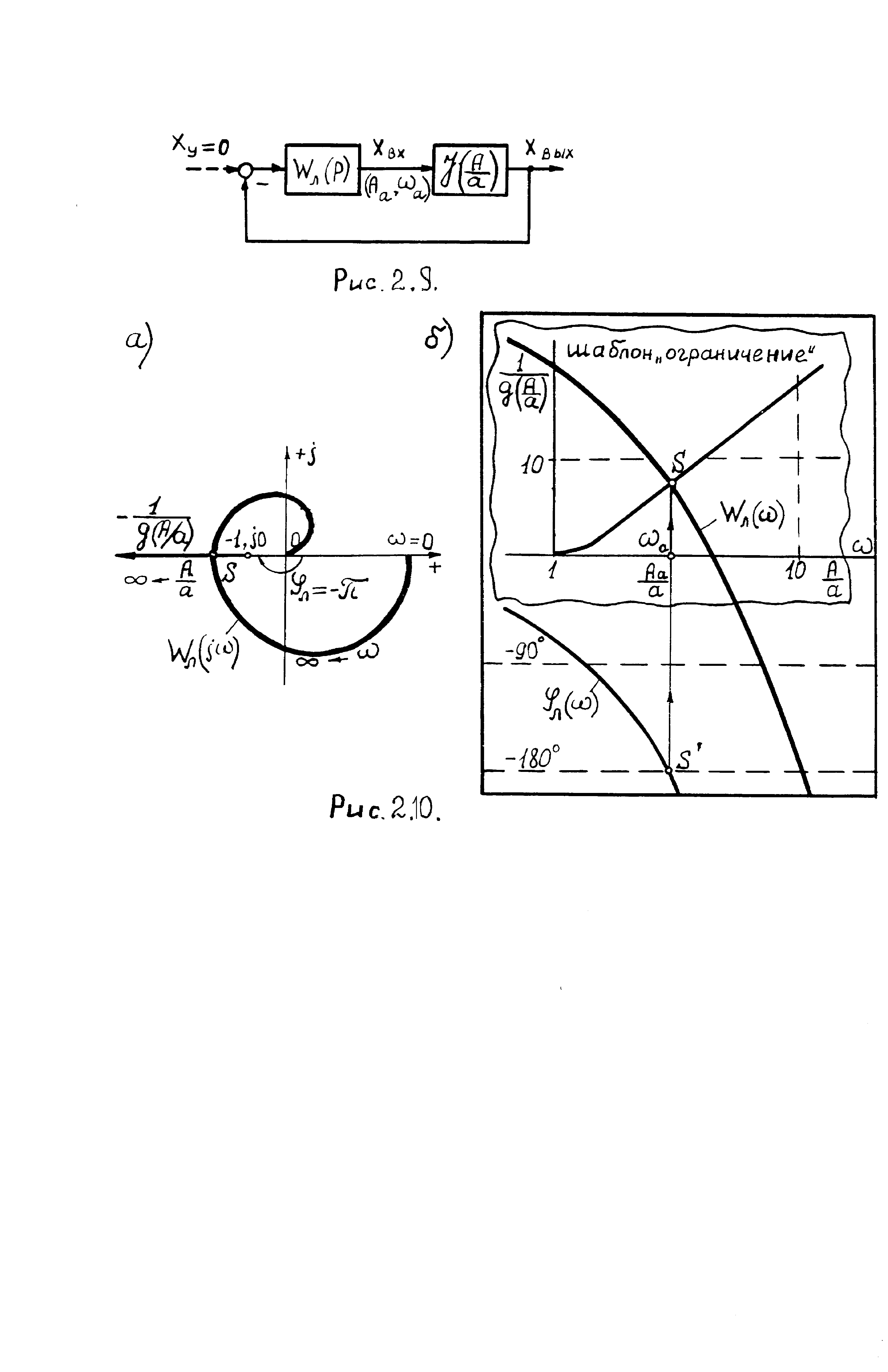
Рис. 2.10.

Аналогичное исследование более удобно провести с помощью метода логарифмических характеристик, что облегчает сам процесс построения и дальнейшей коррекции нелинейной САУ за счет известных преимуществ этих характеристик. Уравнение гармонического баланса для однозначных нелинейностей

(2.19) в логарифмической форме записи будет:

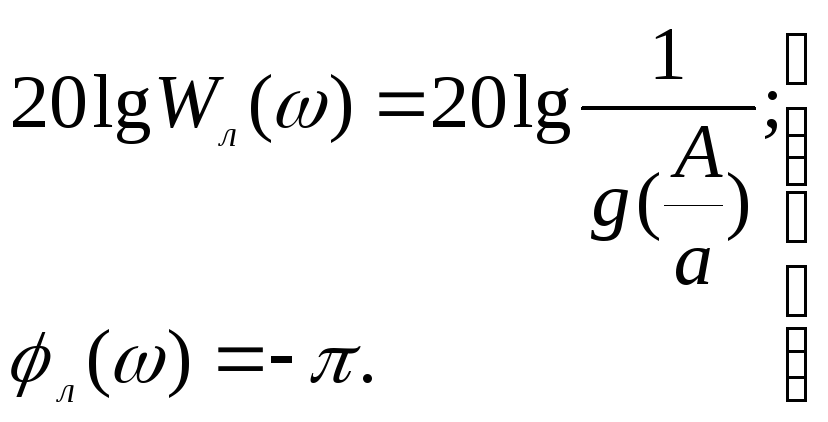(2.20)

Последнее равенство является следствием того, что условия гармонического баланса выполняются в точке S, лежащей на отрицательном участке вещественной оси, где фаза АФХ равна – 180⁰. Одновременность выполнения указанных условий применительно к логарифмическим характеристикам заключается в том, что точки пересечения ЛАХ W_л() и 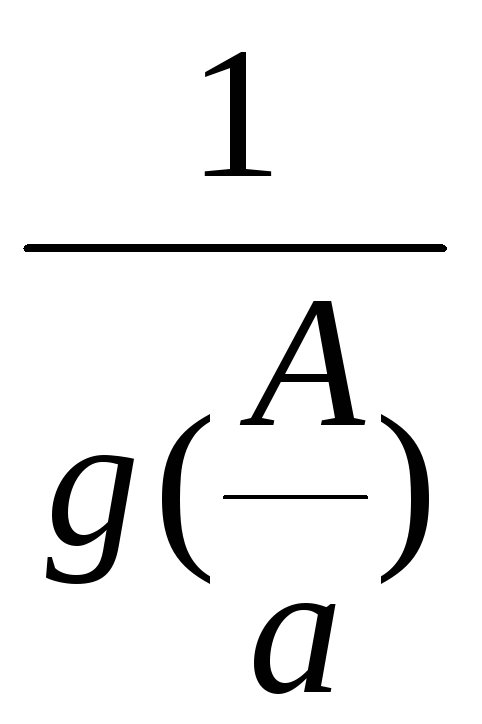и ЛФХ_л() и - должны лежать на одной вертикали. Соответствующие характеристики представлены на рис.2.10,б. При этом шаблон амплитудной характеристики НЗ типа «ограничение» (рис.2.7,в) наложен на ЛАХ W_л() таким образом, чтобы ось шаблона (А/а) совпадала с осью , а точка пересечения характеристик W_л() и 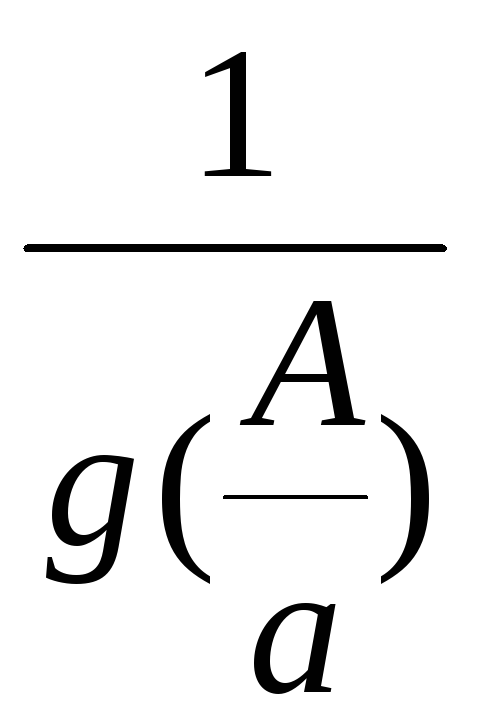находилась на вертикали пересечения ЛФХ_л() отметки –180⁰. Это положение шаблона является графическим решением уравнений гармонического баланса, и по шаблону определяется отношение А/а, т.е. амплитуда автоколебаний, а по ЛАХ W_л() – их частота _а.

Проведенное исследование показало, что в неустойчивой САУ, содержащей НЗ типа «ограничение», наблюдается автоколебательный режим работы. Для устранения автоколебаний необходимо скорректировать линейную часть системы, т.е. сделать ее устойчивой.

Метод гармонического баланса позволяет ответить на вопрос о существовании автоколебаний в нелинейной системе, однако он не дает возможности рассчитать переходные процессы. Построение переходных процессов в нелинейных системах частотными методами является предметом специальных разделов теории регулирования и изложено, в частности, в [1, 2, 11].

_________

Оглавление

Глава 1. Топологические преобразования динамических структурных моделей САУ....................................................................................................................3

1. Получение передаточных функций САУ путем структурных преобразований моделей систем....................................................................................................3

2. Использование теоремы Мейсона при получении передаточных функций САУ......................................................................................................................10

3. Структурно-матричные преобразования динамических моделей

САУ......................................................................................................................26