Задания Построить лчх (лах и лфх) системы по передаточной функции
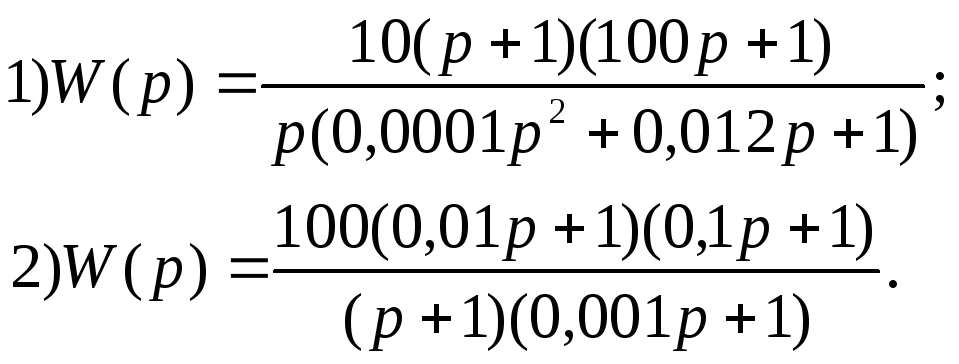
Вариант 1
Вариант 2
В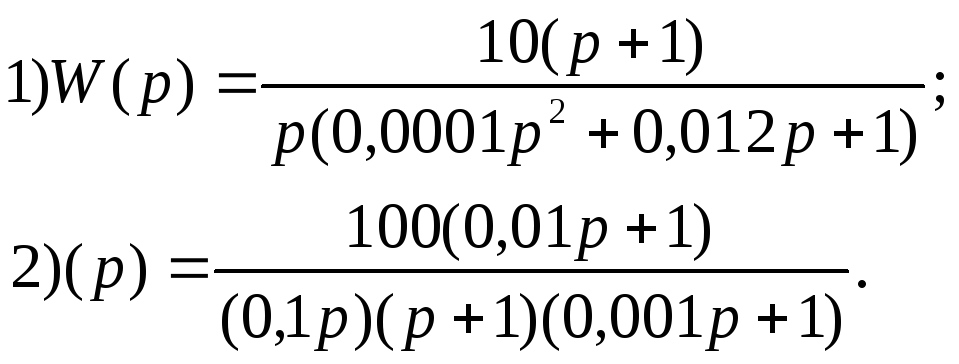
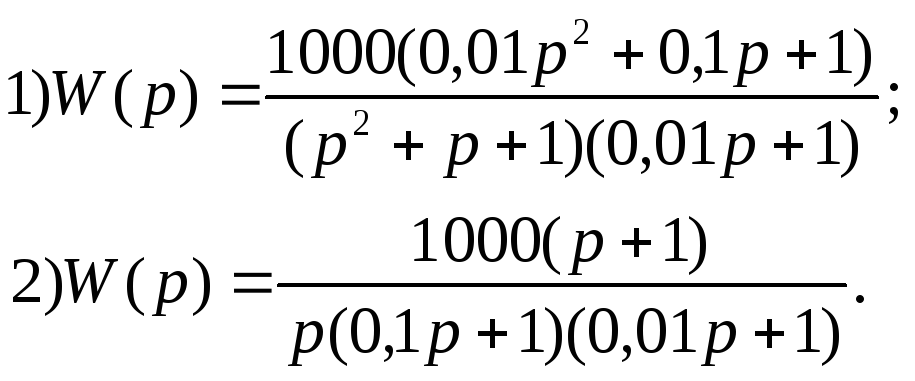ариант
3
В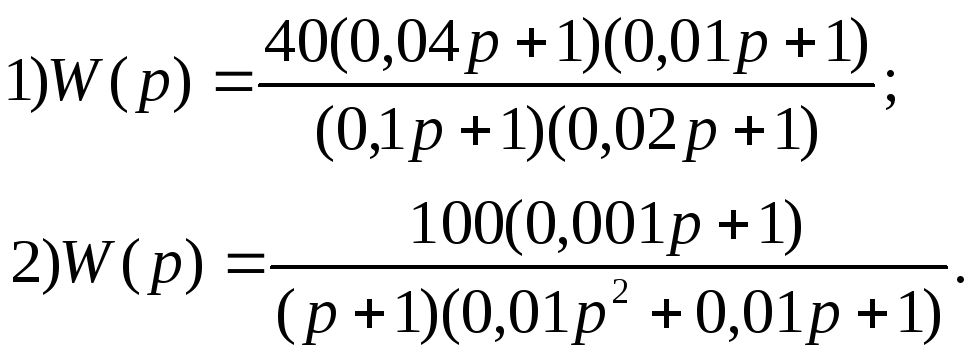
ариант
4
В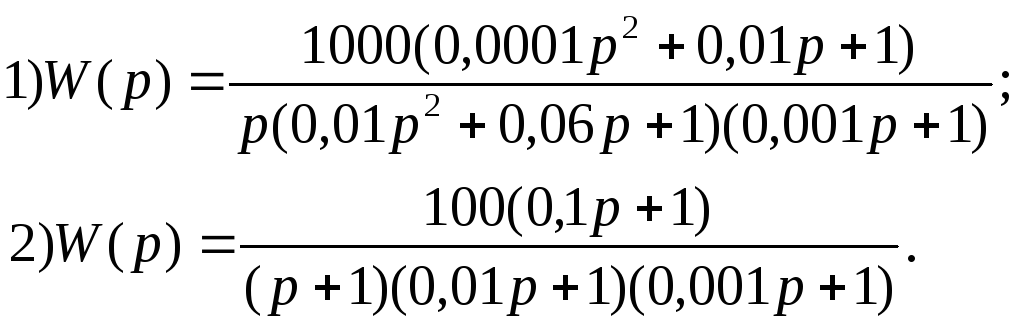
ариант
5
Вариант 6
В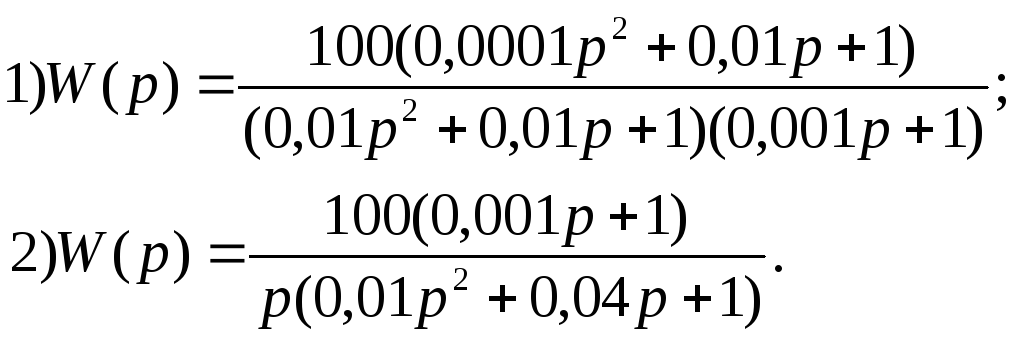
ариант
7
Вариант 8
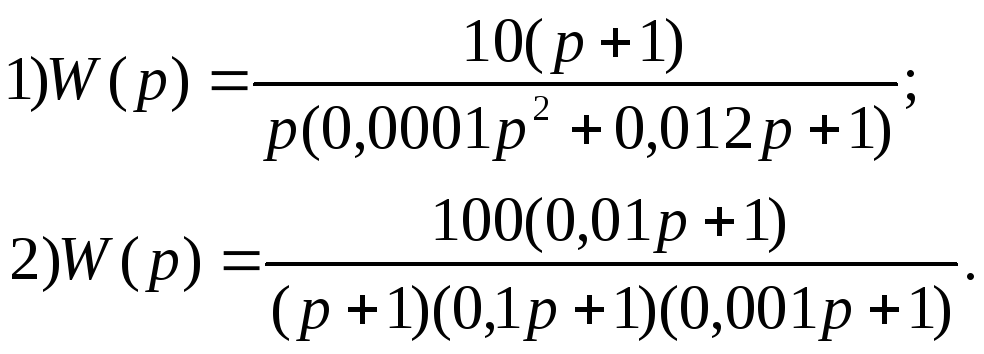
Вариант 9
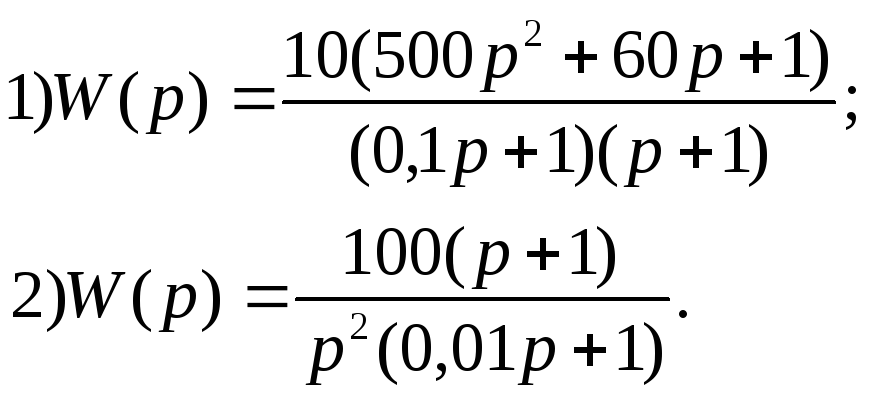
Вариант 10
В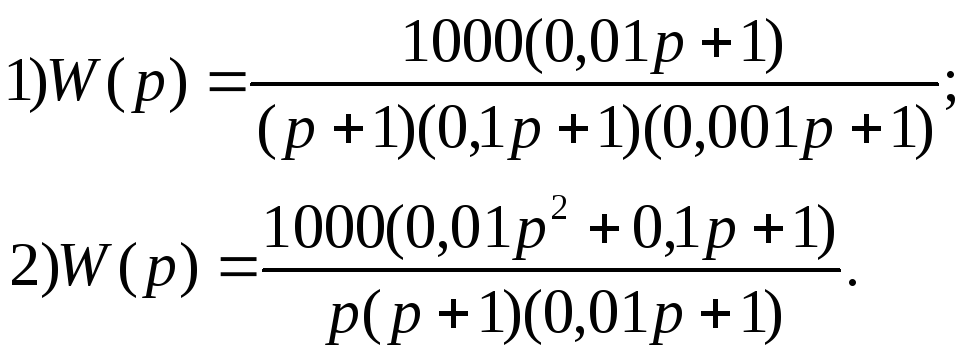
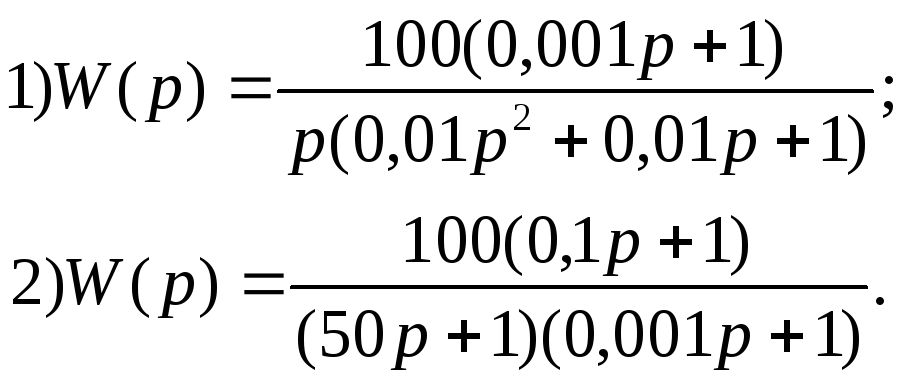ариант
11
Вариант 12
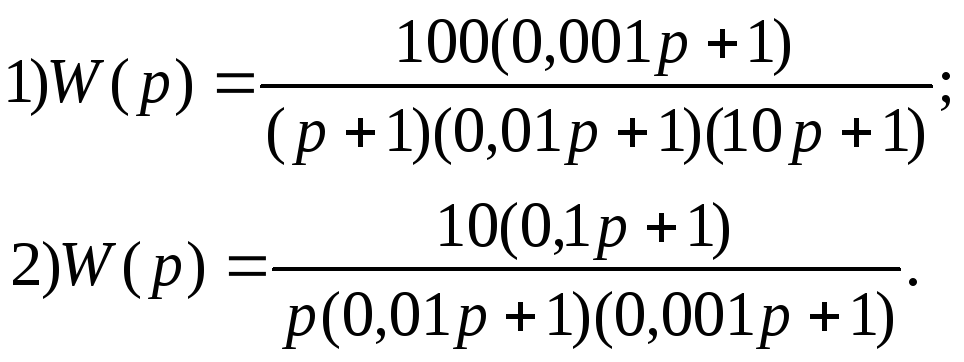
В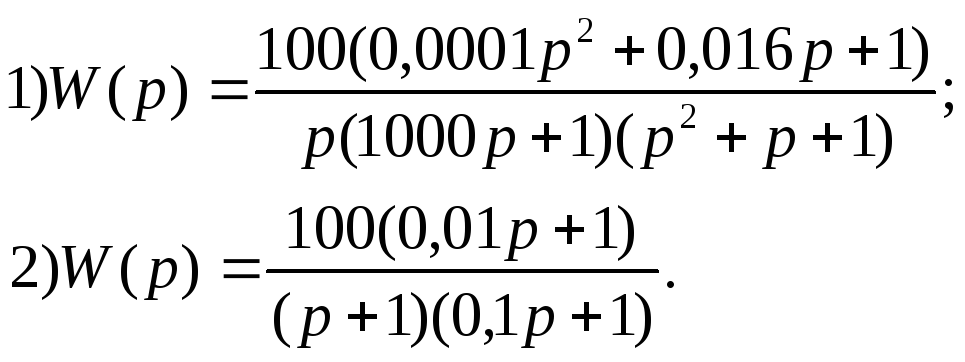
ариант
13
Вариант 14
В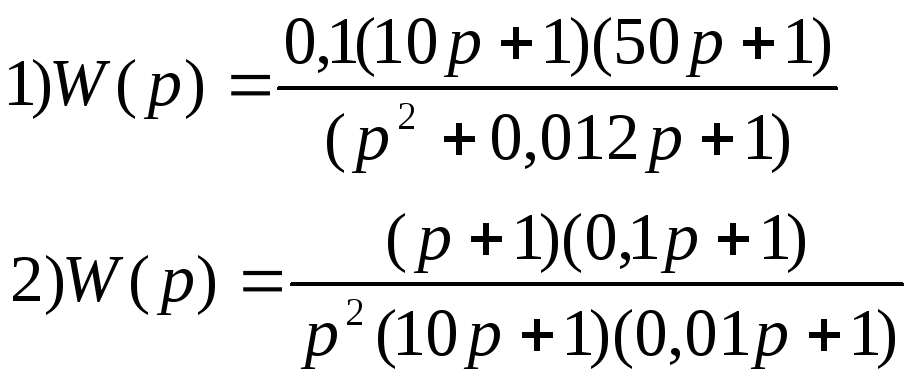
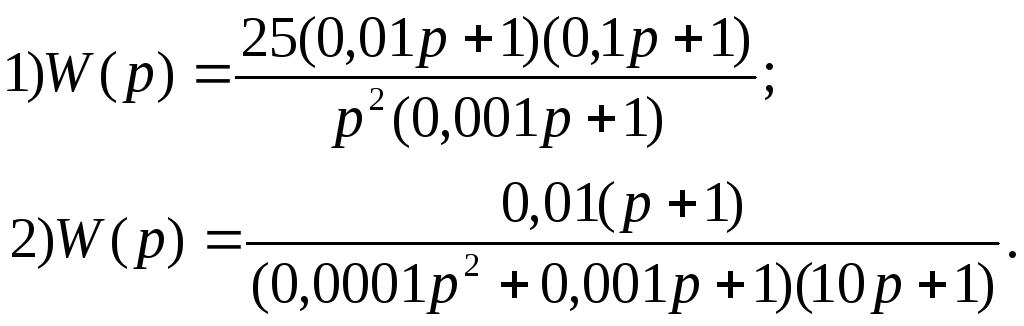ариант
15
Вариант 16
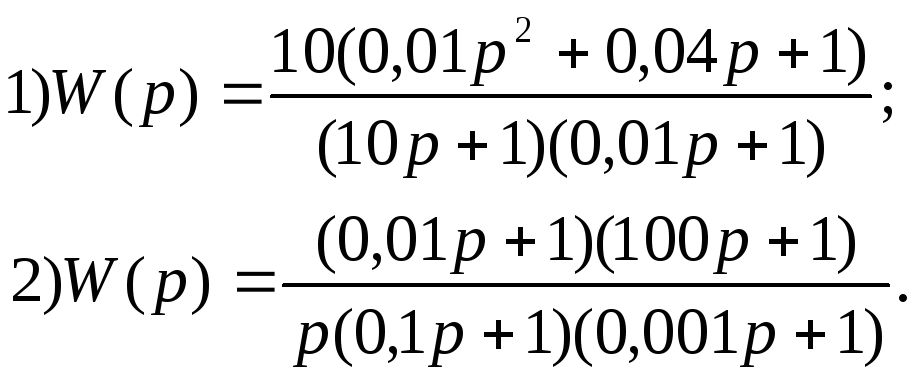
Вариант 17
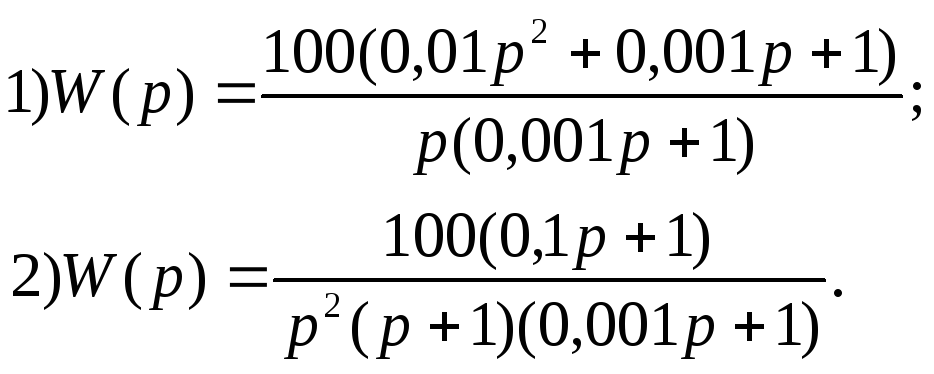
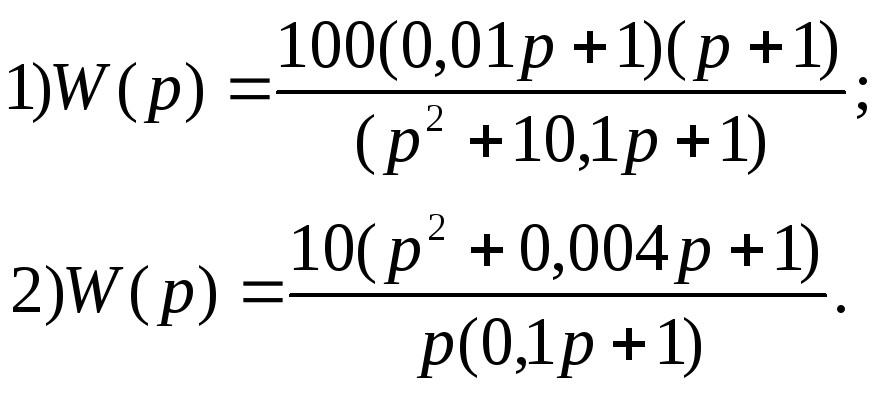
Вариант 18
Вариант 19
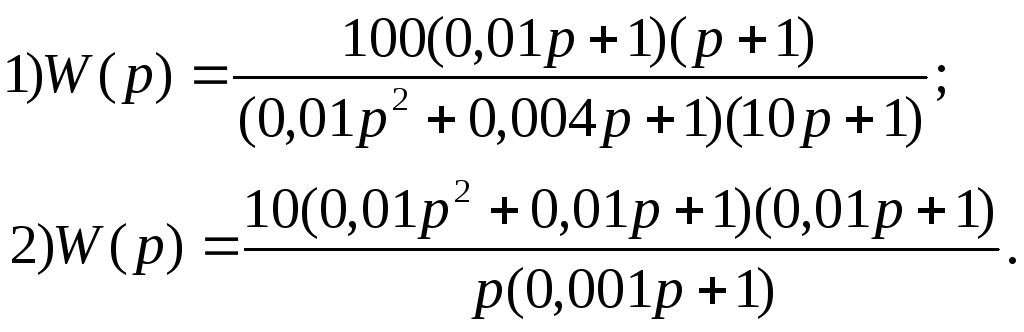
Вариант 20
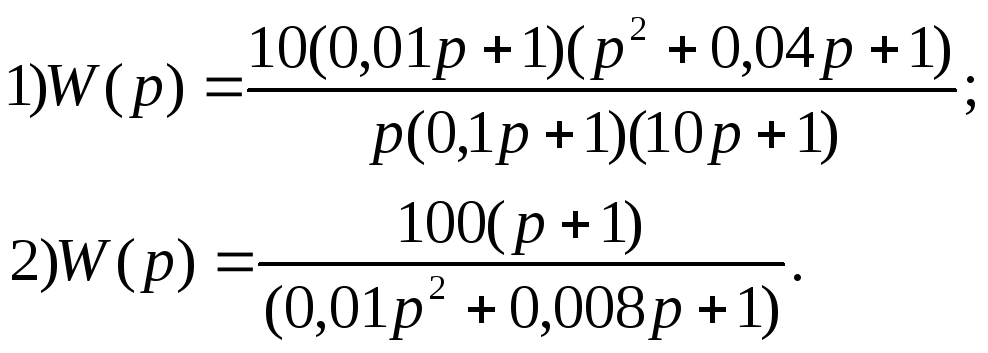
В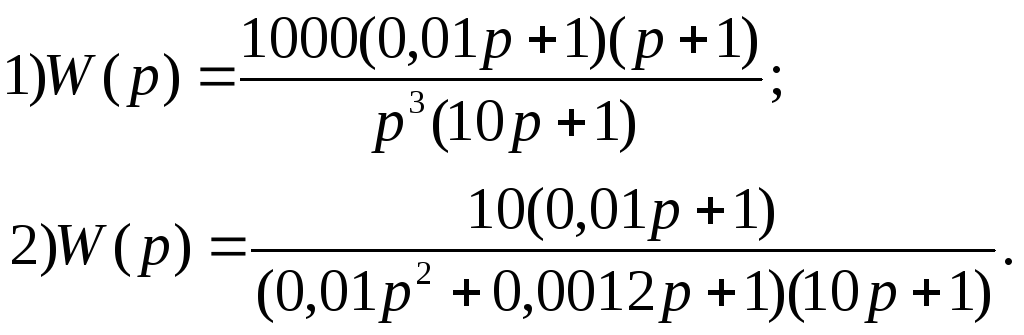
ариант
21
Вариант 22
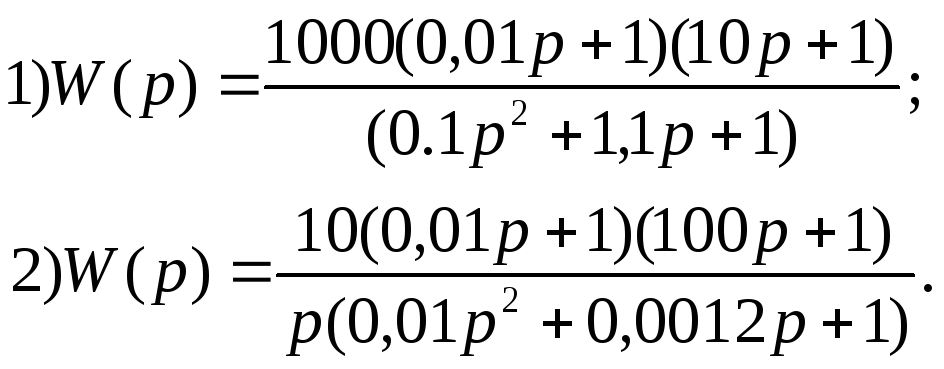
В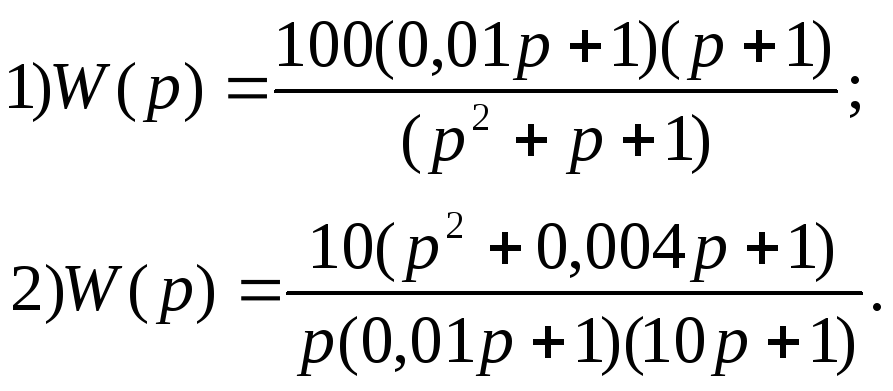
ариант
23
В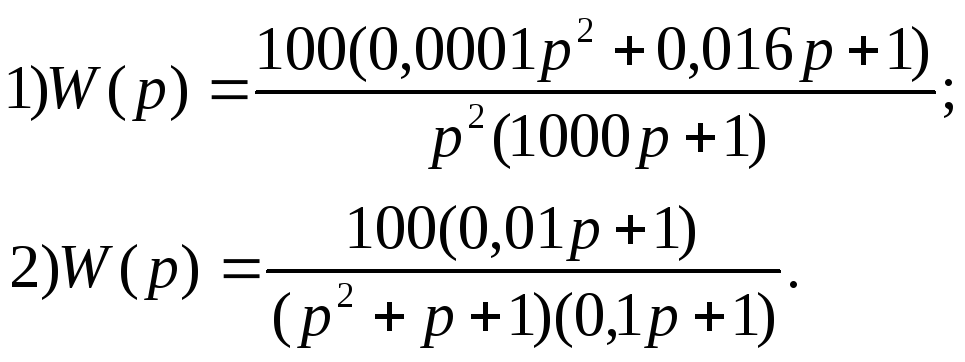
ариант
24
В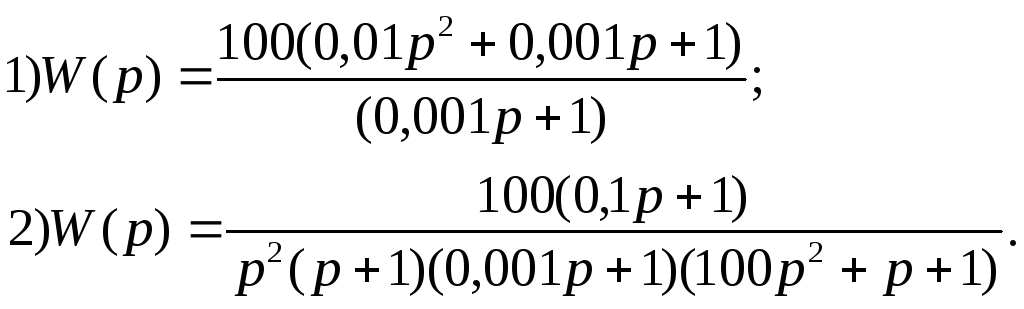
ариант
25
В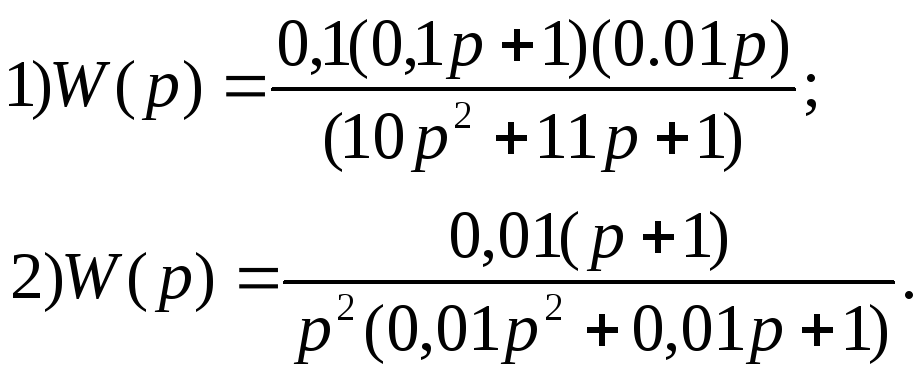
ариант
26
В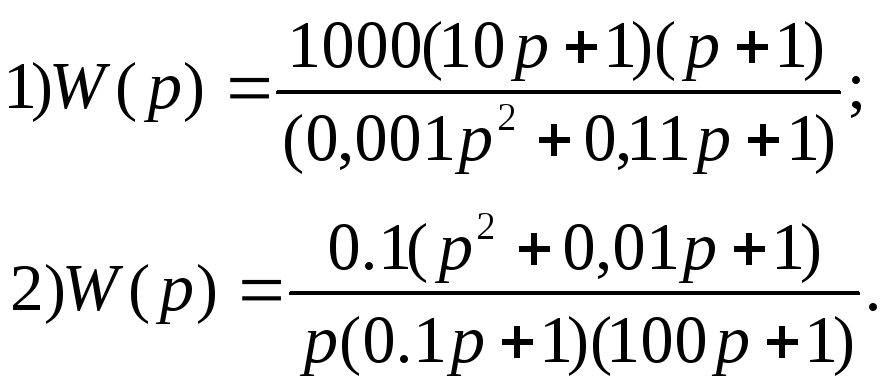
ариант
27
Вариант 28
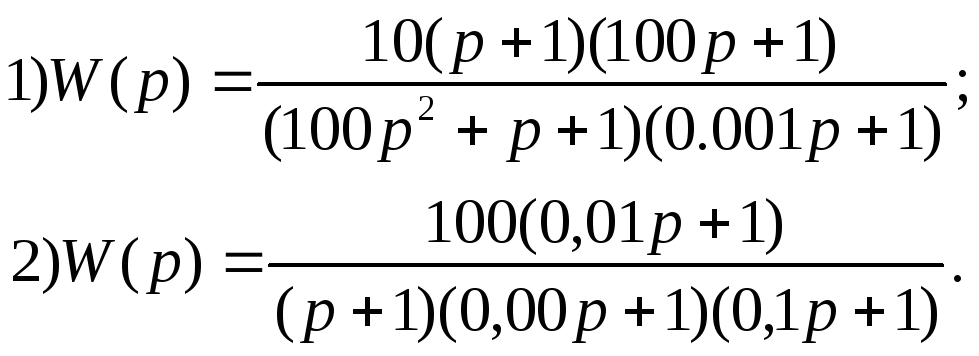
В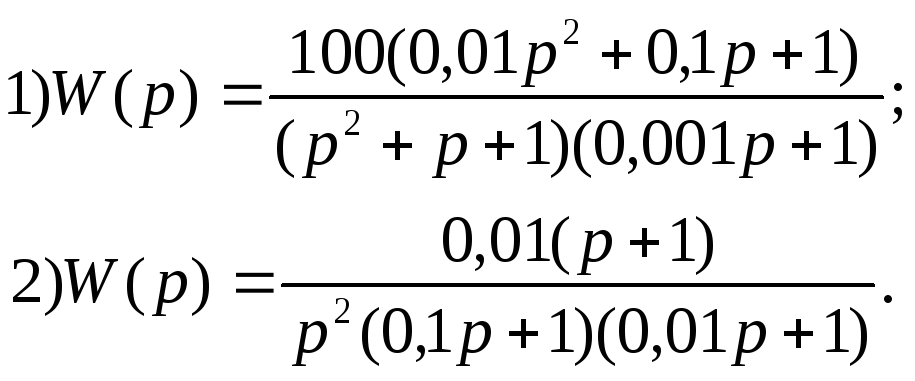
ариант
29
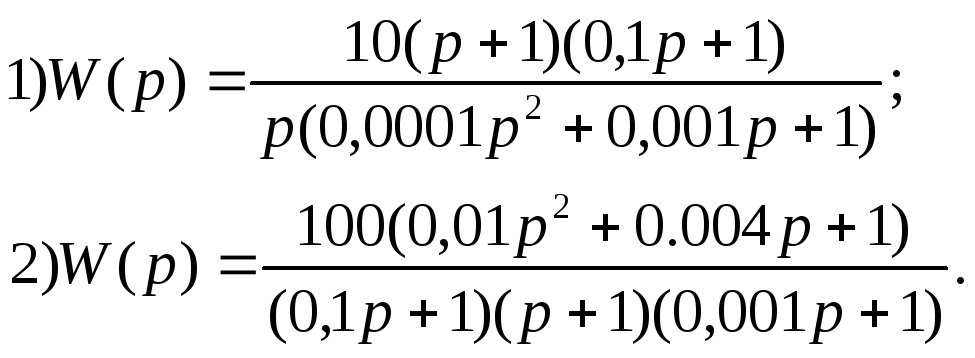
Вариант 30
2.3. Построение логарифмических частотных характеристик замкнутых САУ
Для последовательного соединения звеньев САУ, результирующие ЛАХ и ЛФХ могут быть получены графическим сложением соответствующих частотных характеристик звеньев.
Для соединений типа согласно-параллельного (рис.2.6,а) или встречно-параллельного (рис.2.6,б) (замкнутая САУ) построение результирующих логарифмических частотных характеристик осуществляется несколько сложнее.
а б
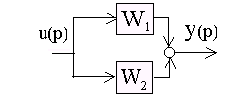
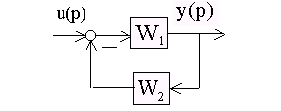
Рис.2.6
Если
звенья с частотными передаточными
функциями (ЧПФ)
и
соединены согласно-параллельно, то
результирующая ЧПФ
. (2.9)
Если в диапазоне частот << амплитуда А1()>А2(), обозначив А1=Аб,
A2=AM, 1=б, 2=М , перепишем (2.9) в виде
,
где Ap=AM/Aб 1; p=M-б .
Выражение (1+Аpejp) представляет собой частотную передаточную функцию эквивалентного последовательного звена
WП(j)=AПejп()=1+Ap ej p() .
Тогда выражения для ординат результирующих характеристик примут вид:
,
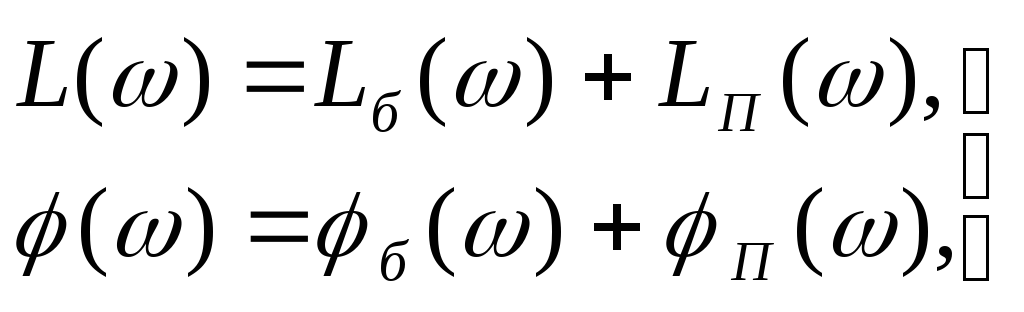(2.10)
где L()=20lgA(); Lб()=20lgAб(); LП()=20lgAП().
Если в некотором диапазоне частот А2()>A1(), то, обозначив А2()=Аб; 2()=б; А1()=АМ; 1()=М, получим для искомых ЛАХ и ЛФХ те же самые уравнения.
Из выражения (2.10) видно, что ординаты искомых частотных характеристик при согласно-параллельном соединении звеньев определяется ординатами характеристик звена с большей на данной частоте амплитудой Аб, сложенной с поправкой , определяемой по ординатам характеристик эквивалентного последовательного звена.
Для замкнутой САУ (рис.2.6,б) ЧПФ имеет вид:
,
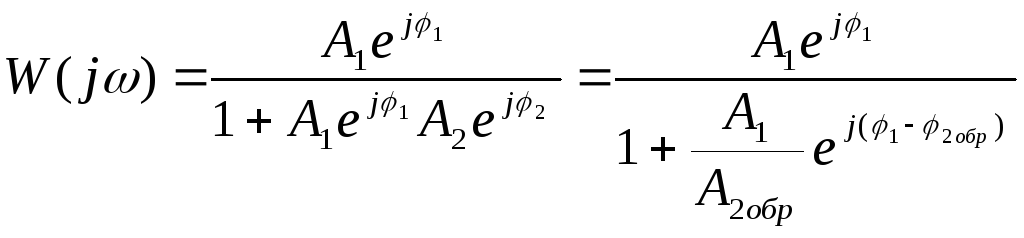где А2обр=1/А2; 2обр= - 2 – обратные значения амплитудной и фазовой характеристик звена в обратной связи.
Тогда в диапазоне частот, где А1<А2обр осуществляется замена А1=АМ; 1=М; А2обр=Аб; 2обр=б, и для результирующей ЧПФ получим:
,
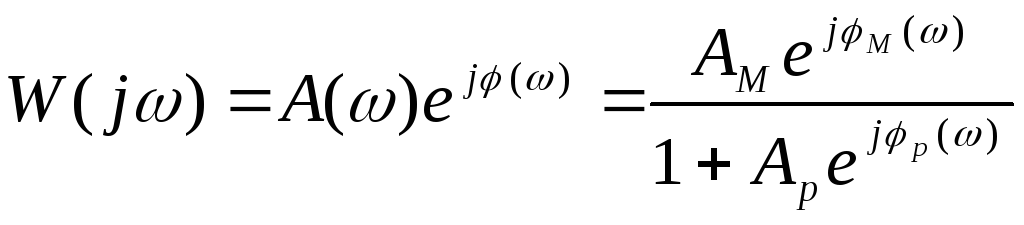где Аp=AM/Aб 1; р=М-б. Введём ЧПФ поправочного эквивалентного звена
и запишем выражения для результирующих ЛАХ и ЛФХ:
,
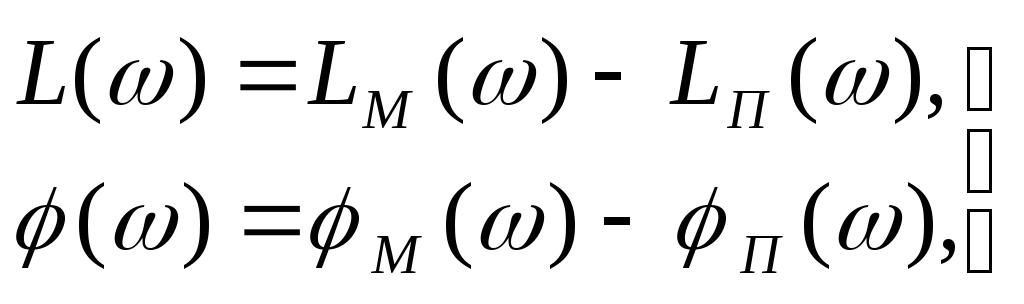(2.11)
где L()=20lgA(); LM()=20lgAM(); LП()=20lgAП().
В диапазоне частот, где А1>А2обр, осуществляется замена A1=Aб; 1=б; А2обр=АМ;2обр=М, которая также приводит к форме (2.11) для нахождения искомых характеристик.
Таким образом, ординаты искомых частотных характеристик при встречно-параллельном соединении звеньев определяются в большей мере ординатами характеристик звена с меньшей на данной частоте амплитудой Аi за вычетом поправок, вычисляемых по значению ординат характеристик исходных звеньев.
Подчеркнём, что для звена, стоящего в обратной связи, необходимо изображать обратные ЛЧХ, которые могут быть получены из исходных L2() и 2() симметричным отражением относительно частотной оси.
На практике используется простейший способ приближённого построения ЛЧХ параллельных соединений, основанный на аппроксимированных характеристиках. Данный подход правомерен для систем, в которых отсутствуют соединения, приводящие к возникновению резонансных всплесков ЛАХ или к появлению неминимально-фазовых эквивалентных звеньев.
Правила построения аппроксимированных ЛАХ параллельных соединений получаются из сформулированных выше правил (2.10) и (2.11) построения точных ЛЧХ таких соединений в предположении, что амплитудные поправки равны нулю.
Тогда правило для построения приближенных ЛЧХ может быть сформулировано следующим образом.
Результирующая ЛАХ параллельно соединённых звеньев проводится по верхним участкам ЛАХ составляющих звеньев при согласно-параллельном соединении и по нижним участкам ЛАХ при встречно-параллельном соединении, причём при изображении исходных ЛАХ при встречно-параллельном соединении для звена в обратной связи изображается обратная ЛАХ.
Пример 1
Построить ЛАХ для согласно-параллельного соединения интегрирующего звена и апериодического первого порядка, где k1=100; k2=1000, T=0,1c.
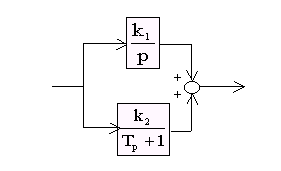
Решение. Изобразим ЛАХ указанных звеньев:
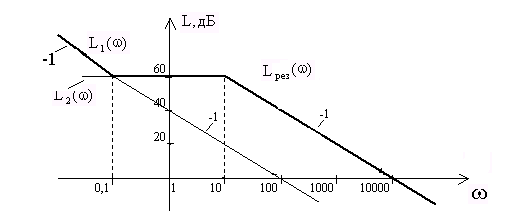
Обозначим ЛАХ интегрирующего звена L1(), а ЛАХ апериодического звена L2(). Очевидно, что в диапазоне частот 0<<0.1с выше расположена L1(), а при >0,1с-1 выше ЛАХ апериодического звена. Следовательно, результирующая ЛАХ Lрез() при <0,1с-1 проходит по L1(), а при 0,1с-1 – по ломаной L2().
Пример 2.
Построить ЛЧХ для встречно-параллельного соединения звеньев:
,
;
k1=1000; k2=0,01
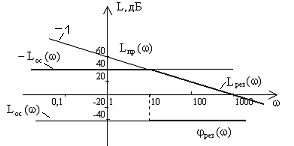
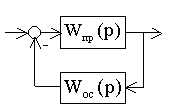
Изобразим ЛАХ интегратора, стоящего в прямой связи (Lпр()) и отрицательную ЛАХ звена в обратной связи: (-Lос()), представляющую собой прямую, параллельную частотной оси, проходящую на уровне +40дБ. Проводя результирующую ЛАХ Lрез()по нижним участкам, имеем ЛАХ Lрез()=Lос() при =10с-1 и Lрез()=Lпр() при 10с-1.