1. Рассмотрим пример

Перед тем как построить ЛЧХ данной системы, необходимо определить коэффициент демпфирования звена второго порядка, которое находится в числителе передаточной функции. Если этот коэффициент меньше единицы, то данное звено оставляем без изменения, если больше – то разбиваем на два звена первого порядка. Рассмотрим тождество:

где - коэффициент демпфирования. Из этого тождества следует:

откуда получаем Т₁=0,01с; =0,1. Следовательно, звено второго порядка является колебательным и остается без изменения.

Д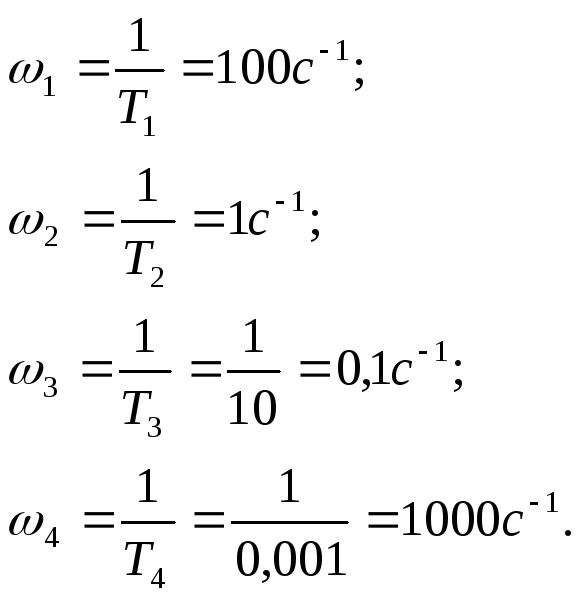алее, в соответствии с алгоритмом построения ЛЧХ, необходимо определить сопрягающие частоты:

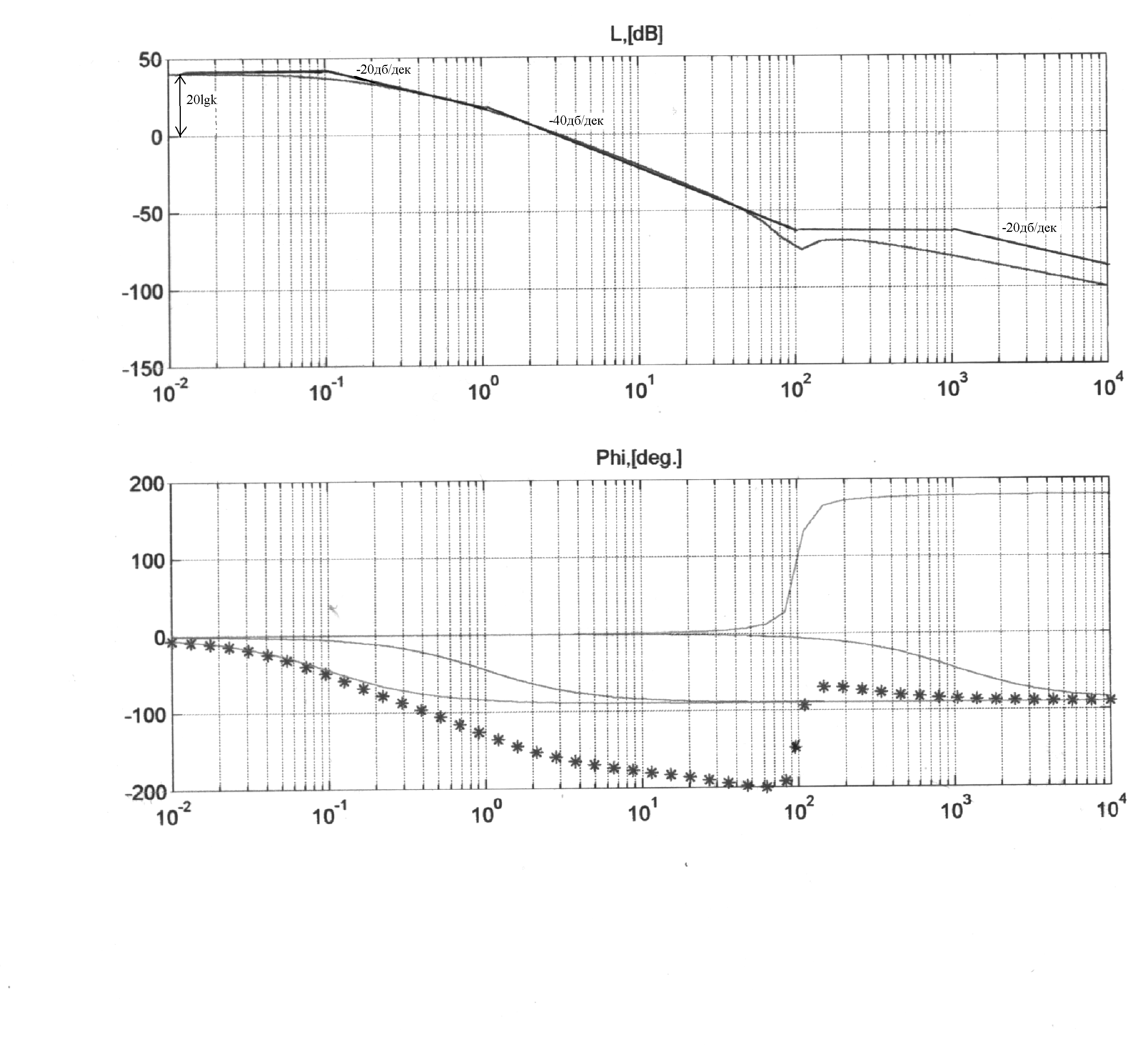
Нанесем данные частоты на логарифмическую ось абсцисс. В данной передаточной функции отсутствуют интегрирующие и дифференцирующие звенья. Следовательно, построение ЛАХ необходимо начать с горизонтального участка 20lgk (рис. 2.4,а). В рассматриваемом примере k=100. Тогда 20lg100=40дБ. Данная прямая находится в области низких частот слева от всех сопрягающих частот. На частоте ₃ прямая претерпевает излом на –20дБ/дек, так как эта частота относится к 1-му звену первого порядка (апериодическому звену), находящемуся в знаменателе передаточной функции. Прямую с этим наклоном проводим до частоты ₂. На этой частоте прямая снова претерпевает излом на –20дБ/дек. Суммарный наклон прямой теперь составляет –40дБ/дек. С этим наклоном ведем прямую до частоты ₁. Частота ₁ относится к звену второго порядка, расположенного в числителе передаточной функции (форсирующему звену второго порядка). Следовательно, результирующая ЛАХ на этой частоте претерпевает излом на +40дБ/дек и на отрезке частот от ₁ до ₄ пройдет горизонтально. На частоте ₄ снова изменит свой наклон на –20дБ/дек. На рис. 2.4,а показана пунктирной линией точная ЛАХ W_c() с учетом поправок на изломах асимптотической характеристики системы.

Для построения ЛФХ системы () строят фазовые характеристики каждого звена в отдельности, а затем их складывают геометрически (рис. 2.4,б).

а

W_C()

₃ ₂ ₁ ₄ 

б

₁

₂ ₄

₃

_c()

₃ ₂ ₁ ₄ 

Рис. 2.4.

2. Рассмотрим еще один пример.

Передаточная функция системы имеет вид:

.

Н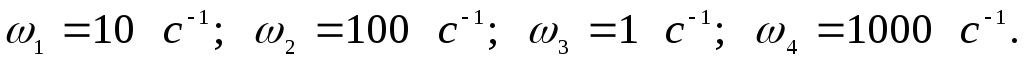айдем сопрягающие частоты:

Нанесем их на логарифмическую частотную ось (рис. 2.5,а). В данной передаточной функции присутствует интегрирующее звено, поэтому построение

а)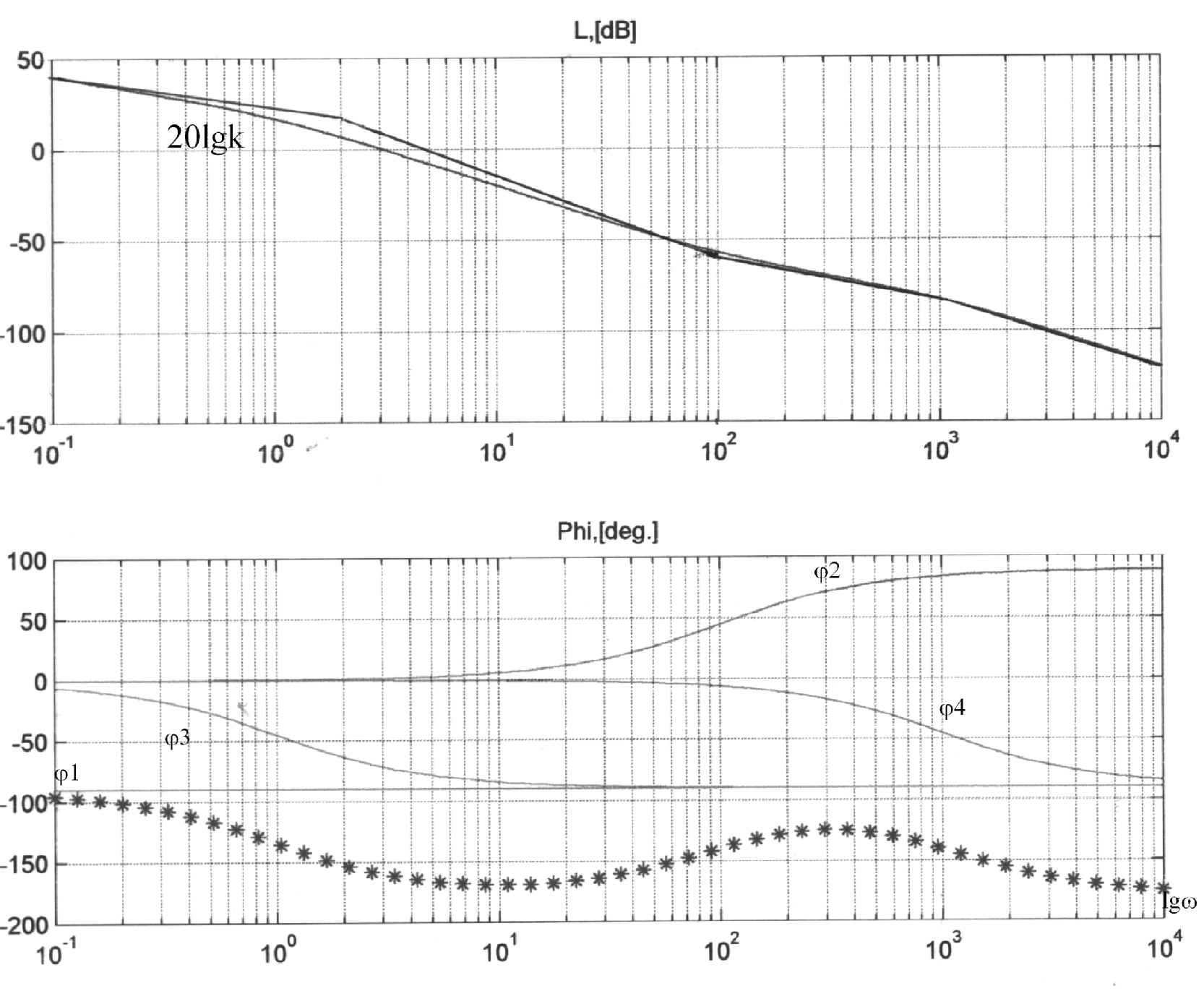

-20 дБ/дек

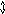
-40 дБ/дек

-20 дБ/дек

-40 дБ/дек

₁ ₂ ₃ 

б)

φ_с(ω)

₁ ₂ ₃

Рис. 2.5.

ЛАХ начинается с него. Для этого через частоту ₀=1с^-1 (lg=0) на уровне 20lgk=20дБ проводится прямая линия с наклоном -20дБ/дек. На частоте ₃ данная прямая претерпевает излом еще на –20дБ/дек, так как данная частота относится к апериодическому. До частоты ₂ прямая будет проходить с наклоном –40дБ/дек. На частоте ₂ прямая изменит наклон на +20дБ/дек, так как эта частота относится к звену первого порядка, расположенного в числителе (форсирующему звену). Данный наклон сохранится до частоты ₄. На частоте ₄ результирующая ЛАХ W_c() снова претерпит излом на –20дБ/дек и далее будет иметь наклон –40дБ/дек.

Построение результирующей ЛФХ представлено на рис. 2.5,б. Как и в предыдущем случае, сначала строятся фазовые характеристики каждого звена в отдельности, а затем результирующая характеристика получается путем их геометрического сложения. В данном случае результирующая ЛФХ _с() начинается не от нуля, а от -/2 за счет интегрирующего звена.