Глава 2. Частотный метод исследования динамики сау

2.1. Применение метода логарифмических частотных характеристик к анализу и синтезу линейных САУ

Несмотря на широкое развитие и применение машинных методов исследования САУ, интерес к частотному методу не уменьшился, а даже возрос за последние годы. Это обусловлено как универсальностью частотного метода и удобством синтеза систем, так и методологией самого процесса исследования САУ. В основе различных структурно-топологических методов лежит единое математическое описание, в общем случае система нелинейных дифференциальных уравнений, трансформирующихся в дальнейшим применительно к конкретным методам. При этом последние оказываются взаимосвязанными и дополняющими друг друга на каждом этапе исследования.

Применение частотного метода целесообразно на начальном этапе расчета САУ, поскольку с его помощью наиболее удобно «почувствовать» специфику работы системы, выявить существенные параметры и связи, исследовать влияние «малых» параметров, провести синтез регуляторов и корректирующих обратных связей и дать предварительную оценку динамических свойств САУ. Такое исследование проводится обычно для линеаризованной системы.

В основе частотного метода лежит операторный метод, поскольку получение комплексной спектральной функции W(j), иными словами, амплитудно-фазовой характеристики (АФХ), сопряжено с формальной заменой оператора р на j.

При этом связь между различными частотными характеристиками и передаточной функцией W(р) может быть представлена в виде:

(2.1)

где W(), () – амплитудно-частотная (АЧХ) и фазо-частотная (ФЧХ) характеристики;

P(), Q() – вещественная частотная (ВЧХ) и мнимая частотная (МЧХ) характеристики.

АЧХ и ФЧХ получаются при построении АФХ в полярных координатах, а ВЧХ и МЧХ – в декартовых.

Физически АЧХ и ФЧХ представляют собой реакцию звена (или системы) на гармоническое воздействие на входе:

(2.2)

с постоянной амплитудой А_вх, начальной фазой _вх и переменной частотой .

При этом на выходе звена (системы) устанавливаются гармонические колебания:

(2.3)

с той же частотой, но с отличными в общем случае амплитудой и фазой. Тогда W()=А_вых()/А_вх() является АЧХ, а ()=_вых()-_вх() ФЧХ. Последние соотношения служат для экспериментального определения частотных характеристик с помощью специализированной аппаратурой [14].

На практике получили распространение логарифмические частотные характеристики (ЛЧХ) [1, 2, 3, 4], строящиеся в координатах lg(с^-1) по оси абсцисс и 20lgW() (дБ) по оси ординат. Преимуществами ЛЧХ перед обычными частотными характеристиками являются:

• возможность суммировать ЛЧХ последовательно соединенных звеньев САУ;

• удобное изображение на чертеже величин, несоизмеримых в натуральном масштабе, например, 0,01 и 100;

• аппроксимация характеристик звеньев САУ прямыми линиями;

• удобство синтеза САУ.

При определении в процессе синтеза САУ в общем виде коэффициента передачи объекта регулирования на различных частотах и параметров регуляторов можно руководствоваться построениями, выполненными на рис.2.1, и позволяющими определить изменение уровня ЛЧХ в заданном диапазоне частот в зависимости от степени наклона характеристики n (где n=1 соответствует наклону 20(дБ/дек), n=2 соответствует 40(дБ/дек) и т.д.). На рис. 2.1,а показано отрицательное изменение уровня ЛЧХ в дБ, на рис. 2.1,б – положительное. При определении же модуля изменения уровня ЛЧХ следует брать отношение большей постоянной времени или большей частоты к меньшей, т.е. 20lg(Т₁/Т₂)ⁿ или 20lg(₂/₁)ⁿ. Полезно помнить также, что высота резонансного всплеска ЛЧХ колебательных звеньев составляет 20lg(1/(2)), где  - коэффициент демпфирования звена.

При динамическом расчете САУ используются ЛЧХ как разомкнутой, так и замкнутой систем. Информацию о переходных процессах содержат как те, так и другие характеристики.

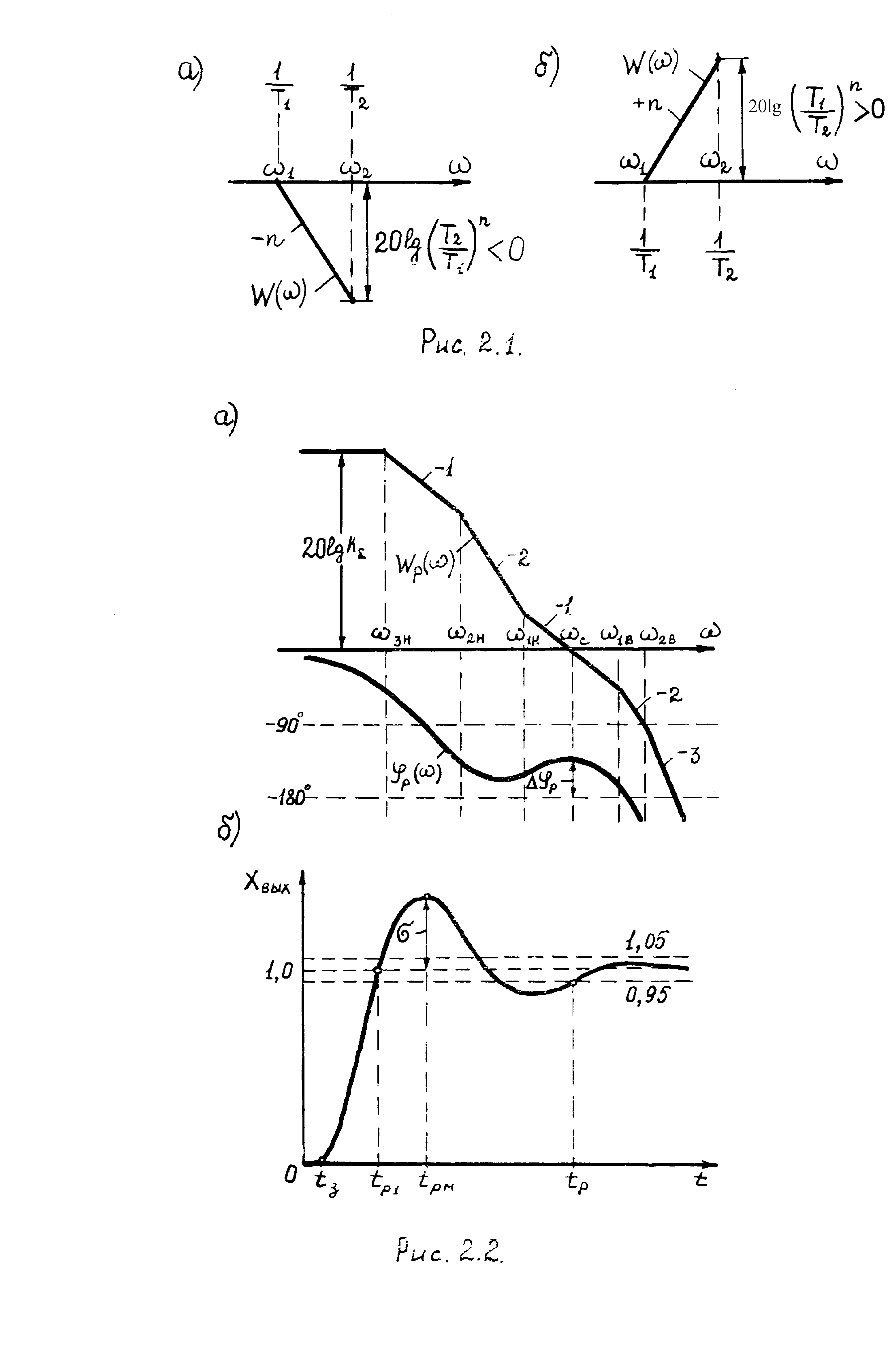
Рассмотрим сначала связь переходных процессов в замкнутой системе с ЛЧХ разомкнутой САУ. На рис.2.2,а показаны типовые логарифмические амплитудная (ЛАХ) и фазовая (ЛФХ) характеристики разомкнутой системы, на рис. 2.2,б – соответствующая переходная функция замкнутой САУ Х_вых(t) [реакция на единичный скачок Х_вх(t)=1]. Параметры переходного процесса и ЛАХ связаны между собой следующими формулами [15]:

1-sin_р; (2.4)

t_з(1/_1в)+(1/_2в); (2.5)

t_р1(1,5…2)/_с ; (2.6)

t_рм(3/_с); (2.7)

t_р3/_с +2/_1н . (2.8)

Из формул видно, что быстродействие системы прямопропорционально частоте среза _с , а колебательность обратно пропорциональна запасу по фазе _р. При _р0 отрицательная обратная связь становится положительной, что приводит к неустойчивости замкнутой САУ.

Хотя приведенные формулы являются приближенными (погрешность формул может составлять до 20…25%), их применение оказывается весьма полезным при оценки динамики системы в первом приближении.

Как известно, характер переходных процессов определяется зоной существенных частот системы, ограничивающейся по оси ординат 15дБ. Чем ближе к частоте среза _с располагается участок ЛАХ, тем большее влияние он оказывает на характер переходного процесса. Если правая часть ЛАХ при >_с формирует начало переходного процесса, то левая ее часть при <_с – конец процесса. В частности, участок ЛАХ W_р() с наклоном – 2 (-40дБ/дек) в зоне частот _1н…_2н обуславливает восстановление скорости электропривода при изменении момента сопротивления М_с.

Проанализируем теперь связь переходных процессов с ЛЧХ замкнутой системы. При качественной оценке переходного процесса по управлению или возмущению следует руководствоваться общим правилом, что начальная часть переходного процесса определяется высокочастотной частью соответствующей ЛАХ, а конец процесса – низкочастотной частью характеристики. На рис. 2.3 приведены примеры связи ЛАХ и переходных процессов в САУ, иллюстрирующие данное положение. Нетрудно видеть, что форма переходного процесса напоминает форму ЛАХ, повернутой относительно оси ординат на 180⁰.

При этом, если ЛАХ замкнутой системы во всем диапазоне существенных частот проходит монотонно и не имеет резонансных подъемов над уровнем 20lgk₀, то переходная функция системы также монотонна (см. рис. 2.3,а). Если же в ЛАХ имеется резонансный всплеск на какой-либо частоте, то переходная функция имеет

а б

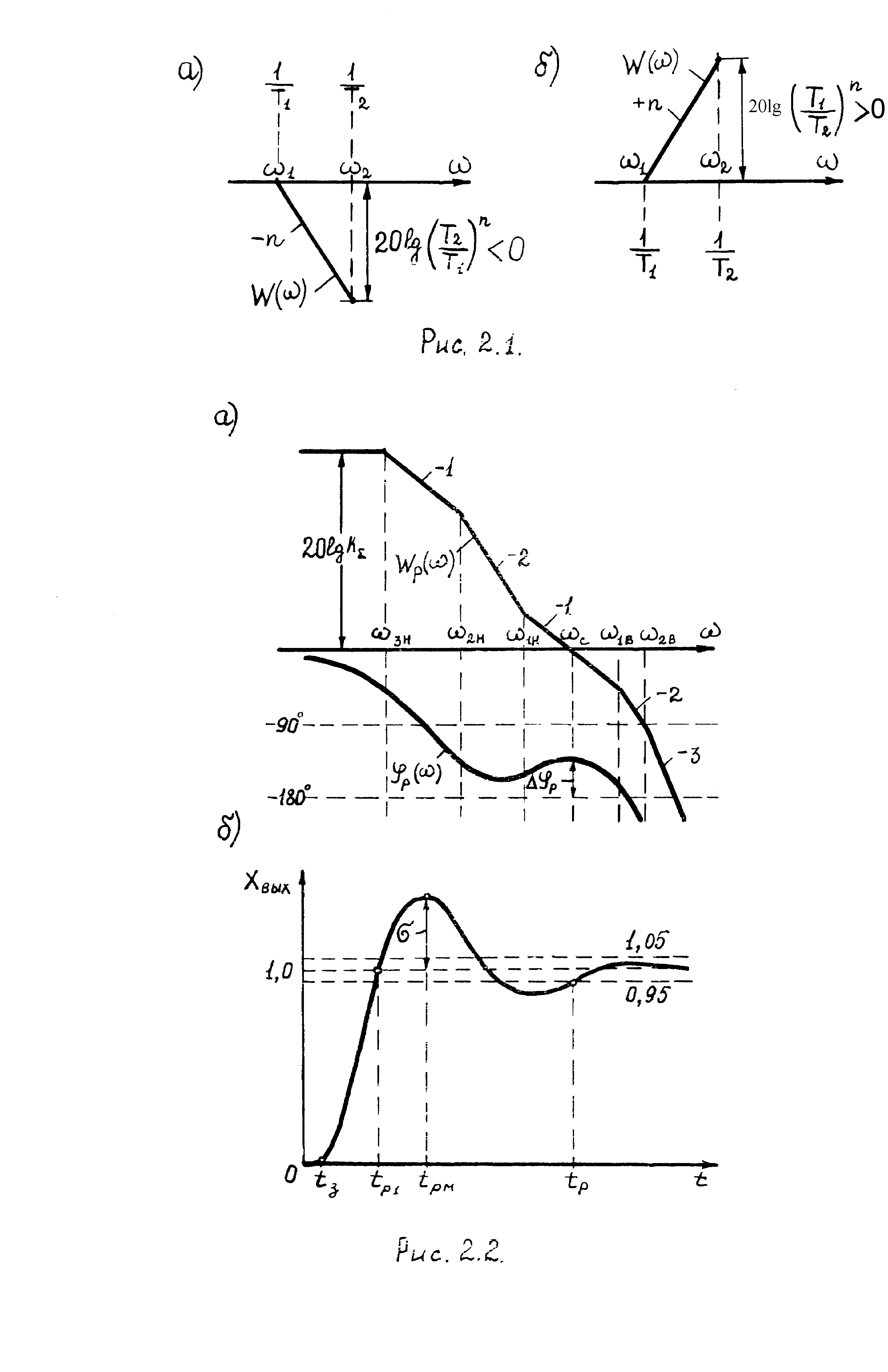
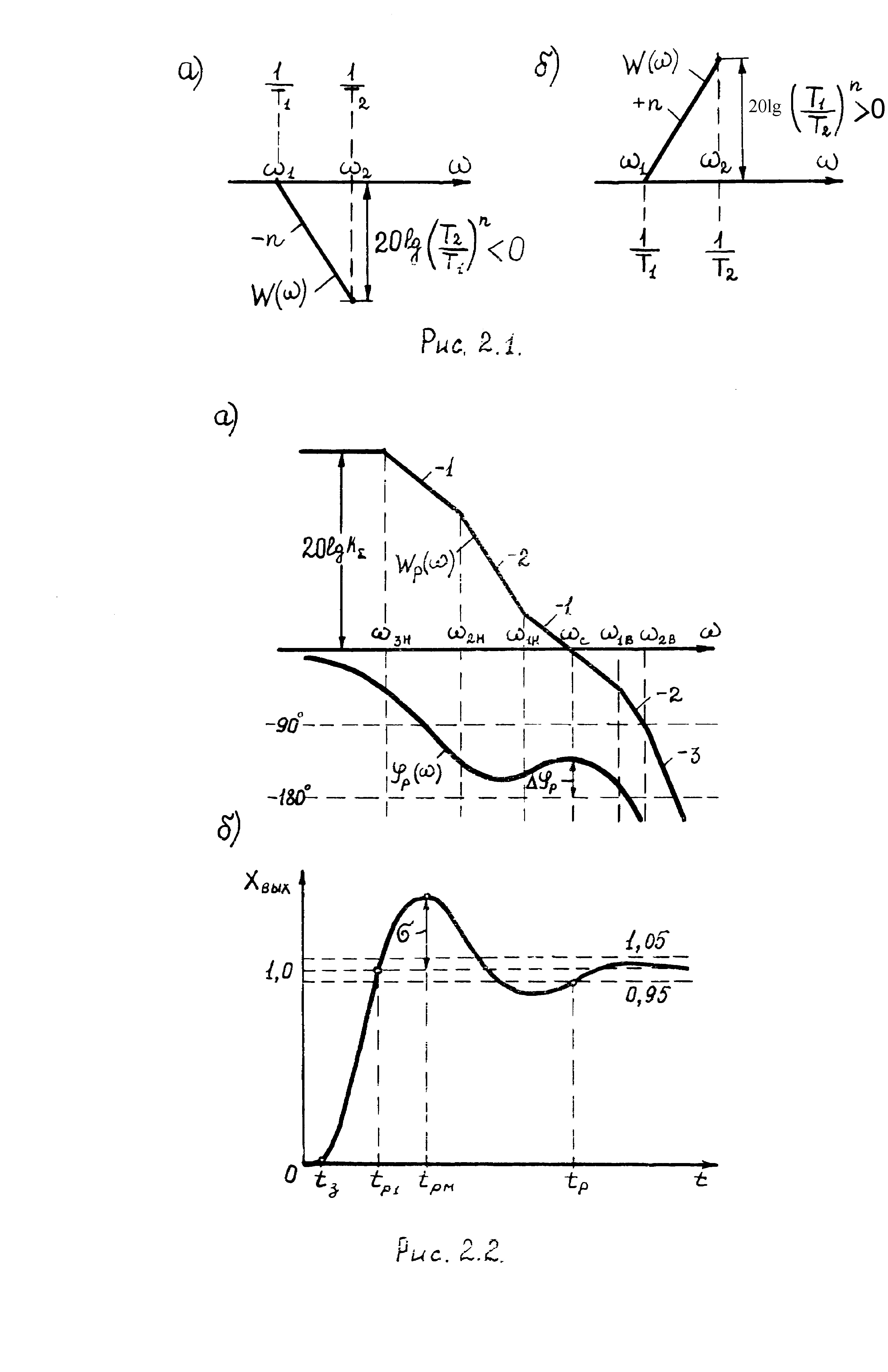
Рис 2.1.

а

б

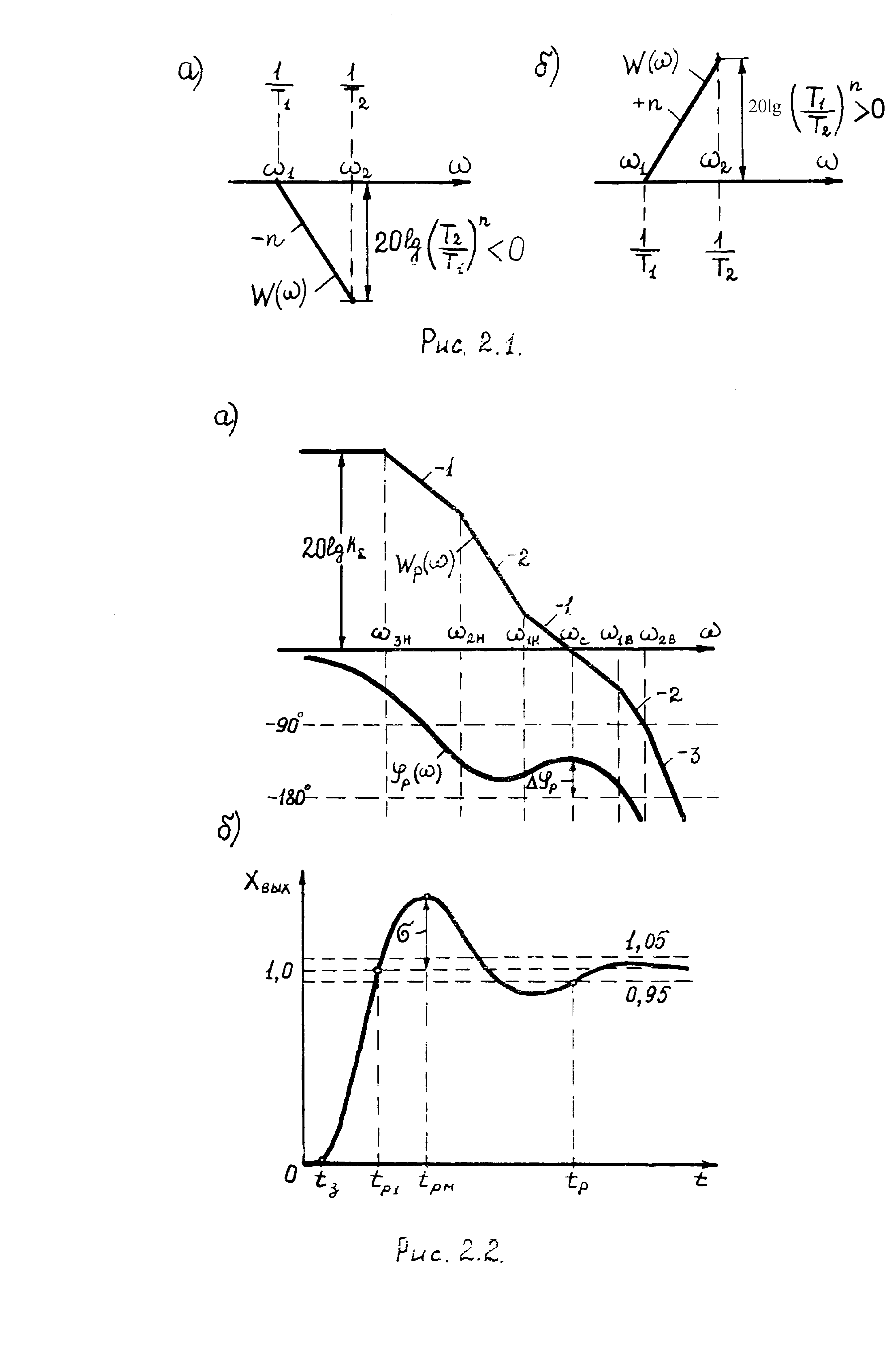
Рис. 2.2.

перерегулирование, определяемое коэффициентом усиления САУ на этой частоте (см. рис. 2.3,б).

а

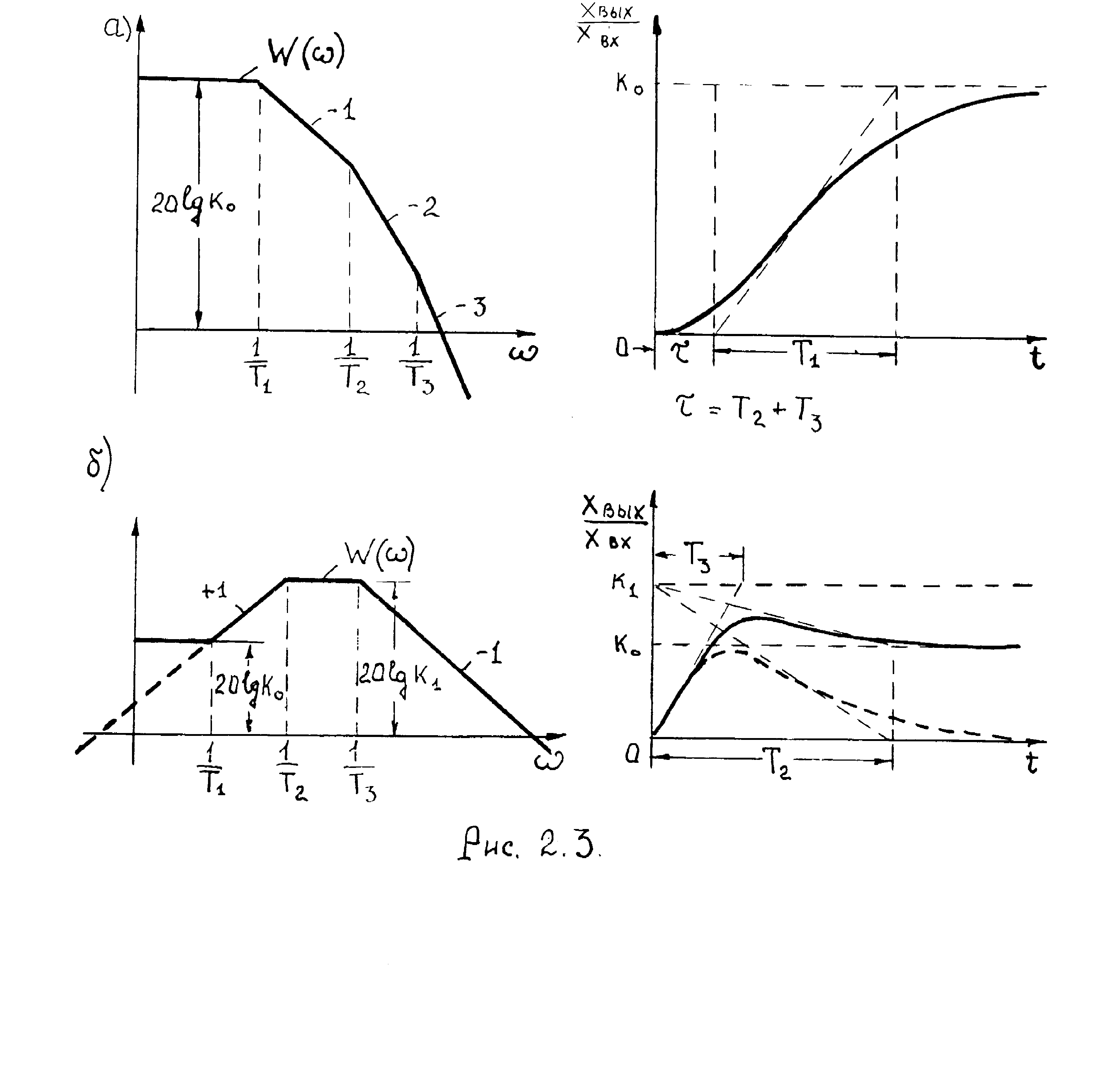
б

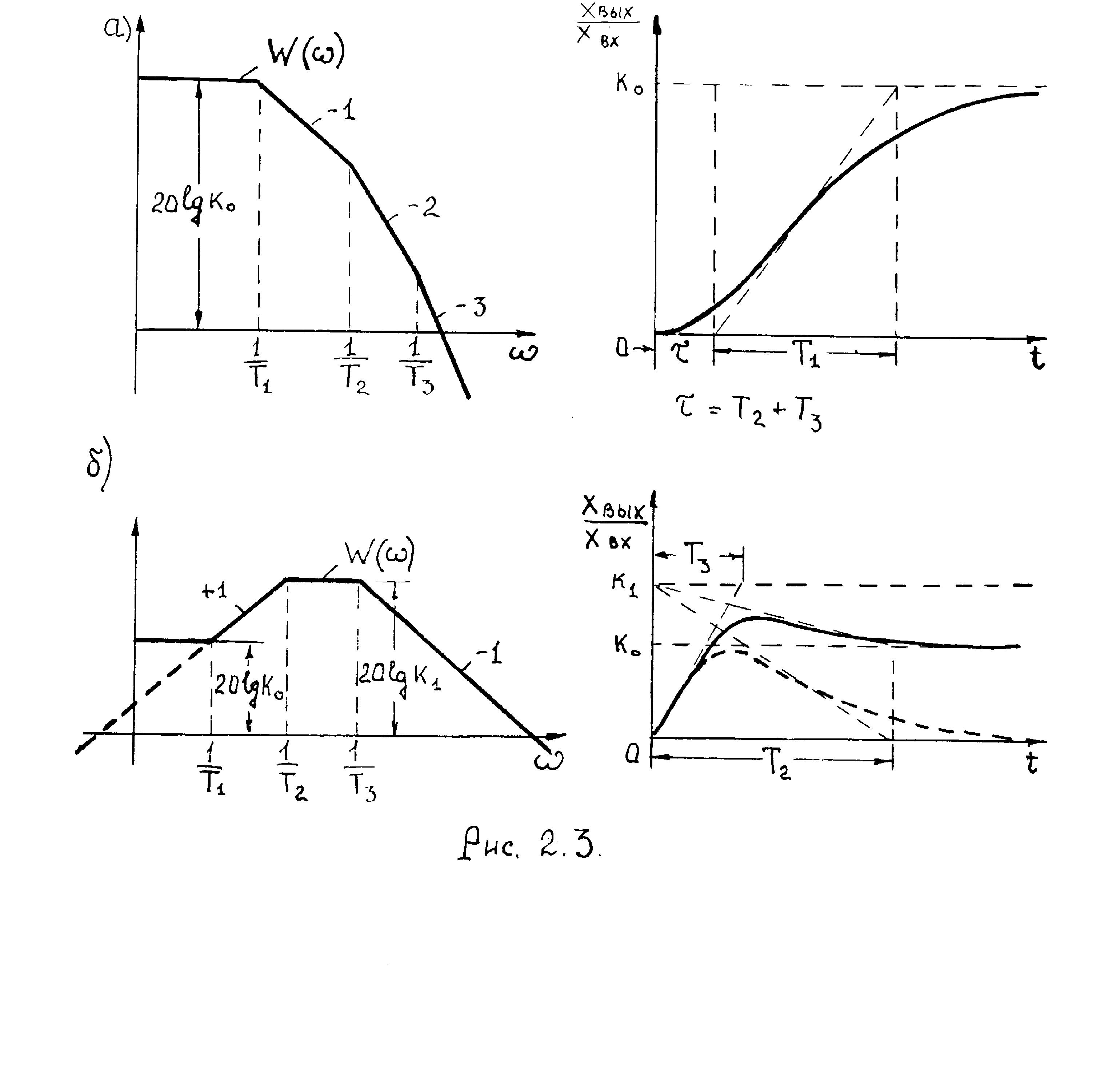
Рис.2.3.

Приведенные оценки переходных процессов в системе (или отдельном звене САУ) также являются приближенными, однако их использование помогает качественно оценить динамику САУ, не прибегая к расчету переходных процессов, или избежать возможных ошибок при выполнении подобных расчетов.

При исследовании динамики многоконтурных САУ нередкоприходится иметь дело с параллельно-встречным или с параллельно-согласным включением звеньев. Частотные характеристики таких соединений можно построить с помощью номограммы пересчета или специального приспособления – векторной линейки [6, 14]. Необходимо заметить, что номограмма пересчета используется в основном в зоне частот, где амплитудные характеристики параллельных звеньев близки друг к другу. В диапазоне частот, где характеристики существенно различаются, результирующая ЛАХ при согласном включении звеньев проходит по верхним участкам («по верхам») характеристик слагаемых звеньев, а при встречном их включении – по нижним участкам («по низам») ЛАХ охваченного звена и инверсной ЛАХ звена обратной связи. Физика такого явления заключается в том, что при согласном включении звеньев информация в основном передается через звено с большим коэффициентом усиления в рассматриваемом диапазоне частот. При встречном включении информация на выходе системы в зоне высоких частот определяется звеном, стоящим в прямом пути, а в зоне низких частот – звеном обратной связи.

В учебной практике приходится сталкиваться со случаями неудачного применения метода логарифмических частотных характеристик к расчету динамики САУ. Кажущаяся простота метода и отсутствие в нем формальных математических преобразований нередко является причиной использования данного метода для систем 2…3-го порядка, где более эффективным является применение других методов.

Дадим поэтому сравнительную характеристику линейных расчетно-аналитических методов исследование динамики САУ. Такое сравнение позволит оттенить достоинства и недостатки методов, подчеркнуть особенности каждого из них и наметить рациональные области их применения. Результаты такого анализа приведены в табл. 2.1.

Таблица 2.1.

Расчет динамики в t – области (классический метод)	Расчет динамики в р – области (операторный метод)	Расчет динамики в  - области (частотный метод)
ДОСТОИНСТВА
Высокая физическая наглядность Расчет не требует дополнительных формальных преобразований. Возможность экспериментального определения переходных характеристик	1. Использование алгебраических уравнений вместо дифференциальных 2. Автоматический учет ненулевых начальных условий и отсутствие необходимости определять постоянные интегрирования. 3. Универсальность метода.	1. Относительная простота синтеза САУ 2. Не возникает трудностей при переходе из -области в t-область 3. Возможность экспериментального определения АЧХ и ФЧХ
НЕДОСТАТКИ
Необходимо рассчитывать независимые начальные условия и производные переменных величин до n-1 порядка. Необходимо определять корни характеристического уравнения. 3. Нужно рассчитывать постоянные интегрирования.	1. Трудности перехода из р-области в t-область. Теорема разложения неприменима, если: а) неизвестны корни уравнения; б) функция не дробно-рациональная. 2. Недостаточная физическая наглядность. 3. Невозможность экспериментального определения передаточных функций.	Большой объем расчетно-графической работ. Невозможность расчета переходных процессов при возрастающих входных сигналах. Недостаточная наглядность.
ОБЛАСТЬ ПРИМЕНЕНИЯ МЕТОДОВ
САУ 1-го – 2-го порядка.	САУ 2-го – 3-го порядка.	САУ выше 3-го порядка.

2. Построение логарифмических частотных характеристик разомкнутых САУ

Передаточная функция системы при последовательном соединении звеньев равна произведению передаточных функций этих звеньев:

W(p)=W₁(p) W₂(p)... W_n(p),

где W_i(p) - передаточная функция звена, i=1,..n.

Тогда частотная передаточная функция системы:

W(j)=W₁(j) W₂(j)... W_n(j).

Представим частотную передаточную функцию звена в виде:

W_i(j)=A_i()e^ji().

Проведем подстановку и получим выражение:

W(j)=A₁()e^{ji1 ()}A₂()e^j2() ...A_n()e^jin()=A()e^j(),

где A()=A₁()A₂()...A_n(); ()=₁()+₂()+...+_n().

Найдем логарифмическую амплитудно-частотную характеристику системы:

L()=20lgA()=20lg(A₁()A₂()...A_n())=20lg A₁()+20lg A₂()+...+20lg A_n().

Как видно из формулы, логарифмическая амплитудная характеристика (ЛАХ) системы при последовательном соединении звеньев равна сумме логарифмических частотных характеристик этих звеньев.

Порядок построения ЛЧХ системы

1) на логарифмической оси частот наносятся точки, соответствующие сопрягающим частотам звеньев, входящих в систему (сопрягающая частота - это величина, обратно-пропорциональная постоянной времени звена);

2) если в передаточной функции системы W(p) имеются интегрирующие или дифференцирующие звенья типа Tp и(1/Tp), то построение результирующей ЛАХ начинается с них;

3) если в передаточной функции системы W(p) нет интегрирующего или дифференцирующего звена, то построение результирующей ЛАХ начинается с горизонтального участка, соответствующего коэффициенту усиления 20lgk,

k – общий коэффициент усиления системы;

4) наличие в передаточной функции звеньев типа (Tp+1) и (T²p²+2Tp+1) учитывается тем, что на соответствующих сопрягающих частотах ЛАХ претерпевает излом на величину n20дБ/дек (где n – порядок звена) вверх или вниз в зависимости от того, в числителе или в знаменателе передаточной функции W(p) находятся эти сомножители;

5) для построения логарифмической фазовой характеристики системы () необходимо построить частотные ЛФХ, соответствующие каждому сомножителю, а результирующая ЛФХ получается их геометрическим сложением.