Министерство образования РоссийскойФедерации

Санкт-Петербургский институт машиностроения (ЛМЗ-ВТУЗ)

Технологический факультет

Кафедра электротехники, вычислительной техники и автоматизации

ПРАКТИКУМ ПО ТЕОРИИ АВТОМАТИЧЕСКОГО УПРАВЛЕНИЯ

Часть 1

Методические указания

к самостоятельной работе студентов

Санкт-Петербург 2003

Практикум по теории автоматического управления: Метод. указания к самостоятельной работе студентов. –СПб.: ПИМаш, 2003. – 56 с.

Рассмотрены теоретические основы и практические аспекты применения структурно-топологических методов преобразования динамических моделей САУ и частотных методов исследования линейных и нелинейных систем. Ориентированы на самостоятельную работу студентов, содержат большое количество примеров и задания по указанным частям курса.

Составители: д-р техн. наук, проф. В.М. Шестаков, к.т.н. О.Л. Нагибина, к.т.н., доц. О.П. Томчина

Методические указания утверждены на заседании кафедры электротехники, вычислительной техники и автоматизации

Научный редактор - д-р. техн. наук, проф. Шестаков В.М.

Рецензенты: д-р техн. наук, проф. А.Л. Фрадков

к. т. н., доц. В.И. Репкин

Редактор - Г.Л. Чубарова

П21(03)

Подписано в печать 19.03.2003. Формат 60х90 1/16.

Бумага тип. №3. Печать офсетная. Усл.печ.л 3,5.

Уч.-изд.л. 3,5. Тираж 300 экз. Заказ № 9.

Издание Санкт – Петербургского института машиностроения

195197, Санкт – Петербург, Полюстровский пр.,14

ОП ПИМаш

Глава 1. Топологические преобразования

динамических структурных моделей САУ

1.1. Получение передаточных функций САУ путем структурных преобразований моделей систем

1. Пусть звенья системы соединены последовательно:

W₁ (p)

U

W₂ (p)

W_n (p)

(р) y₁(р) y ₂ (р) y_n-1(р) y_n(р)

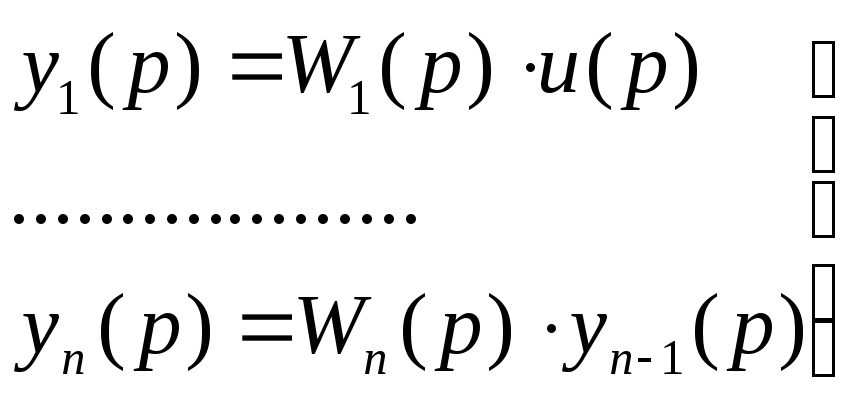Система уравнений звеньев, включенных последовательно, имеет следующий вид:

После исключения промежуточных переменных имеем:

Таким образом, передаточная функция последовательно включенных звеньев равна произведению их передаточных функций.

2. Пусть звенья системы соединены параллельно:

W₁ (p)

y₁(p)

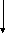
u(p) y₂ (p) y(p)

W₂(p)

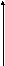
y_n(p)

W_n (p)

В этом случае система уравнений звеньев, включенных параллельно, имеет вид:

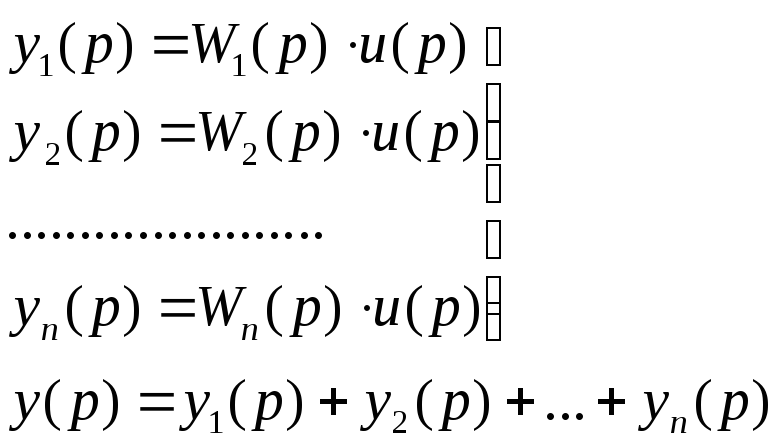
Проведя необходимые подстановки в последнее уравнение, получим, что передаточная функция такой системы равна сумме передаточных функций звеньев, входящих в соединение:

3. Звено, охваченное обратной связью.

Обратная связь может быть положительной, если сигнал обратной связи складывается с входным сигналом, или отрицательной, если сигнал обратной связи вычитается из входного сигнала:

U(p) y(p)

W₁(p)

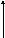
y_oc(p)

W_oc(p)

Схема описывается следующими уравнениями:

После преобразования получим:

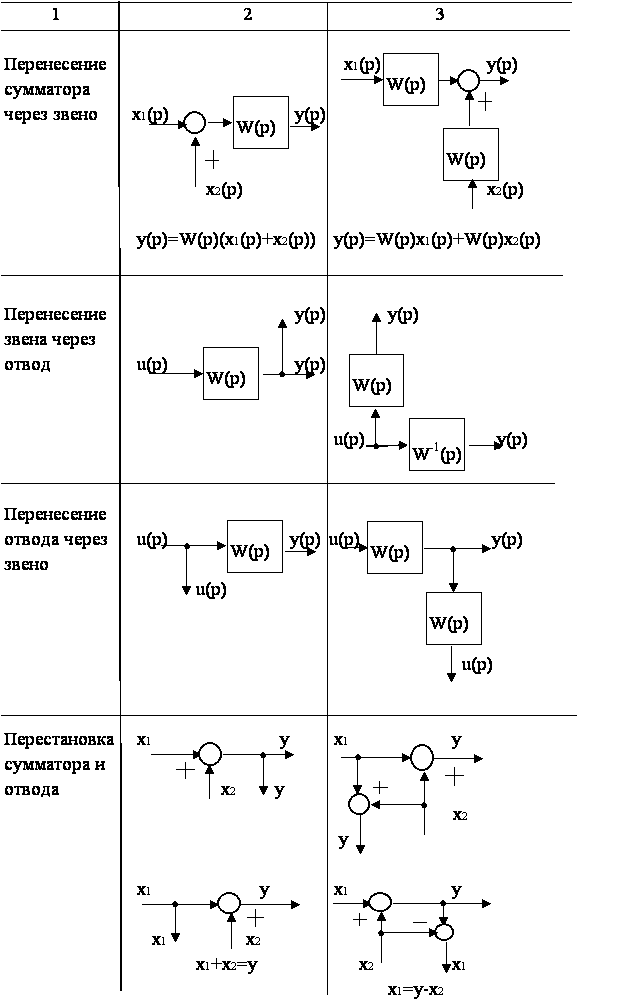
Таблица 1.1

Правила эквивалентных структурных преобразований

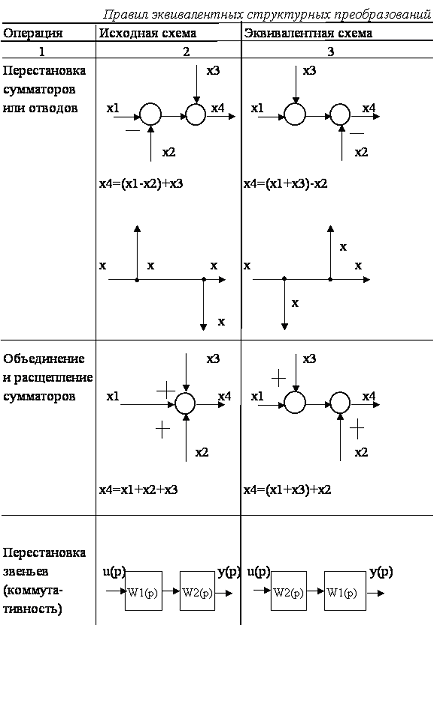
Продолжение табл. 1.1

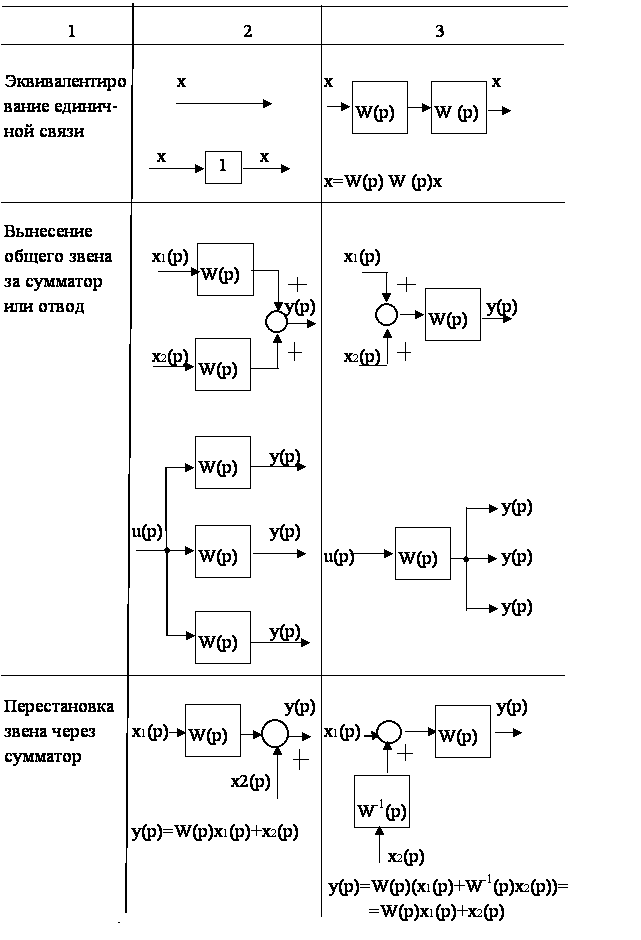
Окончание табл. 1.1

Рассмотрим пример 1.

W₅(p)

U

W₃(p)

W₄(p)

W₆(p)

(p) y(p)

W₁(p)

W₂(p)

Чтобы получить передаточную функцию системы, необходимо начать с внутренних локальных контуров и связей, не пересекающихся с другими связями. Для данной схемы сначала целесообразно свернуть участок схемы сW₁(р) и W₂(р). Звенья соединены встречно-параллельно (соединение с отрицательной обратной связью). Следовательно, передаточная функция локального контура будет иметь вид:

Звенья W₄(p) и W₅(p) соединены параллельно, следовательно передаточная функция соединения имеет вид:

W₈ (р)=W₄ (р)+W₅(р).

Тогда исходная структурная схема примет следующий вид:

u(р) y(р)

W₇(р)

W₃(р)

W₆(р)

W₈(р)

Для дальнейшей свертки структурной схемы необходимо избавиться от перекрещивающихся связей.

Воспользуемся правилом перестановки отвода и звена (W₆); получим структурную схему в виде:

W₆^-1(р)

U(р) y(р)

W₇(р)

W₃(р)

W₈(р)

W₆(р)

Далее воспользуемся правилом перестановки звена W₇(р) и сумматора, одновременно используя правило перестановки сумматоров. Таким образом, получена структурная схема в следующим виде:

W₆^-1(р)

W₇^-1(р)

U(р) y(р)

W₇(р)

W₃(р)

W₈(р)

W₆(р)

Как видно из рисунка, данная схема не содержит перекрещивающихся связей. Пары звеньев W₇–W₃ и W₈–W₆ соединены последовательно, поэтому структурную схему можно упростить, если ввести в рассмотрение передаточные функции:

W₉ (р)=W₇ (р)W₃(р), W₁₀ (р)=W₈ (р)W₆(р).

При этом схема примет вид:

W₆^-1(р)

W₇^-1(р)

U(р) y (р)

W₉(р)

W₁₀(р)

ЗвеньяW₉ (р) и W₁₀(р) охвачены единичной обратной связью. Свернем эти локальные контуры и получим передаточные функции:

Таким образом, полученная структура имеет один контур:

W₆^-1(р)

W₇^-1(р)

u (р) y(р)

W11(р)

W₁₂(р)

Передаточная функция этого контура, а следовательно, и всей системы будет: