Архимедовская расположенность поля действительных чисел.

Теорема 5. Поле действительных чисел архимедовски расположенное, т.е. выполняется аксиома Архимеда: .

Доказательство.

Пусть . Последнее означает, что

- положительная, следовательно, .

- ф.п.р.ч., следовательно, - ограниченная, тогда следовательно,. Поскольку поле рациональных чисел архимедовски расположенное,.

.

что и требовалось доказать.

Теорема 6. Поле действительных чисел является всюду плотным.

Доказательство.

Пусть . Для определенности положим, что. Тогда- положительная, следовательно,. Поскольку,- ф.п.р.ч, имеем

. Возьмем . Учитывая выше изложенное, получим

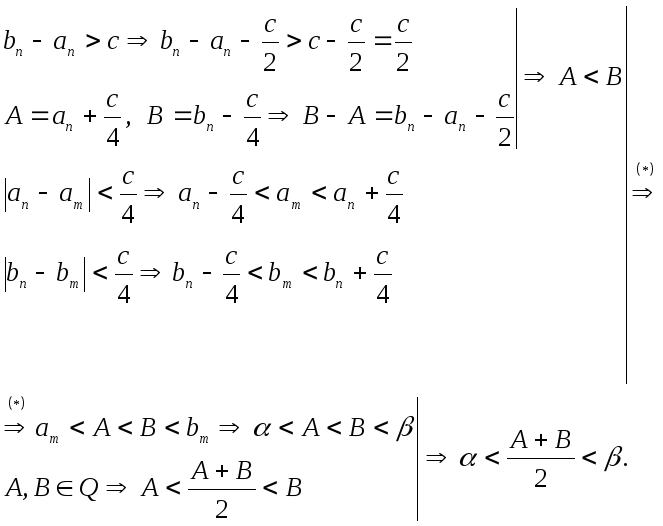
что и требовалось доказать.

Теорема о сходимости любой фундаментальной последовательности рациональных чисел в поле действительных чисел.

Теорема 7. т.т.т., к., иными словами всякая фундаментальная последовательность рациональных чисел сходится в поле действительных чисел.

Доказательство.

Необходимость.

Пусть . Возьмемтакое, что, где(в силу фундаментальности последовательности). Тогда. Согласнолеммам 1, 2, имеем, что , следовательно,. Таким образом,.

Достаточность.

Пусть . Покажем, что- ф.п.р.ч.

. Поскольку между действительными числами инайдется положительной рациональное число. Тогда. Оценим, где:

. Таким образом, последовательность рациональных чисел фундаментальна, а, значит, порождает некоторый класс эквивалентности. Остается доказать, что. Возможны случаи:

1. .

Последнее противоречит условию , следовательно, данный случай невозможен.

2. .

Последнее противоречит условию , следовательно, данный случай невозможен.

3. . Единственно возможный случай.

что и требовалось доказать.

Следствие. Для того, чтобы последовательность рациональных чисел имела в поле действительных чисел предел необходимо и достаточно, чтобы она была фундаментальной.

Теорема о сходимости любой фундаментальной последовательности действительных чисел в поле действительных чисел.

Теорема 8. Любая фундаментальная последовательность действительных чисел сходится в поле действительных чисел.

Доказательство.

Пусть - ф.п.д.ч., где :

Рассмотрим последовательность . Покажем, что она фундаментальна.

Последнее неравенство влечет фундаментальность последовательностей вида при фиксированном. Оценим теперь:

. Таким образом, последовательность фундаментальна. Докажем, чтои есть предел последовательности. Пусть.

Последнее неравенство доказывает, что .

что и требовалось доказать.

Лекция 10. Поле комплексных чисел.

Возможны различные подходы к определению поля комплексных чисел.

Один из возможных заключается в следующем:

Определение. Полем комплексных чисел называется алгебраическое расширение поля действительных чисел, иначе, поле комплексных чисел наименьшее из полей, содержащее все алгебраические элементы над полем действительных чисел (т.е. все корни многочленов с действительными коэффициентами).

В этом случае , где- корень многочлена.

Другой подход основан на построении поля комплексных чисел как подкольца кольца квадратных матриц второго порядка над полем действительных чисел.

Рассмотрим множество .- кольцо. В этом кольце выбирается подмножество.

Теорема 1. - поле.

Доказательство.

Проверим, что подкольцо кольца, а, следовательно, само образует кольцо.

.

Нетрудно устанавливается, что в умножение коммутативно и ассоциативно.

Остается покакать, что в каждый ненулевой элемент обратим.

Пусть - обратима в. Тогда.

Таким образом, - поле.

что и требовалось доказать.

Теорема 2. Поле действительных чисел изоморфно вкладывается в поле комплексных.

Доказательство.

Рассмотрим соответствие по правилудля всех.

Очевидно, что - всюдуопределено и однозначно, а, следовательно,- отображение.

- инъективное отображение.

Покажем, что - гомоморфизм.

Таким образом, - инъективный гомоморфизм, а, значит,изоморфно вкладывается в.

что и требовалось доказать.