Основы инженерного творчества(Суздальцев А.И

пень интеграции, быстродействие и надѐжность электронных систем, одновременно снижая их энергопотребление.

Но переход на микроуровень характерен не только для электронных систем, но и для многих других технических систем. Вместо механической обработки материалов и изделий всѐ шире применяется химическая, ионная и плазменная обработка, обработка квантами электромагнитного излучения (лазерная) и т.п. Одним из новейших и бурно развивающихся современных направлений научнотехнического прогресса является развитие нанотехнологии и нанотехники, которые определяют переход на микроуровень не только электронных, но и других систем разнообразного назначения. Нанотехнология представляет собой технологические процессы, базирующиеся на манипулировании отдельными атомами и молекулами вещества. По мнению многих экспертов, именно нанотехнология является путѐм к третьей научно-технической революции, которая уже начинает разворачиваться. Уже сейчас основанные на нанотехнологии сканирующие туннельные микроскопы (СТМ), имеющие разрешение, сопоставимое с размерами отдельных атомов, позволили расшифровывать строение молекул ДНК и составляющих их геномов, «ремонтировать» и изменять их, т. е. создали мощный инструментарий для генной инженерии.

С помощью нанотехнологии получены новые материалы – фуллерены и нанотрубки. Фуллерены – это молекулы углерода, состоящие из расположенных в виде сферы 60 атомов углерода, которые сами по себе обладают уникальными свойствами, но помимо этого являются ещѐ основой для получения нанотрубок, в которых атомы углерода располагаются не в виде сферы, а в виде трубок с одноатомными стенками. Такие трубки могут состоять из миллионов атомов углерода, связанных в единую молекулу. Причем межатомное пространство в полости этих трубок может заполняться атомами других веществ, придающих таким трубкам новые свойства. Специалисты предсказывают, что уже во втором десятилетии нынешнего столетия будут созданы первые нанокомпьютеры и примерно к этому же времени появится возможность создания самовоспроизводящихся нанобиороботов (по типу искусственных микробов), которым можно поручать ремонт отдельных клеток в биологическом организме и другие работы. Основными направлениями развития нанотехнологии и нанотехники являются: наномеханика и наномашиностроение, создание новых наноматериалов, и наноэлектроника, в том числе разработка нанотранзисторов и на их основе нанокомпьютеров, нанооптика, в том числе разработка графически перестраиваемых лазеров, нанобиоло-

120

гия и наномедицина. Все эти направления и будут составлять суть грядущей третьей научно-технической революции.

Таким образом, именно переход на микроуровень является наиболее кардинальным средством приближения к идеальной системе. Даже в вышеприведѐнном фантастическом примере идеальной системы (полѐты Ариэля) система работает на микроуровне, управляя направлением теплового движения атомов и молекул, из которых состоит тело человека.

Одним из следствий этого закона является развитие технических систем в направлении увеличения степени вепольности.

3.1.10.Закон увеличения степени вепольности системы

Развитие технических систем идѐт в направлении увеличения степени вепольности. Смысл этого закона заключается в том, что невепольные системы стремятся стать вепольными, а в вепольных системах развитие идѐт в направлении перехода от механических полей к электромагнитным и далее к ферромагнитным. Подробнее этот вопрос рассматривается в подразделе 3.2.6.

3.2. Алгоритм решения изобретательских задач

3.2.1. Общая структура алгоритма

Рассмотрение АРИЗ можно начать с высказывания: «Ковыляющий по прямой дороге опередит бегущего, который сбился с пути (Ф. Бэкон)».

Прямую дорогу к изобретению, по которой не нужно ковылять, указывает АРИЗ, который как и весь ТРИЗ находится в развитии [21,22,24]. Известны следующие редакции АРИЗ: АРИЗ-59, АРИЗ-61, 64, 65, 68, 71, 75, 77, 82, 85. Ниже рассматривается один из базовых – АРИЗ-77, структура которого приведена на рис. 3.4.

121

ТАТА

3

Рис. 3.4. Структура алгоритма решения изобретательских задач

Он включает семь больших последовательно выполняемых шагов со своими маленькими шагами (подшаги). Каждый большой шаг представлен в виде геометрической фигуры с количеством углов, равным количеству подшагов в соответствующем шаге. Названия больших шагов приведены на рисунке, а названия подшагов и их действия с примерами описаны подробно в известной книге Г.С. Альт-

122

шуллера «Творчество как точная наука» [2]. Алгоритм изобилует множеством специальных операторов, которые рассматриваются ниже.

3.2.2. Специальные операторы АРИЗ

В соответствии со структурой алгоритма в процессе решения задачи на отдельных шагах алгоритма используются специальные операторы: РВС (размер – время – стоимость); ТП (техническое противоречие); ИКР (идеальный конечный результат); ММЧ (моделирование с помощью маленьких человечков); ФП (физическое противоречие); ВА (вепольный анализ); ПУТП (приѐмы устранения технических противоречий); ФЭЯ (физические эффекты и явления); СТРИЗ (стандарты решения изобретательских задач).

3.2.3. Оператор РВС

РВС – это размеры, время, стоимость. Любая техническая система, данная в условиях задачи, имеет привычный для нас образ. Можно, например, убрать из текста задачи слово «ледокол», но останется образ ледокола: нечто «кораблеобразное», примерно соответствующее по размерам ледоколу, действующее примерно в таком же темпе и стоящее примерно столько же. Термина уже нет, но образ исходной системы сохранился и несет сильный заряд психологической инерции. Цель оператора РВС — преодолеть эту инерцию, сломать навязчивый старый образ технической системы. Оператор РВС включает шесть мысленных экспериментов, перестраивающих условия задачи (шаг 1.9 в тексте АРИЗ-77). Эксперименты могут быть осуществлены на разных уровнях – тут многое зависит от силы воображения, от характера задачи и от других обстоятельств. Однако даже формальное выполнение этих операций резко сбивает психологическую инерцию, связанную с привычным образом системы данного пособия.

3.2.4. Оператор ИКР

Смысл этой операции заключается в том, чтобы получить

ориентир для перехода к сильным решениям. Идеальное решение

123

наиболее сильное из всех мыслимых и немыслимых решений.

Это как бы решение не существующего шестого уровня. Тактика решения задачи с помощью ИКР состоит в том, чтобы уцепиться за этот сверхсильный вариант и по возможности меньше от него отступать. ИКР формулируют по простой схеме: один из элемен-

тов конфликтующей пары сам устраняет вредное действие, со-

храняя способность осуществлять основное действие. Идеаль-

ность решения обеспечивается тем, что нужный эффект достига-

ется даром, без использования каких бы то ни было средств.

Например для задачи 1 ИКР можно записать так: Тепловое поле

само предотвращает порчу проволоки, обеспечивая тем не менее требуемое тепловое удлинение. Что может быть идеальнее? Ни-

чего не ввели, ничего не усложнили, но вредное действие тепло-

вого поля словно по волшебству исчезло, а полезное действие со-

хранилось. Дикость, парадоксальность, возникшая уже при пере-

ходе к модели задачи, резко усиливается. Тепловое поле должно не только осуществлять несовместимые действия, но и делать это само – без всяких машин, механизмов и прочих устройств. Пере-

ход к ИКР отсекает все решения низших уровней, отсекает без перебора и сразу.

3.2.5 Оператор ММЧ

Есть много тонких механизмов решения, которые сегодня еще нельзя сформулировать в виде простых правил. Они пока не включены в текст АРИЗ, но их можно «встроить» по усмотрению преподавателя, когда обучающиеся привыкнут вести анализ, не обрывая его где-то в середине извечным: «А что если сделать так?..». Гордон, создавая синектику, дополнил мозговой штурм четырьмя видами анало-

124

гий, в том числе эмпатией – личной аналогией. Сущность этого приема заключается в том, что человек решающий задачу, «входит» в образ совершенствуемого объекта и старается осуществить требуемое задачей действие. Если при этом удается найти какой-то подход, ка- кую-то новую идею, решение «переводится» на технический язык. «Суть эмпатии, – писал Дж. Диксон, – состоит в том, чтобы «стать» деталью и посмотреть с ее позиции и с еѐ точки зрения, что можно сделать» [8]. Дж. Диксон считал, что этот метод очень полезен для получения новых идей.

Практика применения эмпатии при решении учебных и производственных задач показывает, что эмпатия действительно иногда бывает полезна. Но иногда она бывает и очень вредна. Почему?

Отождествляя себя с той или иной машиной (или ее частью) и рассматривая ее возможные изменения, изобретатель невольно отбирает те, которые приемлемы для человека, и отбрасывает неприемлемые для человеческого организма, например разрезание, дробление, растворение в кислоте и т. д.

Неделимость человеческого организма мешает успешно применять эмпатию при решении многих задач, подобных, например, задачам 1 – 9.

Недостатки эмпатии устранены в моделировании с помощью маленьких человечков (ММЧ) – методе, который применяется в АРИЗ. Суть его состоит в том, чтобы представить объект в виде множества («толпы») маленьких человечков. Такая модель сохраняет достоинства эмпатии (наглядность, простота) и не имеет присущих ей недостатков.

В истории науки известны случаи, когда стихийно применялось нечто похожее на ММЧ. Два таких случая особенно интересны. Первый – открытие Кекуле структурной формулы бензола.

«Однажды вечером будучи в Лондоне, – рассказывает Кекуле, – я сидел в омнибусе и раздумывал о том, каким образом можно изобразить молекулу бензола С6Н6 в виде структурной формулы, отвечающей свойствам бензола. В это время я увидел клетку с обезьянами, которые ловили друг друга, то схватываясь между собой, то опять расцепляясь, и один раз схватились таким образом, что составили кольцо. Каждая одной задней рукой держалась за клетку, а следующая держалась за другую ее заднюю руку обеими передними, хвостами же они весело размахивали по воздуху. Таким образом, пять обезьян, схватившись, образовали круг, и у меня сразу же блеснула в го-

125

лове мысль: вот изображение бензола. Так возникла вышеприведенная формула, она нам объясняет прочность бензольного кольца» [2].

Второй случай еще более известен. Это мысленный эксперимент Максвелла при разработке им динамической теории газов. В этом мысленном опыте были два сосуда с газами при одинаковой температуре. Максвелла интересовал вопрос, как сделать, чтобы в одном сосуде оказались быстрые молекулы, а в другом медленные. Поскольку температура газов одинакова, сами по себе молекулы не разделятся: в каждом сосуде в любой момент времени будет определенное число быстрых и медленных молекул. Максвелл мысленно соединил сосуды трубкой с дверцей, которую открывали и закрывали «демоны» – фантастические существа примерно молекулярных размеров. Демоны пропускали из одного сосуда в другой быстрые частицы и закрывали дверцу перед маленькими частицами.

Два этих случая интересны, прежде всего тем, что объясняют, почему в ММЧ взяты именно маленькие человечки, а не, например, шарики или микробы. Для моделирования нужно, чтобы маленькие частицы видели, понимали, могли действовать. Эти требования естественнее всего ассоциируются с человеком: у него есть глаза, мозг, руки. Применяя ММЧ, изобретатель использует эмпатию на микроуровне. Сохранена сильная сторона эмпатии и нет присущих ей недостатков.

Эпизоды с Кекуле и Максвеллом описывались многими авторами. Но никто не связывал их вместе и не задумывался над вопросом: почему бы не превратить эти случаи в метод, используемый сознательно? Историю с Кекуле обычно приводили, чтобы поговорить о роли случайности в науке и изобретательстве.

А из опыта Максвелла делали и без того очевидный вывод, что ученому нужно воображение.

Техника применения метода ММЧ сводится к следующим операциям:

-на шаге 3.3 АРИЗа надо выделить часть объекта, которая не может выполнить требования, указанные на шаге 3.2, и представить эту часть в виде маленьких человечков;

-надо разделить человечков на группы, действующие (перемещающиеся) по условиям задачи;

-полученную модель надо рассмотреть и перестроить так, чтобы выполнялись конфликтующие действия.

126

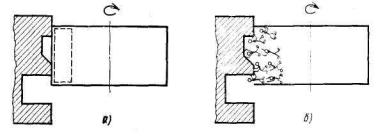
Например, в задаче 8 («Даны круг и изделие. Круг обладает способностью шлифовать, но не может приспосабливаться к криволинейной поверхности изделия») рисунок к шагу 3.3 обычно выглядит так, как показано на рис. 3.5,а: выделен внешний слой круга, который по структуре ничем не отличается от центральной части круга. На рис. 3.5,б показан тот же рисунок, но сделанный с использованием ММЧ. Маленькие человечки, соприкасающиеся с обрабатываемой поверхностью, удаляют частицы металла, а другие человечки придерживают «работников», не давая им вылететь из круга, упасть, быть отброшенными. Меняется глубина впадины – соответственно перестраиваются человечки. Рассматривая левый рисунок, не так просто прийти к выводу о необходимости раздробить наружную часть на «зерна», сделав эти зерна подвижными и в то же время «цепляющимися» за круг. Правый рисунок приводит к этой идее.

Рис. 3.5. Использование метода ММЧ к задаче 8

Однажды на семинаре по ТРИЗ слушателям была предложена задача об увеличении скорости движения ледокола (задача 9): повысить скорость за счет увеличения мощности двигателей нельзя; современные ледоколы настолько «заполнены» двигателями, что почти не несут полезной нагрузки (подробные условия задачи и запись решения по АРИЗ [1].

Сначала задачу решали, используя эмпатию. Один из слушателей, вживаясь в «образ ледокола», сосредоточенно ходил по комнате, а потом подошел к столу. «Это – лед, – сказал слушатель. – А я – ледокол. Я хочу пройти сквозь лед, но лед меня не пропускает...» Он давил на «лед», наскакивал на него с разбега, временами ноги «ледокола» пытались пройти под столом, но туловище этому мешало, иногда туловище пыталось пройти над столом, но мешали ноги... Отождествив себя с ледоколом, слушатель перенес на ледокол неделимость,

127

присущую человеческому организму, и тем самым усложнил задачу, эмпатия в данном случае только затрудняла решение.

На следующем занятии тот же слушатель решал задачу, используя метод ММЧ. Он подошел к столу, несколько секунд подумал, потом с некоторой растерянностью сказал: «Не понимаю, в чем задача... Если я состою из толпы маленьких человечков, верхняя половина толпы пройдет над столом, нижняя – под столом... По-видимому, задача теперь в том, как соединить две части ледокола – надводную и ту, что подо льдом. Придется ввести какие-то стойки, узкие, острые, они легко пройдут сквозь лед, не надо будет ломать огромную массу льда...»

Метод ММЧ еще не исследован до конца, в нем много загадочного. Скажем, в задачах на измерение длины выделенную часть элемента лучше представлять не в виде сплошной шеренги человечков, а как шеренгу «через одного». Еще лучше, если человечки расположены в виде треугольника. И еще лучше – неправильным треугольником (с неравными или криволинейными сторонами). Почему? Пока тут можно только строить догадки. Но правило действует.

Пусть дана задача 10: «Нужно с самолета измерить глубину реки через каждые 300 – 500 м на протяжении 100 км. Никакого специального оборудования на самолете нет, высадка людей исключена, измерение надо провести предельно дѐшево. Точность измерения ± 0,5 м. Скорость течения неизвестна. Как быть? По условиям задачи вертолет применить нельзя, высадка людей недопустима, использовать ка- кие-нибудь свойства радиоволн тоже нельзя, потому что нет возможности заказывать специальное оборудование. К тому же замеры глубины надо выполнить в сущности бесплатно (допустимы только расходы на оплату полета вдоль реки)».

Используем метод ММЧ. Еще неизвестная «измерялка», которую придется использовать, бросив или направив с самолета, должна иметь форму неправильного треугольника. Мыслимы только два варианта расположения маленьких человечков (рис. 3.6), образующих эту «измерялку».

128

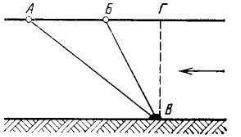
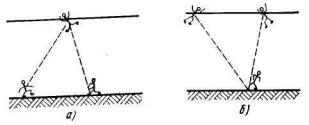
Рис. 3.6. Иллюстрация метода ММЧ к задаче 10

Верхние человечки должны быть легче воды, нижние – тяжелее. Предположим, что это деревяшки и камни, объединенные леской (рис. 3.7). Реализовать такой треугольник нетрудно. Деревяшки А и Б соединены с камнем В лесками, причем длины обеих лесок заведомо превышают глубину реки (это можно проверить пробным сбросом). Чем глубже река, тем меньше расстояние АБ (деревяшки не связаны между собой). К одному из поплавков надо прикрепить (для «масштаба») метровую рейку, и можно сбрасывать это «оборудование», а затем фотографировать сверху. Зная АВ и БВ и измерив на снимке АБ, легко вычислить ВГ. Решение удивительно простое и красивое (а. с.

СССР № 180815). Прийти к нему без подсказки («Сбрось трех человечков, прикажи им расположиться в виде неправильного треугольника...») очень трудно, в чѐм можно убедиться предложив решить задачу тому, кто не знаком с методом ММЧ.

Рис. 3.7. Иллюстрация метода

Рассмотрим теперь задачу 11, в которой речь идет об измерении радиуса шлифовального круга, поэтому здесь тоже должны помочь маленькие человечки. Металлический цилиндр обрабатывается изнутри образивным кругом. В процессе работы круг истирается. Как измерить диаметр круга, не прерывая шлифовки и не выводя круг из цилиндра?

Если на торец круга нанести электропроводную полоску и пропускать ток, то по изменению сопротивления можно судить об изменении радиуса круга (рис. 3.8, а). К сожалению, такая схема не обеспечивает точность измерений. Сопротивление зависит не только от длины полоски, но и от силы прижатия круга к обрабатываемой поверхности и от состояния контакта «цепь – вал», и от температуры круга.

Попробуем расположить маленьких человечков цепочкой «через одного» (рис. 3.8, б). Теперь об измерении радиуса круга можно су-

129