2. Задача 16.

Составить уравнения касательной и нормали к кривой в точке, соответствующей значению параметра .

Уравнения касательной и нормали к кривой, заданной параметрически, запишутся соответственно в виде:

,

, где

- координаты точки кривой,

- координаты произвольной точки касательной.

Пример.

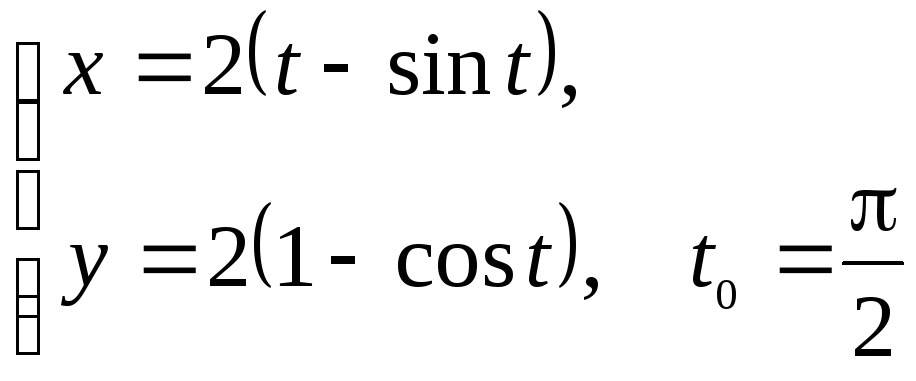
Решение:

1. Найдем значения 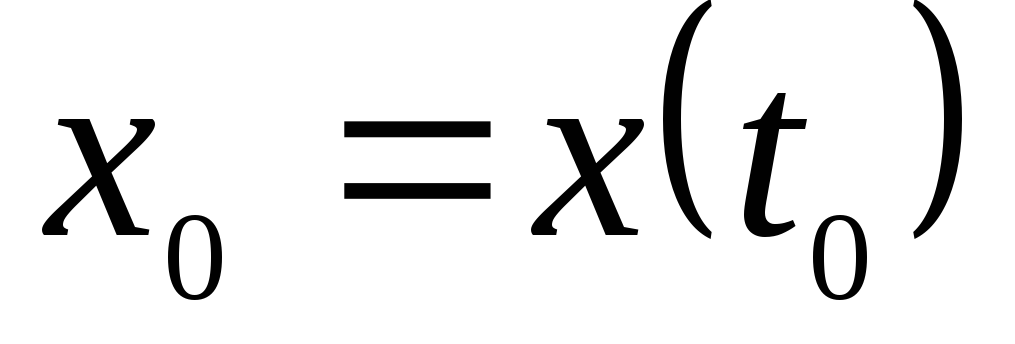и

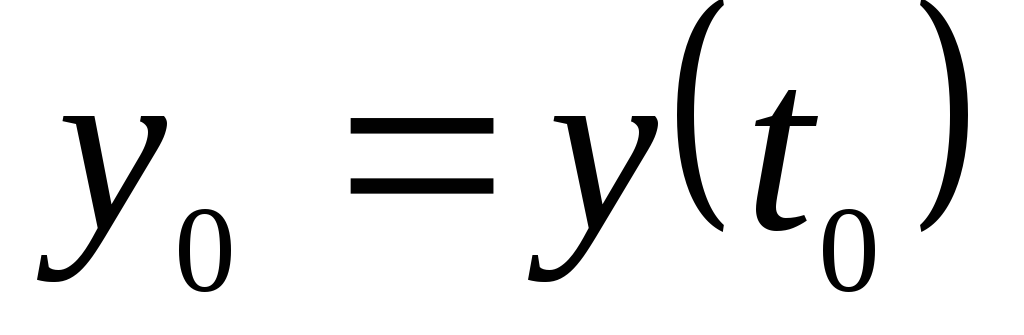
2. Находим производную 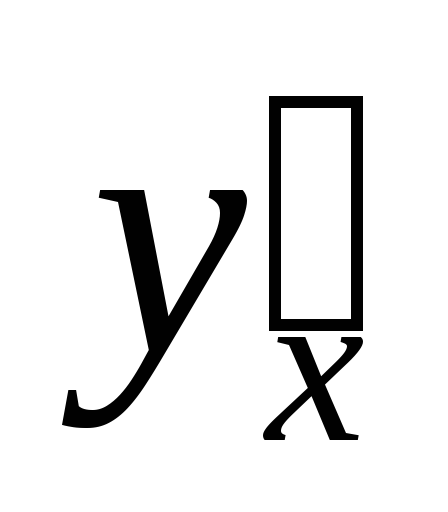по формуле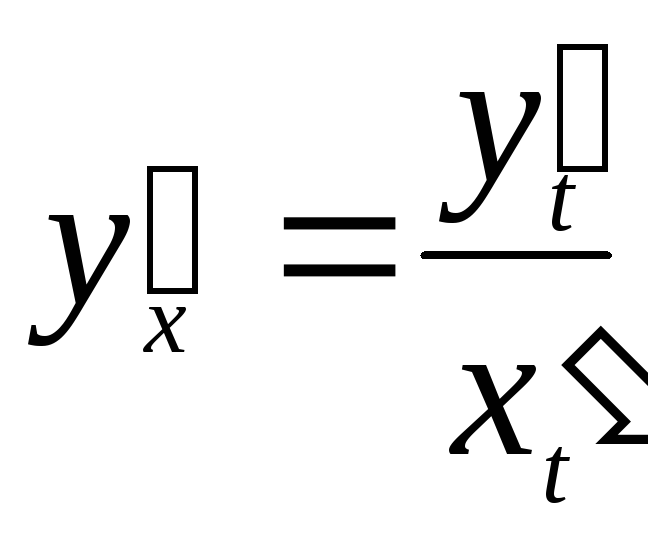

,

а затем ее значение при

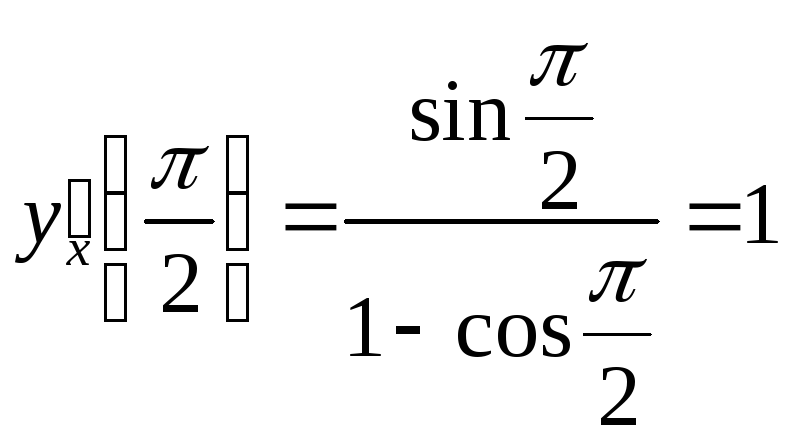
3. Подставляя значения 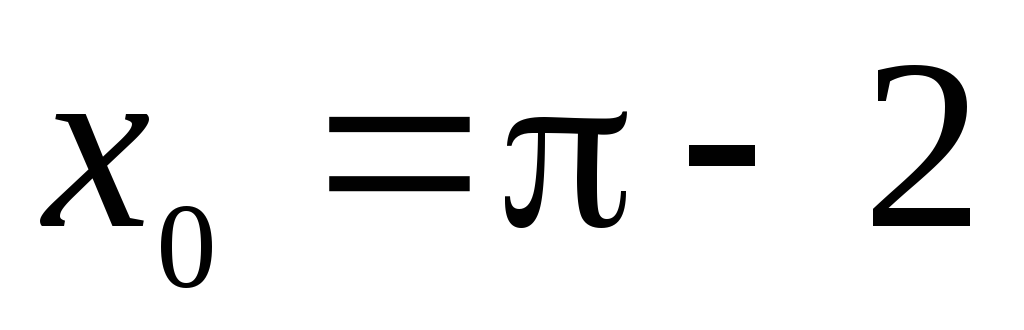,,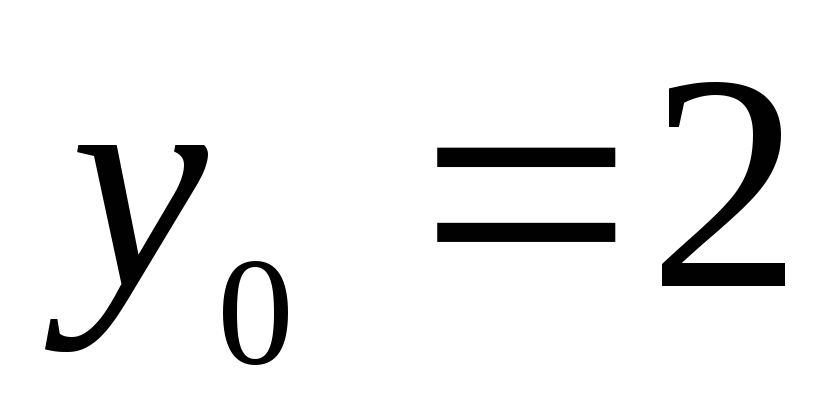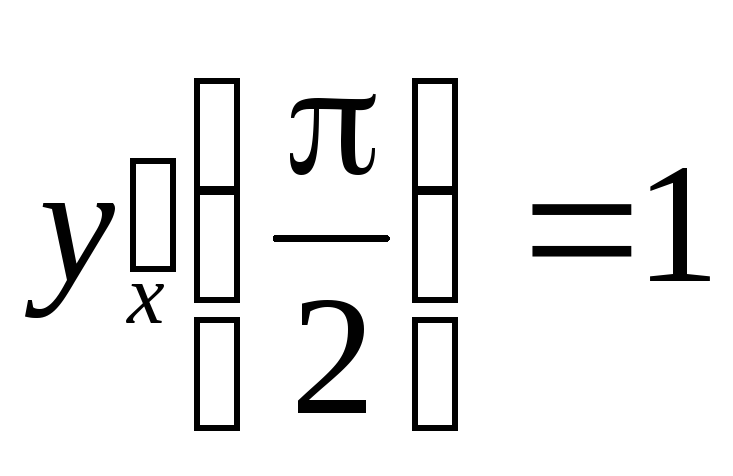в формулу (3) и (4), получаем соответственно уравнения касательной и нормали к данной кривой в точке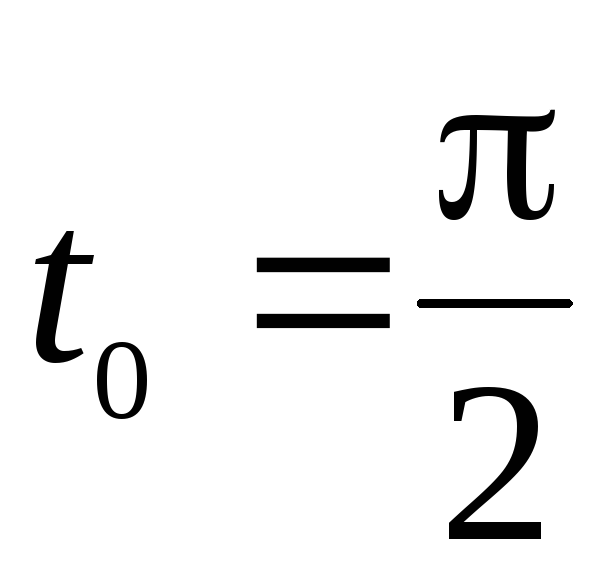

- уравнение касательной

- уравнение нормали.

Ответ: - уравнение касательной

- уравнение нормали.

7. Приложение производной

   1. Задача 20.

Покажите, что функция y удовлетворяет заданному уравнению.

Используя приложения А, Б и основные правила вычисления производных, дифференцируем заданную функцию. Затем, подставляя данную функцию y и найденную производную в левую часть заданного уравнения и произведя тождественные преобразования, получаем правую часть исходного уравнения.

Пример 1. ,(5)

Решение: Найдем производную, используя правило нахождения производной частного:

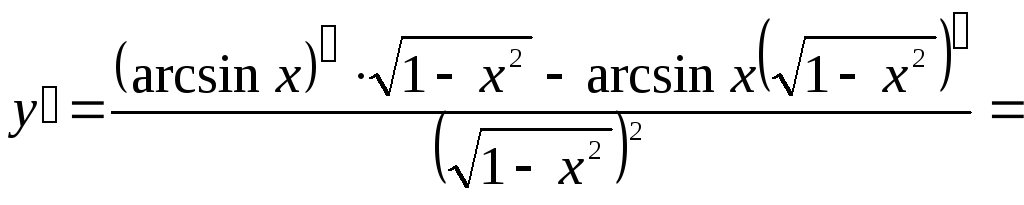
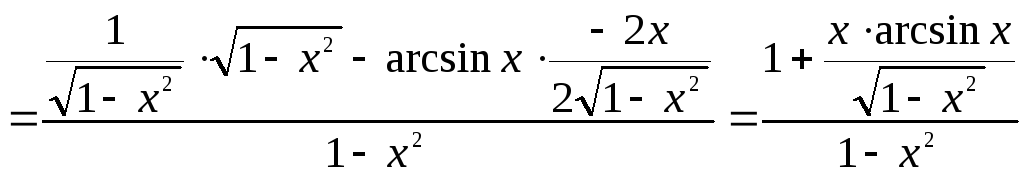
Подставим y и в левую часть уравнения (1)

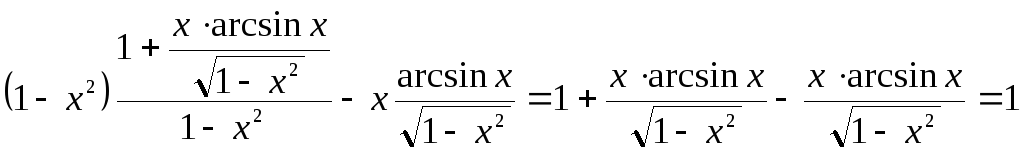
Получили правую часть уравнения (5).Значит, функция y удовлетворяет уравнению (5), что и требовалось.

Пример 2. (6)

Решение: Находим производную

Подставим y и в левую часть уравнения (1)

Получили правую часть уравнения (6).Значит, функция y удовлетворяет уравнению (6), что и требовалось.

Литература

1. Бермант А.Ф. Краткий курс математического анализа. / Араманович И.Г. - М.: Наука, 1969.

2. Виленкин Н.Я. Математический анализ. / Мордкович А.Г.

3. Кудрявцев Л.Д. Курс математического анализа. – М.: Высшая школа, 1988.

4. Фихтенгольц Т.М. Курс дифференциального и интегрального исчисления. – Т.1. – М.: Физматгиз, 1962.

5. Гусак А.А. Пособие к решению задач по высшей математике. – Мн. Изд. БГУ, 1973.

6. Данко П.Е. Высшая математика в упражнениях и задачах. / Попов А.Г., Кожевникова Т.Я. – М.: Наука, 1986.

7. Запорожец Г.И. Руководство к решению задач по математическому анализу. – М.: Высшая школа, 1964.

8. Сборник задач по математическому анализу под редакцией Демидовича Б.П. – М: Наука, 1978.

9. Кузнецов Л.А. Сборник заданий по высшей математике (ТР) – М.: Высшая школа, 1983.

10. Бронштейн И.Н. Справочник по математике для инженеров и учащихся ВТУЗов / Семендяев К.А.– м.: Наука, 1982.

Приложение а

Таблица производных основных элементарных и сложных функций.

Таблица 1

1. Степенная функция:
2. Показательная функция:
3. Логарифмическая функция:
4. Тригонометрические функции:
5. Обратные тригонометрические функции:
6. Гиперболические функции

Приложение б

Таблица производных n-го порядка некоторых функций.

Таблица 2

Функция	Производная n-го порядка

39