
Задача 12.
Найдите производную.
Пример.
![]()
Решение: Составим схему структуры данного выражения (рис 7)
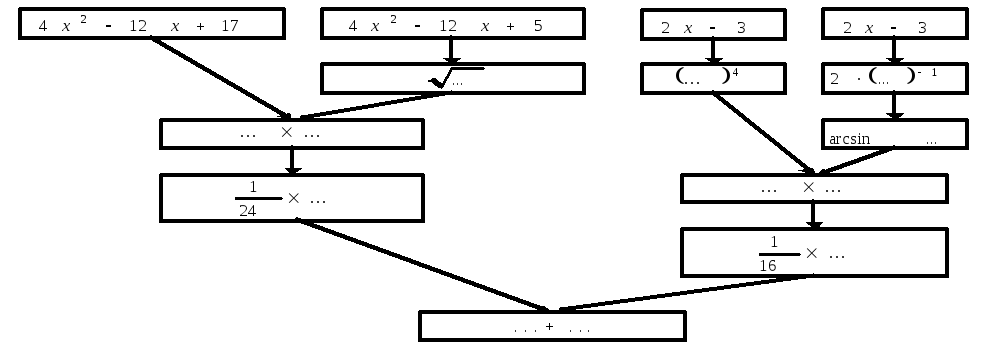
Рис. 7 Схема
![]()
![]()
![]()
![]()
![]()

![]()

![]()
![]()
![]()
![]()
![]()
![]()
Ответ:
![]()
Задача 13.
Найдите производную.
Пример.
![]()
Решение:
![]()
Воспользуемся схемой структуры данной функции (рис. 8).
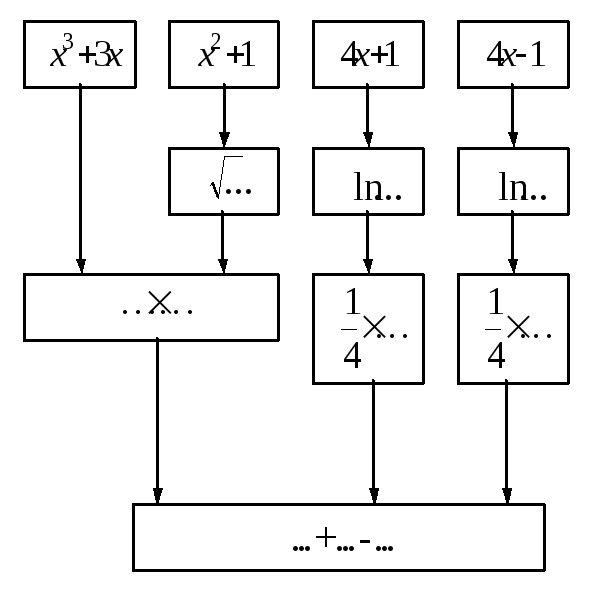
Рис. 8 Схема
![]()
![]()
![]()
![]()
![]()
![]()
Ответ:
![]()
Задача 14.
Найдите производную.
Пример.
![]()
Решение: Составим схему структуры данной функции (рис. 9)
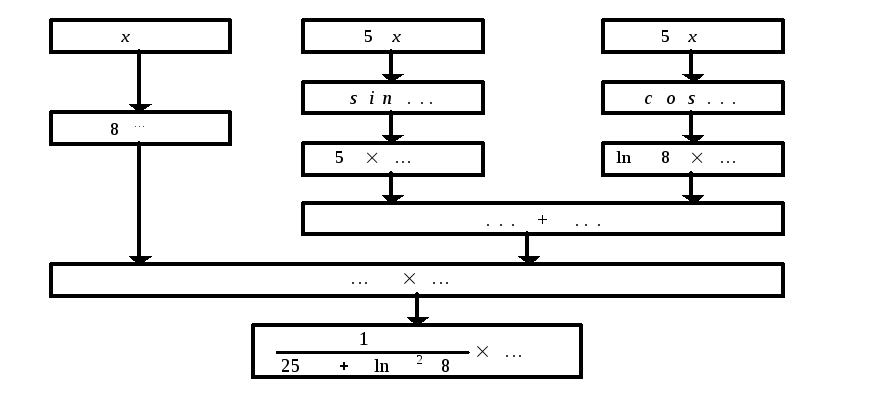
Рис. 9 Схема
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ:
![]()
Дифференциал
Задача 3.
Найдите дифференциал
![]()
Дифференциал
функции находится по формуле:
![]()
Пример.
![]()
Решение:
Найдем производную данной функции
 ;
;
Для нахождения дифференциала данной функции умножаем производную на дифференциал независимой переменной:
![]()
Ответ:
![]() .
.
Задача 4.
Вычислите приближенно с помощью дифференциала.
Если
![]() ,
то
,
то![]() и
и![]()
Примеры:
 Решение:
Решение:
 ;
;

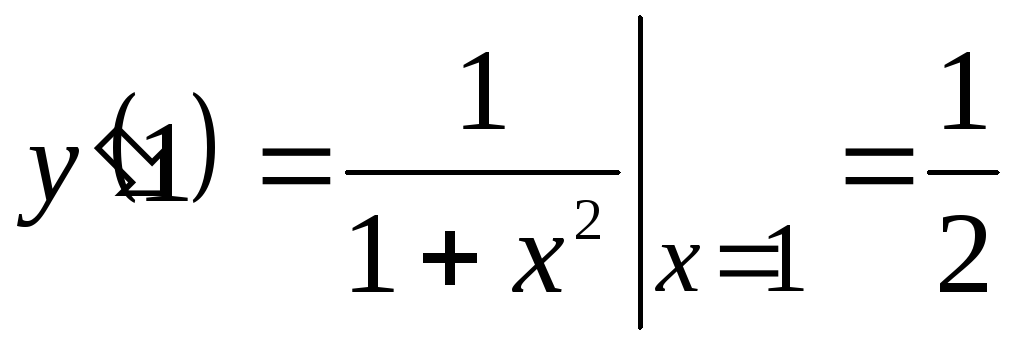
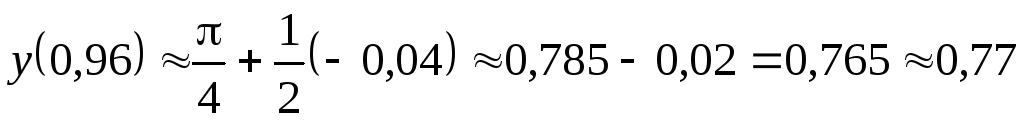 Ответ:
Ответ:
 Решение:
Решение:
 ,
, 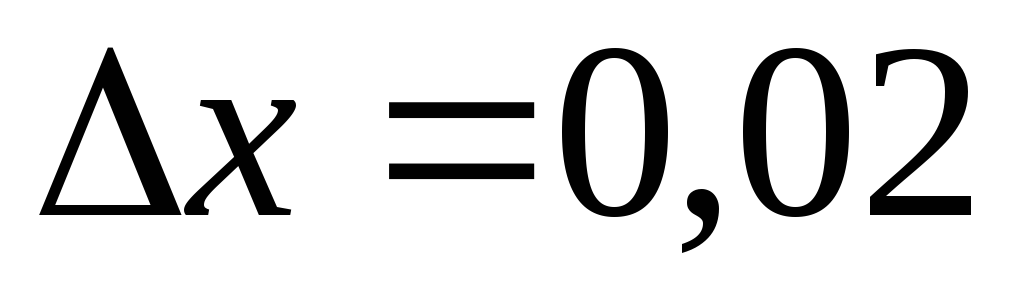
 ,
,

 Ответ:
Ответ:
Производные высших порядков.
Задача 17.
Найдите производную n-го порядка.
Для выполнения этого задания необходимо воспользоваться таблицей производных n-го порядка некоторых функций (смотрите приложение В).
Примеры.
Решение:
![]()
![]()
![]()
![]()
………………………………………
![]()
Ответ:
![]()
Решение:
![]()
Ответ:
![]()
Решение:
![]()
![]()
Ответ:
![]()
Решение:
![]()
![]()
![]()
![]()
…………………………………….
![]()
Ответ:
![]()
Решение:
![]()
![]()
![]()
![]()
………………………………………
![]()
Ответ:
![]()
Решение:
![]()
![]()
………………………………………
![]()
Ответ:
![]()
Решение:
![]()
![]()
![]()
………………………………
![]()
Ответ:
![]()
Решение:
![]()
![]()
![]()
![]()
………………………………
![]()
Ответ:
![]()
Задача 18.
Найдите производную указанного порядка.
Воспользуемся формулой Лейбница
![]()
Пример.
![]()
Решение:
Обозначим
![]() тогда
тогда![]() и можно воспользоваться формулой
Лейбница.
и можно воспользоваться формулой
Лейбница.
|
|
|
|
|
|
|
|
|
|
|
|
Запишем формулу Лейбница для производной 4-го порядка:


![]()
![]()
![]()
Ответ:
![]()
Производные функций, заданных параметрически
Задача 15.
Найдите производную
![]() .
.
Если функция
![]() от независимой переменной
от независимой переменной![]() задана с помощью вспомогательной
переменной (параметра)
задана с помощью вспомогательной
переменной (параметра)![]() :
:

то производная от у по х определяется по формулам:
 (1)
(1)
Примеры.
1.
Решение: Находим
![]() и
и![]() и полученные значения подставляем в
формулу (1)
и полученные значения подставляем в
формулу (1)
 ,
,
 ,
,

Ответ:
![]()
2.![]()
Решение:
Находим
![]() и
и![]() и полученные результаты подставляем
в формулу (1)
и полученные результаты подставляем
в формулу (1)
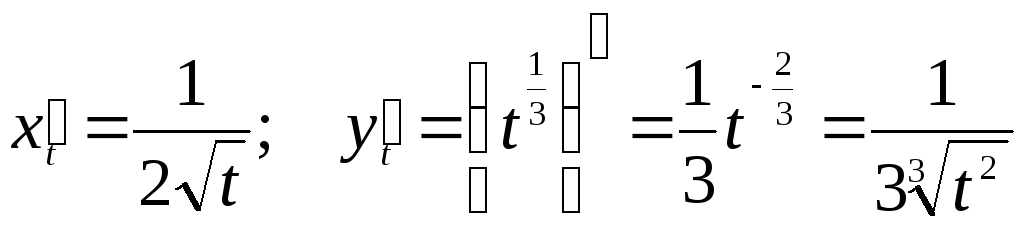

Ответ:
![]()
Задача 19.
Найти производную
второго порядка
![]() от функции заданной параметрически.
от функции заданной параметрически.
Для нахождения второй производной используют следующую формулу
 (2)
(2)
Пример.
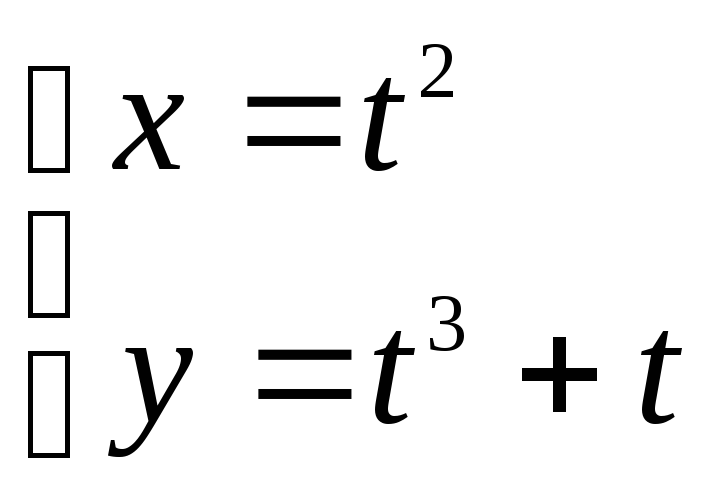
Решение:
Находим производные от x и y по параметру t:
![]()
Искомая производная от y по x находится как отношение производных от y и от x по t:
![]()
Далее находим производную по формуле (2)

![]()
Ответ:
![]()
Уравнения касательной и нормали к кривой в точке
Задача 2.
Составить уравнения
нормали и касательной в точке с абсциссой
![]() .
.
Если кривая
определена уравнением
![]() ,
то уравнение касательной и нормали к
ней в точке М с координатами
,
то уравнение касательной и нормали к
ней в точке М с координатами![]() имеет соответственно вид
имеет соответственно вид
![]() (3)
(3)
![]() (4)
(4)
Этапы выполнения задания:
Подставляя в данное уравнение значение
 ,
находим значение
,
находим значение .
.Находим производную данной функции и ее значение при
 .
.Подставляя значение
 ,
, и
и в уравнение касательной (или нормали),
получим необходимое уравнение.
в уравнение касательной (или нормали),
получим необходимое уравнение.
Пример.
![]() ,
x0
= –1.
,
x0
= –1.
Решение:
Подставляя значение
 в
данное уравнение, находим значение
ординаты
в
данное уравнение, находим значение
ординаты :
:
Находим производную данной функции
 ,
а затем ее значение при
,
а затем ее значение при

Подставляем значения
 ,
, ,
, в уравнения (3) и (4) соответственно,
получаем:
в уравнения (3) и (4) соответственно,
получаем:
![]() - уравнение
касательной
- уравнение
касательной
![]()
![]()
![]() -
уравнение нормали.
-
уравнение нормали.
Ответ:
![]() - уравнение касательной
- уравнение касательной
![]() -
уравнение нормали.
-
уравнение нормали.
