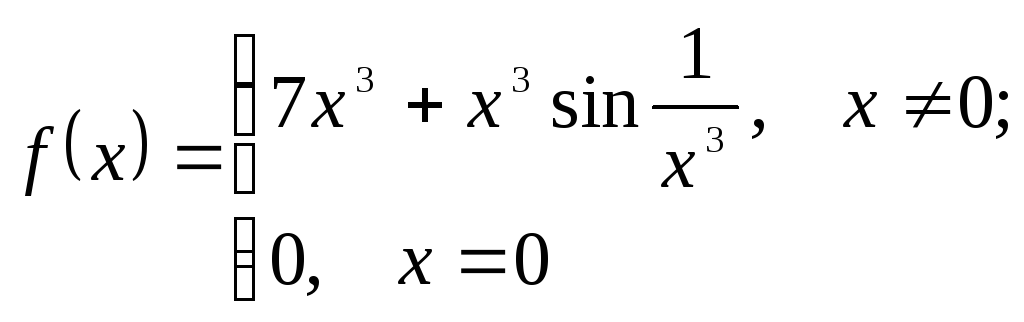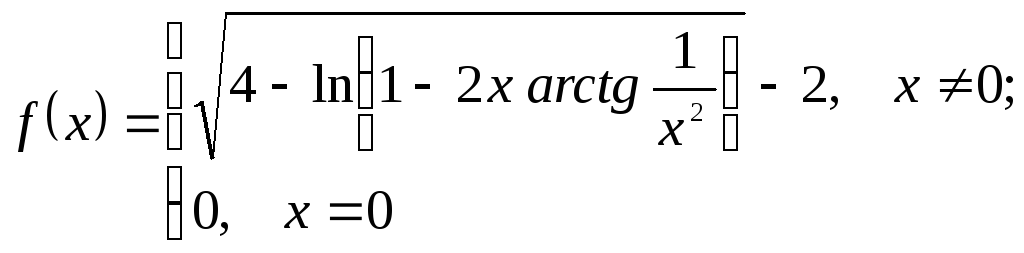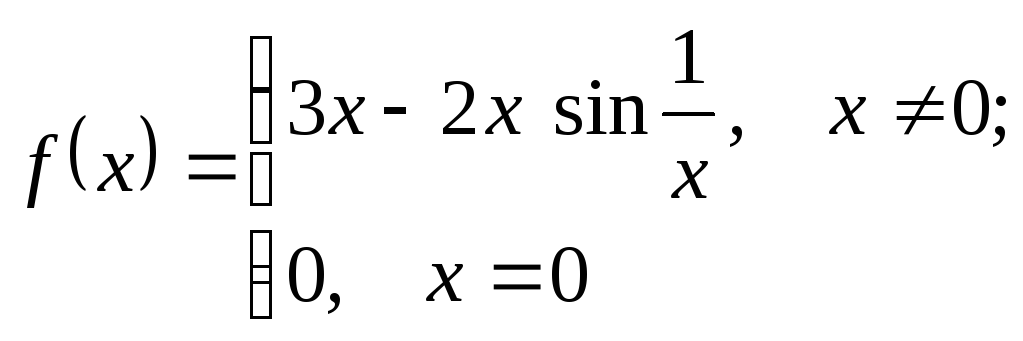Примеры расчетных задач
Производная функции по определению
Задача 1.
Исходя из определения
производной, найдите
.
По определению
производной
.
С учетом того, что
и
,
получим:
Примеры.
Исходя из определения производной,
найдите
Решение:
,
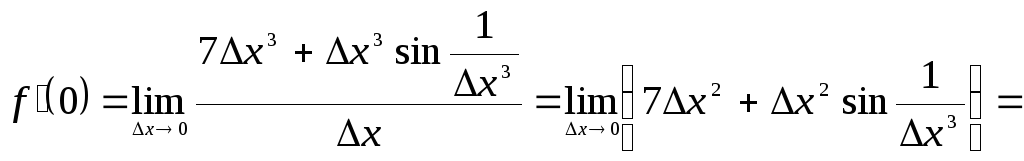
а
-
функция ограниченная, т.е.
значит функция
также
ограничена.
– произведение бесконечно малой функции
на ограниченную функцию. По свойствам
бесконечно малых функций, произведение
бесконечно малой функции на ограниченную
– есть функция бесконечно малая] = 0.
Ответ:
.
Решение:
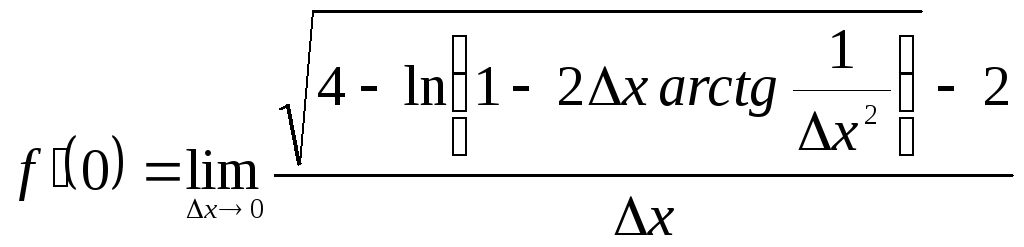(1)
Так как
,
то
.
Непосредственной подстановкой в правую
часть равенства (1)
,
получим неопределенность вида
.
Умножая числитель
и знаменатель на выражение, сопряженное
числителю, т.е. на
,
которое при
стремится к 4, получим
=
,
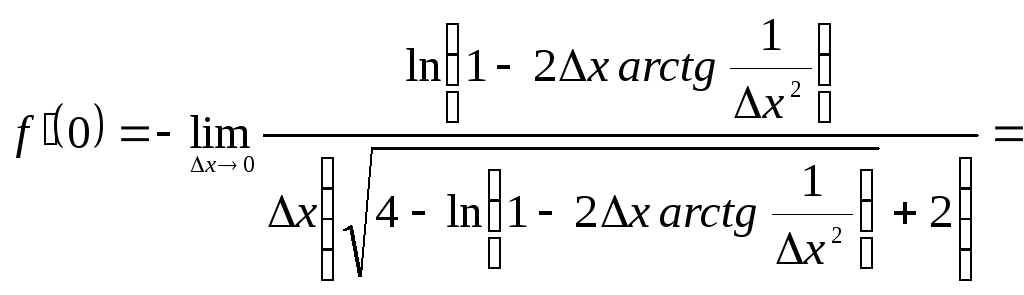
то,
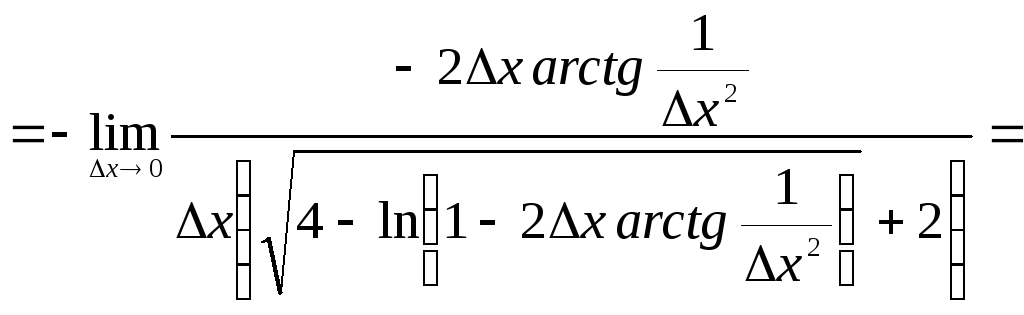
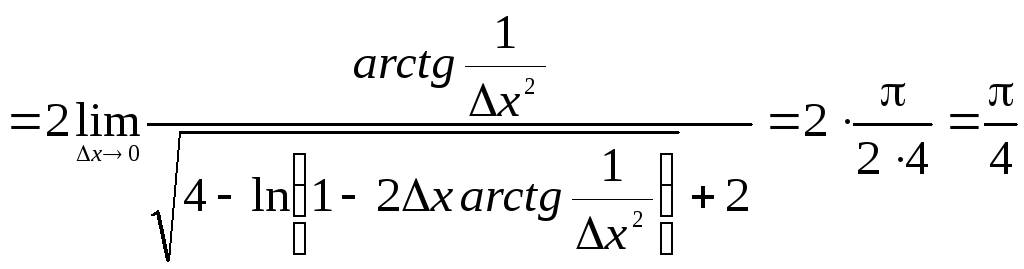
Ответ:
.
Решение:
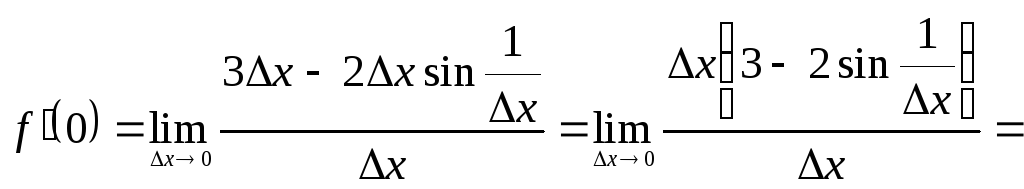
Так как
,
то
- функция ограниченная, но при
она не имеет предела.
Ответ:
не существует.
Производные различных функций
Задача 5.
Найдите производную.
В данном случае
функция представляет собой произведение
(частное) степенных функций. Если
прологарифмировать такое выражение,
получим сумму (разность) логарифмов
сложных функций. Поэтому в этом задании
более рационально находить производную
по формуле
,
а также использовать таблицу производных
степенных функций (Приложение А).
Пример.
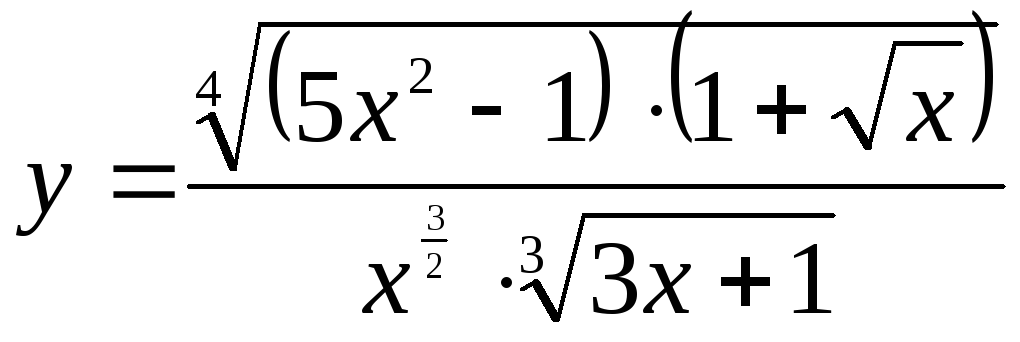
Решение:
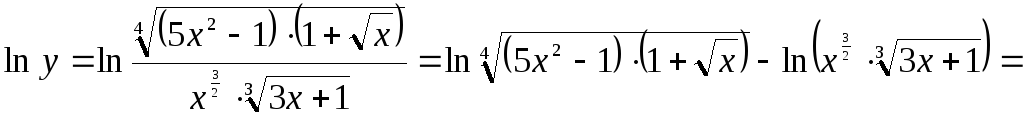
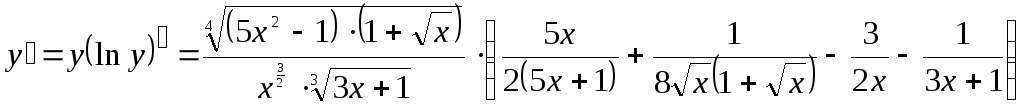
Ответ:
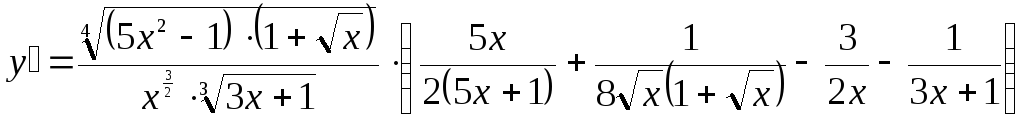
Задача 6.
Найдите производную.
В данном случае необходимо найти производную выражения, включающего в себя показательную функцию (смотрите приложение А).
Пример.
Решение: Составим
схему структуры данной функции (рис.
2).
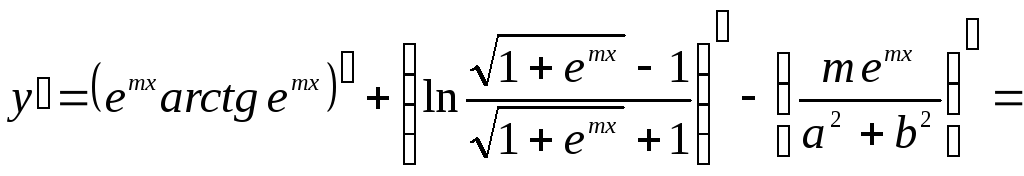
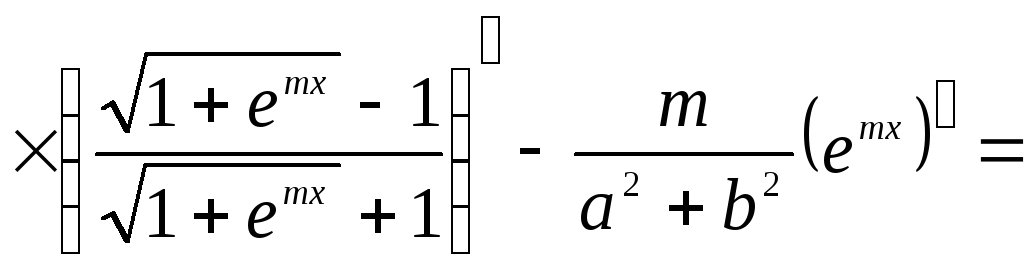
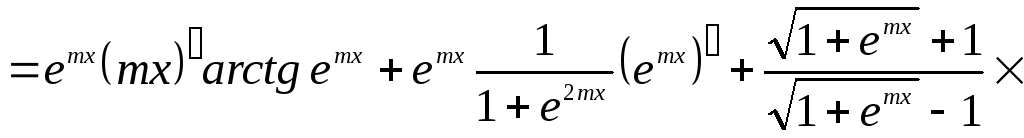
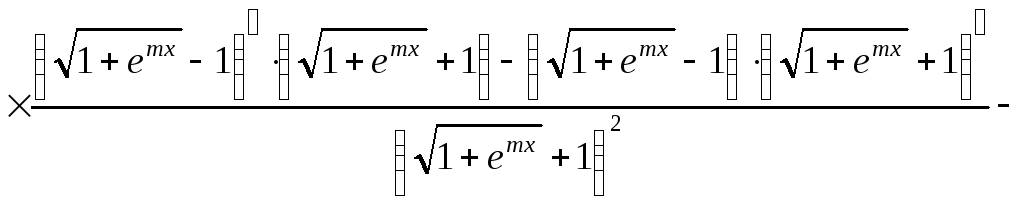
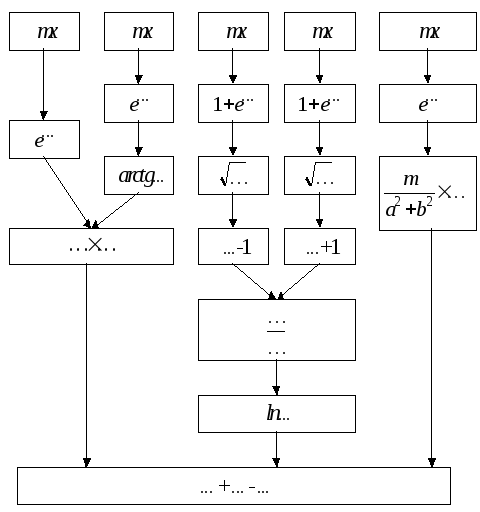
Рис. 2 Схема
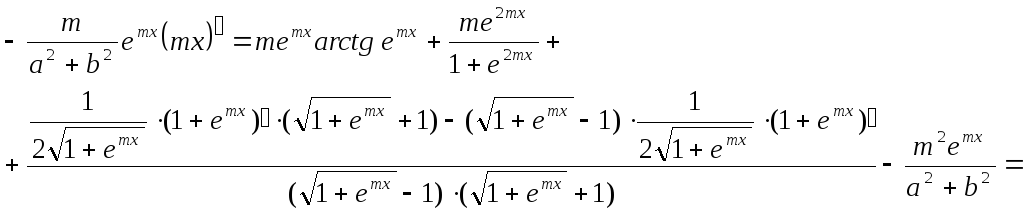
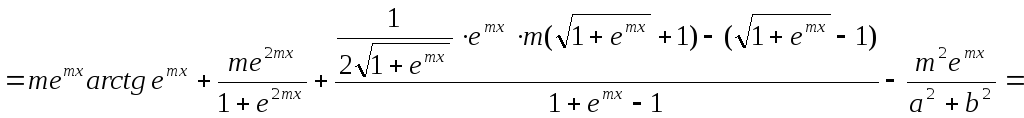
Ответ:
Задача 7.
Найдите производную.
В данном случае необходимо найти производную выражения, включающего в себя логарифмическую функцию (смотрите приложение А).
Пример.
Решение:
Составим схему структуры данной функции (рис. 3)
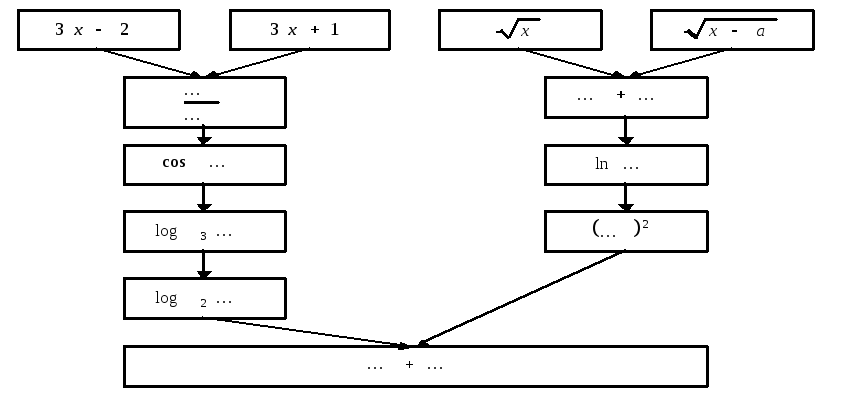
Рис. 3 Схема
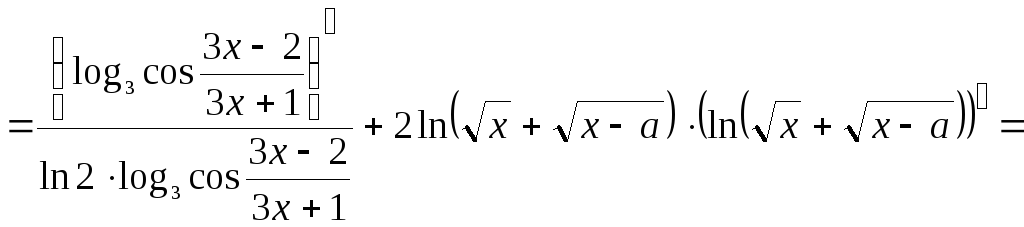
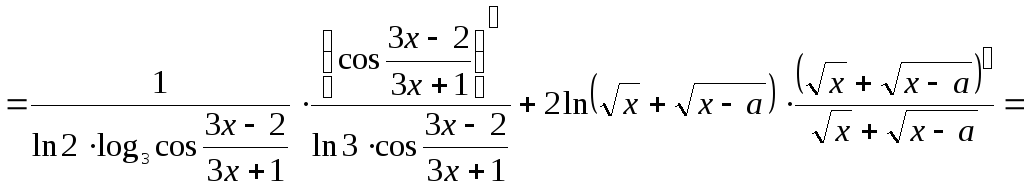
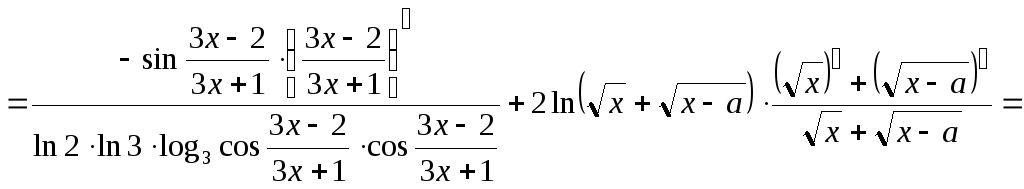
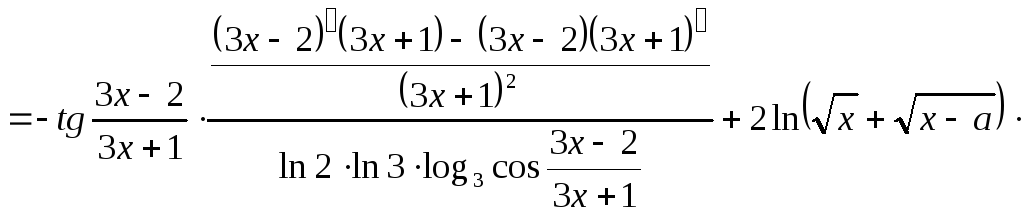
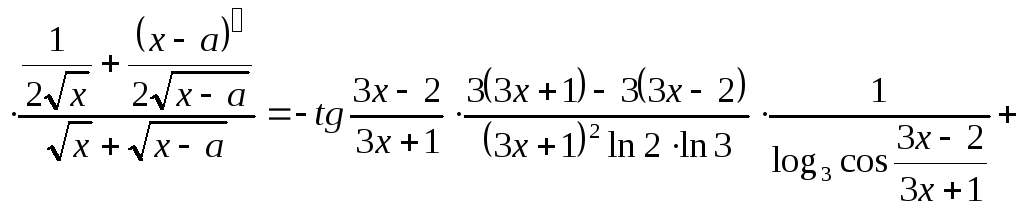
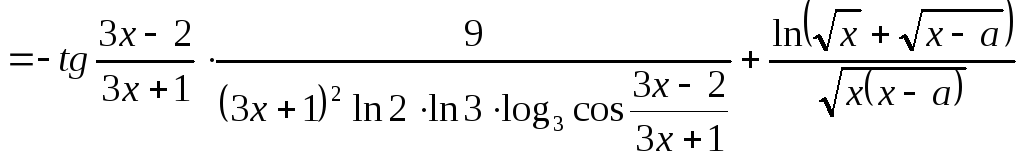
Ответ:
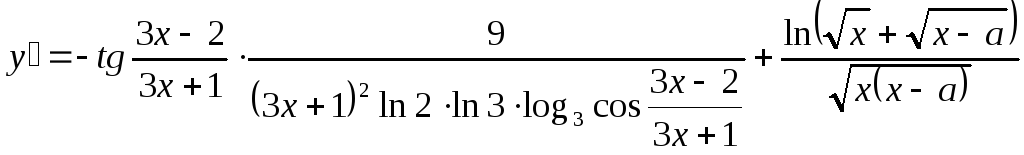
Задача 8.
Найдите производную.
В этом задании, прежде, чем находить производную функции, можно упростить ее, используя тригонометрические формулы:
а
затем производная ищется, опираясь на
производные тригонометрических функций
(смотрите приложение А), с условием
того, что выражения, не содержащие
переменной x,
есть константы
Пример.
Решение:
Ответ:
Задача 9.
Найдите производную.
В данном случае необходимо найти производную выражения, содержащего обратные тригонометрические функции.
Пример.
Решение: Преобразуем данную функцию
Составим схему структуры данной функции (рис. 4)
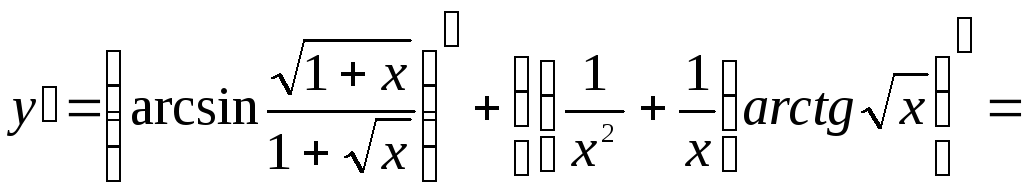
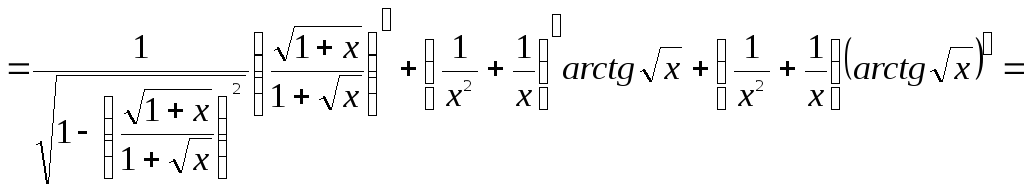
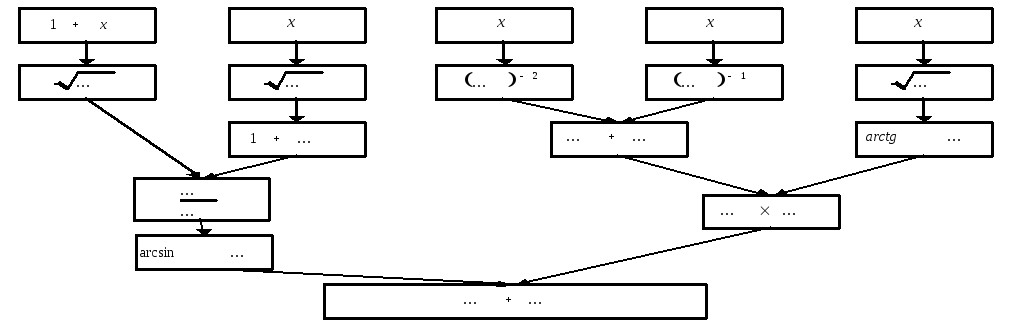
Рис. 4 Схема
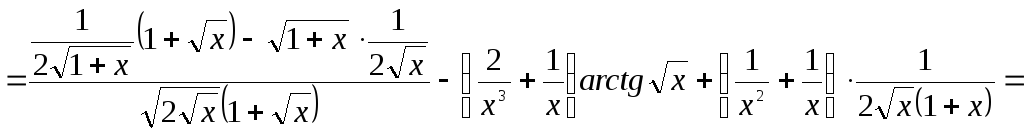
Ответ:
Задача 10.
Найдите производную
В этом задании необходимо найти производную выражения, содержащего гиперболические функции (смотри приложение 1).
Пример.
.
Решение. Преобразуем данную функцию:
Составим схему структуры заданной функции (рис. 5)
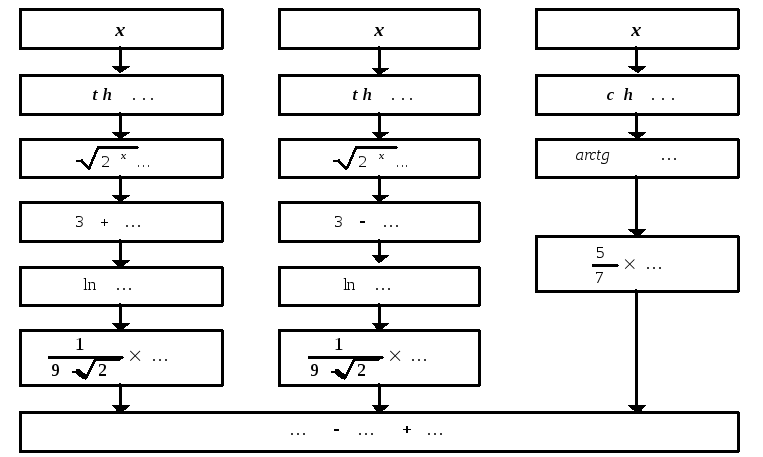
Рис. 5 Схема
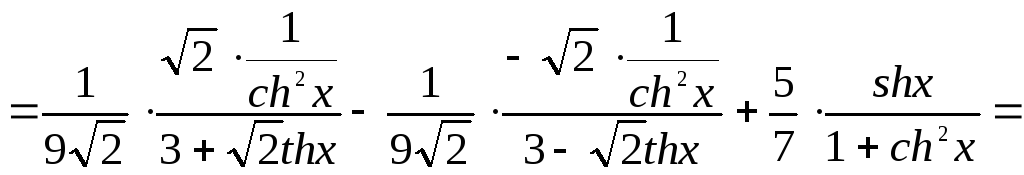
Ответ:
Задача 11.
Найдите производную.
В этом задании
нужно найти производную показательно-степенной
функции вида
.
Для этого воспользуемся формулой:
Таким образом, нахождение производной показательно-степенной функции сводится к вычислению производной произведения.
Пример.
Решение:
Составим схему структуры полученного выражения
Рис. 6 Схема
Ответ:
В задачах 12 – 14, используя приложение А и правила дифференцирования, необходимо найти производные сложных функций.