MU_Predely

Методические указания к выполнению типового расчета по теме « Пределы»

Настоящие «Методические указания» предназначены для студентов I курса всех специальностей дневного и вечернего отделения, выполняющих в первом семестре типовой расчет по теме «Пределы».

«Указания» содержат подробные разъяснения по каждому заданию, методы решения всех типов примеров, входящих в ТР, ссылки на литературу по данному вопросу.

Данное пособие поможет студентам приобрести навыки решения основных задач по теме «Пределы».

Примеры выполнения расчетных заданий.

Задача 1. Доказать, что , указать

; а=2.

Решение: по определению предела последовательности:

2=, если для такой, что для выполняется неравенство: . (1)

Решая это неравенство, находим:

,

,

для n >1: , следовательно, 0< , , ,

Таким образом, неравенство (1) будет выполняться при всех n >, т. е. для такой, что для будет выполняться неравенство (1). За можно взять целую часть числа : =Е().

Например:, ,

, .

Ответ: если для такой, что для выполняется неравенство: , значит =2.

Литература: , стр. 32; , стр. 49 (пр. 2-5); , № 634, 635.

Задача 2 .Вычислить предел числовой последовательности: .

Решение: при непосредственной подстановке предела аргумента получим неопределенность вида .

Упростим числитель и знаменатель дроби:

;

=;

Тогда : .=;

Разделив числитель и знаменатель дроби на старшую степень n ( в данном случае на ), получим: : =.

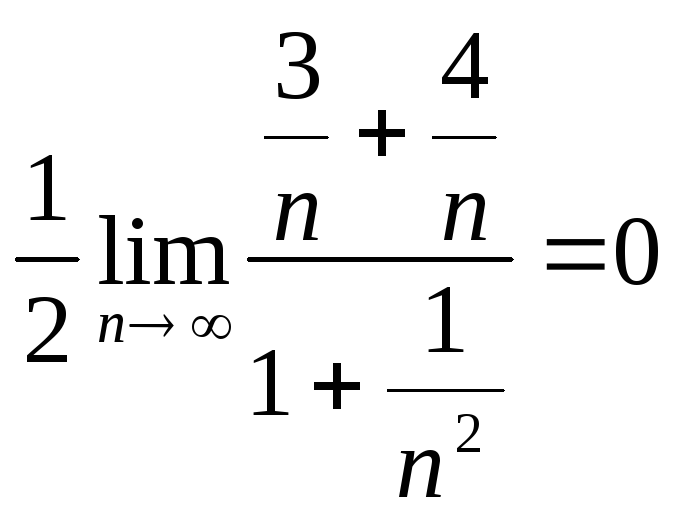
Ответ: =0.

Литература:

Задача 3. Вычислить предел числовой последовательности: .

Решение: при непосредственной подстановке предельного значения аргумента получаем неопределенность . Разделим числитель и знаменатель дроби на старшую степень n (в данном случае на ):

=.

Ответ: =1.

Литература:

Задача 4. Вычислить предел числовой последовательности:.

Решение: в этом примере имеет место неопределенность вида .

Преобразуем выражение, стоящее под знаком предела, умножив и разделив его на выражение, сопряженное выражению, заключенному в скобках:

=.

Тогда: =.

Разделим числитель и знаменатель выражения, стоящего под знаком предела, на старшую степень n ( в данном случае на ):

=.

Ответ: :=0.

Литература:

Задача 5. Вычислить предел числовой последовательности:

а) .

Решение: при непосредственной подстановке предельного значения аргумента получаем неопределенность вида.

Рассмотрим числитель дроби:2+4+6+…+2n = S_n – сумма n членов арифметической прогрессии ( ), т.к. имеем.

Тогда: =, т.к. если числитель и знаменатель дроби имеют равные старшие степени, то предел равен отношению коэффициентов при старших степенях n.

Ответ: =1.

б) .

Решение: при непосредственной подстановке предельного значения аргумента имеем неопределенность .

Вспомним, что

,

Тогда: ==, т. к. степень числителя больше степени знаменателя.

Ответ: =.

в).

Решение: при непосредственной подстановке предельного значения аргумента имеем неопределенность .Разделим числитель и знаменатель дроби на степень с большим основанием:

=, т.к. .

Ответ: =.

Литература: , № 39, 71 (1-4).

Задача 6. Вычислить предел числовой последовательности: .

Решение: здесь имеет место неопределенность вида . Преобразуем последовательность так, чтобы использовать следствие второго замечательного предела:, где-функция целочисленного аргумента:

=

== (применяя теорему о предельном переходе под знаком непрерывной функции) ==

=, т.к. , а .

Ответ: =.

Литература:, стр. 173-174; [9], стр.34; [7], № 648; [8], № 88.

Задача 7. Доказать, что , ( найти ).

Решение: по определению предела функции в точке , если

такое, что, которые подчиняются условию , выполняется неравенство .

Разложим многочлен, стоящий в числителе, на множители: .

Тогда получаем:.

Сократим на ( имеем право выполнить сокращения, т. к. ) и получим:

.

Таким образом мы получили, что из выполнения неравенства следует выполнение неравенства . За можно взять, т.е. .

Ответ: , .

Литература : [1], стр. 78 (пр.1); [3], стр. 35-36 (пр. 1-3), 37-38 (пр. 1-4); [8], № 29.

Задача 8. Доказать, что функция непрерывна в точке . Найти .

Решение: По определению непрерывности функции в точке: функция непрерывна в точке, если, такое, что из выполнения неравенства следует выполнение неравенства .

Зададим и покажем , что можно найти такое , что при любом удовлетворяющем неравенству будет справедливо неравенство.Рассмотрим неравенство:

.

Решим неравенство, считая :

Таким образом, из выполнения неравенства следует выполнение неравенства , а значит функция непрерывна в точке . .

Ответ: функция непрерывна в точке ; .

Литература:

Задача 9. Вычислить предел функции .

Решение: при подстановке предельного значения аргумента получаем неопределенность вида . Так как числитель и знаменатель дроби обращается в ноль при х=1, то х=1 является их корнем. Выделим в числителе и знаменателе множитель (х-1), для чего воспользуемся правилом деления многочлена на двучлен:

-	x3	-	2x2	-	5x	+	6	x-1	-	x3	+	2x2	-	x	-	2	x-1
	x3	-	x2					x2-x-6		x3	-	x2					x2+3x+2
	-	-	x2	-	5x	+	6				-	3x2	-	x	-	2
		-	x2	+	x							3x2	-	3x
			-	-	6x	+	6						-	2x	-	2
				-	6x	+	6							2x	-	2
							0									0

Таким образом:

.

Тогда имеем: =.

Ответ: = -1.

Литература: [3], стр. 45 (пр. 4); [4], стр. 137 (пр. 4); [7], № 638-640; [8], № 52, 71(1,2).

Задача 10. Вычислить предел функции: .

Решение: при непосредственной подстановке предельного значения аргумента получаем неопределенность вида . Освободимся от иррациональности в числителе, дополнив его до разности кубов. Для этого умножим числитель и знаменатель дроби на неполный квадрат суммы:.

=

== .

Ответ: =0.

Литература: [4], стр. 93 (пр.2,3), стр. 136 (пр. 3); [7], № 641, 642, 647; [8], № 53.

Задача 11. Вычислить предел функции .

Решение: при непосредственной подстановке предельного значения аргумента получаем неопределенность вида . Вычислим этот предел, используя теорему о замене бесконечно малых функций эквивалентными ( [9], 9(3), стр.36).

Тогда =

=.

Ответ: =1.

Литература: [3], стр. 48 (пр. 1-4), стр. 52 (пр.1-4); [7], № 643, 644, 703; [8], №54, 78 (1,2); [9], § 6.

Задача 12. Вычислить предел функции .

Решение: при непосредственной подстановке предела аргумента получаем неопределенность вида . При решении подобных примеров удобно сделать замену переменной, чтобы воспользоваться эквивалентными равенствами.

= = (умножим числитель и знаменатель дроби на выражение ) ==

=.

Ответ: =8.

Литература: [4], стр. 113 (пр. 8); [8], № 76; [9], § 4.

Задача 13. Вычислить предел функции .

Решение: при непосредственной подстановке предела аргумента получаем неопределенность вида . Сделаем замену переменной, чтобы воспользоваться эквивалентными равенствами.

=

= .

О твет: =.

Литература:

Задача 14. Вычислить предел функции: .

Решение: при непосредственной подстановке предела аргумента получаем неопределенность вида . Преобразуем выражение стоящее под знаком предела, чтобы воспользоваться следствиями из первого и второго замечательных пределов: в числителе прибавим и вычтем единицу, и затем разделим числитель и знаменатель на .

=.

Ответ: =.

Литература:

Задача 15. Вычислить предел функции: .

Решение: при непосредственной подстановке предела аргумента получаем неопределенность вида . Преобразуем выражение стоящее под знаком предела, чтобы можно было воспользоваться эквивалентными равенствами.

=

=.

Ответ: =0.

Литература:

Задача 16. Вычислить предел функции .

Решение: Непосредственное применение теорем о пределах приводит к неопределенности вида . При решении подобных примеров можно использовать логарифмирование.

Пусть =А, тогда

=

==.

.
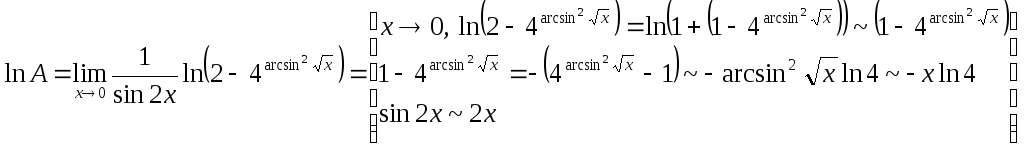