Задачи на нормальное распределение
Задача 39.
Нормальный закон распределения задан в форме уравнения:
.
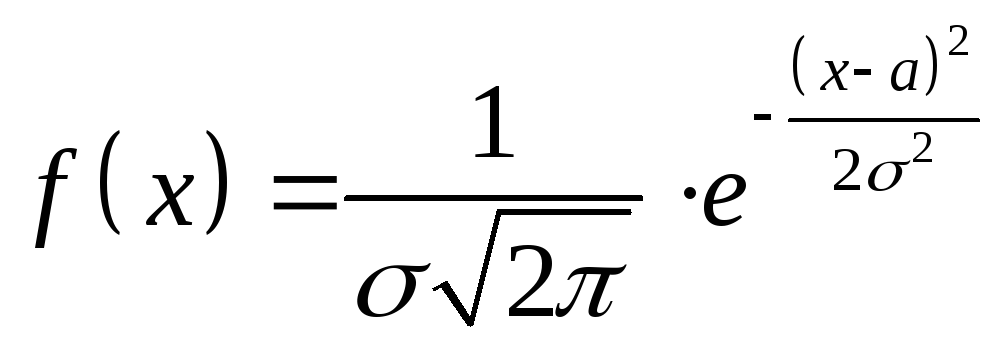Какова вероятность того, что случайная величина примет значения x<a? x>a?
Задача 40.
В нормальном законе распределения a = 2, σ = 4. Чему равно x, если вероятность того, что случайная величина принимает значения меньше x, равна 3/4?
Задача 41.
Проведены точные измерения дозированного медицинского препарата, предназначенного для инъекций и содержащегося в ампулах по 1 мл в каждой ампуле, с целью уточнения влияния количества вводимого препарата на лечебный эффект.
При проверке 12 ампул получили следующие результаты (в мл):
0,97; 1,07; 1,02; 1,04; 0,97; 0,96; 1,03; 1,05; 0,96; 0,97; 1,05; 1,01.
Считая, что распределение подчиняется нормальному закону, определить вероятность того, что в ампуле меньше одного миллилитра раствора.
Задача 42.
Анализ веса 100 новорожденных показал, что у них в интервале от 1,75 до 2,25 (со средним весом 2 кг) попало 5 новорожденных; со средним весом 2,5 кг попало 25 новорожденных, со средним весом 3 кг — 40, 3,5 кг — 25 и 4 кг - 5 новорожденных. Совпадает ли это распределение с нормальным распределением Гаусса? Определить по полученным данным вероятность рождения недоношенного ребенка (m 2.4 кг).
Задачи на распределение Стьюдента
Задача 43.
Измерение веса девочек в возрасте 10 лет дало следующие результаты :
|
Вес (кг) |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
Число лиц |
2 |
1 |
6 |
8 |
21 |
20 |
18 |
12 |
3 |
4 |
2 |
3 |
Найти среднее арифметическое значение веса девочек, стандартное отклонение и ошибку среднего арифметического для PD=0,9.
Задача 44.
Пять измерений относительной вязкости крови человека дали следующие результаты: 4,80; 4,70; 4,85; 4,75; 4,90. Найти среднее значение, стандартное отклонение и ошибку среднего арифметического.
Задача 45.
Определить среднее значение и стандартное отклонение по данным 20 измерений максимального кровяного давления у одного больного за период болезни :
98, 160, 136, 128, 130, 114, 123, 134, 128, 107, 123, 125, 129, 132, 154, 115, 126, 132, 136, 130.
Задачи на обработку прямых и косвенных измерений
Задача 46.
Десять измерений диаметра капилляра в стенке легочных альвеол дали следующие результаты(в мм):
2.83; 2.82; 2.81; 2.85; 2.87; 2.86; 2.83; 2.85; 2.83; 2.84.
Провести обработку серии этих измерений для PD=0,95.
Задача 47.
Проведены измерения спектральной чувствительности уха на пороге слышимости. Уровень слышимости (L, дБ) измерялся на каждой частоте три раза. Получены следующие результаты:
|
Частота |
L1 |
L2 |
L3 |
|
50 |
-12 |
-13 |
-10 |
|
100 |
-12 |
-15 |
-15 |
|
500 |
-20 |
-25 |
-20 |
|
800 |
-40 |
-44 |
-46 |
|
1000 |
-60 |
-70 |
-68 |
|
3000 |
-54 |
-58 |
-58 |
|
8000 |
-39 |
-48 |
-45 |
|
10000 |
-30 |
-35 |
-33 |
|
15000 |
-10 |
-12 |
-8 |
Провести обработку результатов измерений для PD=0,9.
Построить график зависимости уровня интенсивности от частоты с указанием доверительных интервалов.
Задача 48.
Провести обработку результатов измерений лабораторной работы «Изучение аппарата УВЧ»
По классу точности миллиамперметра вычислить систематическую ошибку для измерения силы тока (см. задание 1).
Ошибку в измерении температуры принять равной половине цены наименьшего деления термометра (см. задание 2).
По результатам построить график с указанием доверительных интервалов.