23.ПОСТРОЕНИЕ ДВУМЕРНЫХ ГРАФИКОВ В MATHCAD

23.4.Создание трехмерных графиков

•трехмерный график рассеяния;

•трехмерный график векторного поля.

В зависимости от типа графика, процедура его создания имеет свои особенности. Сначала рассмотрим, как создаются графические поверхности.

23.4.1. Создание поверхностей

График-поверхность создается для функций, зависящих от двух аргументов. При этом по горизонтальным осям обычно отображаются значения независимых переменных, а вдоль вертикальной оси отсчитывают значение зависимой переменной, т. е. функции. Эта функция может быть задана как в явном виде, так и в параметрическом. Кроме того, можно создавать поверхности по массивам данных, что с практической точки зрения весьма важно и удобно (рис. 23.13).

Рис. 23.13

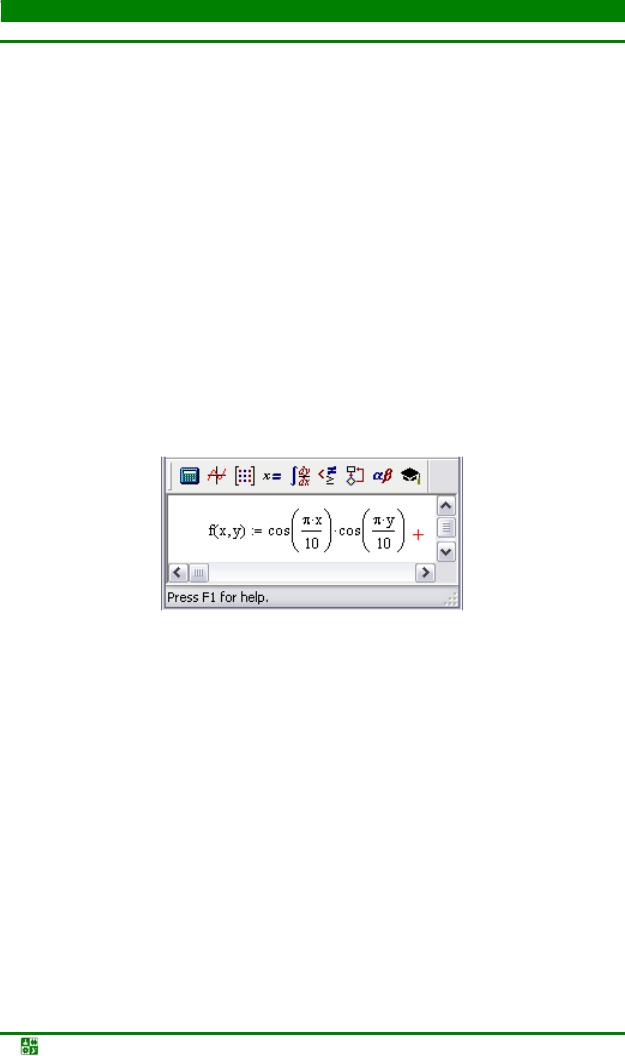
Простой и быстрый способ построения графика-поверхности подразумевает на первом этапе определение функции двух переменных.

Далее следует выбрать команду Insert | Graph | Surface Plot (или нажать комбинацию клавиш <Ctrl>+<2>). В результате в рабочую область документа будет вставлена область трехмерного графика-поверхности, содержащая три перпендикулярные координатные оси и структурный заполнитель в левом нижнем углу – см. рис. 23.14.

23.ПОСТРОЕНИЕ ДВУМЕРНЫХ ГРАФИКОВ В MATHCAD

23.4.Создание трехмерных графиков

Рис. 23.14

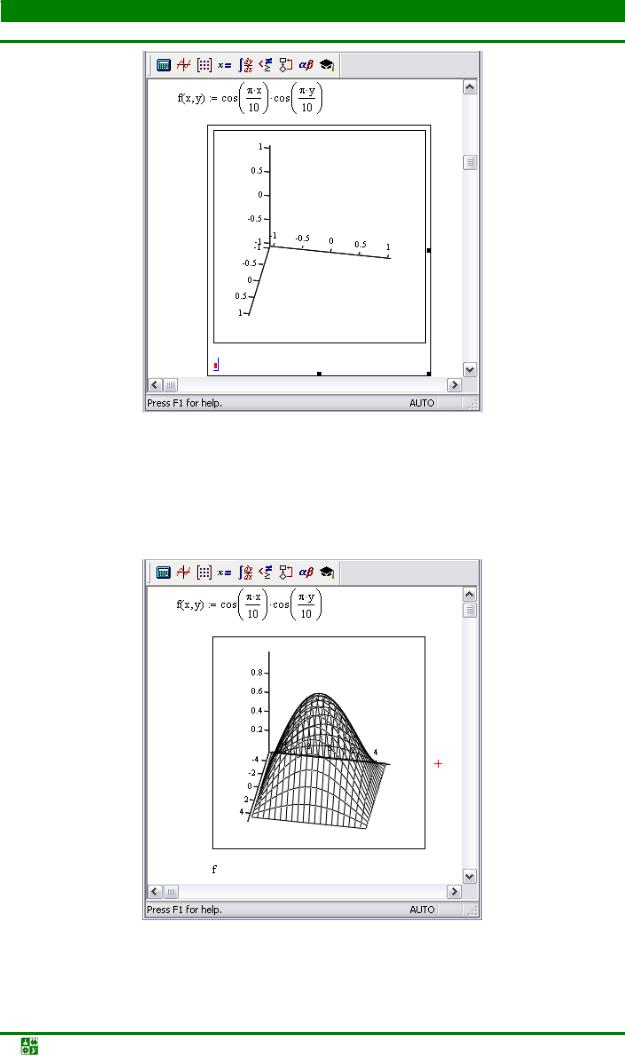
Вместо структурного заполнителя следует ввести название (без аргументов!) функции, определенной ранее. После щелчка мышью вне области графика, системой создается соответствующая поверхность – см. рис. 23.15.

Рис. 23.15

Несложно заметить, что область изменения аргументов для отображае-

23.ПОСТРОЕНИЕ ДВУМЕРНЫХ ГРАФИКОВ В MATHCAD

23.4.Создание трехмерных графиков

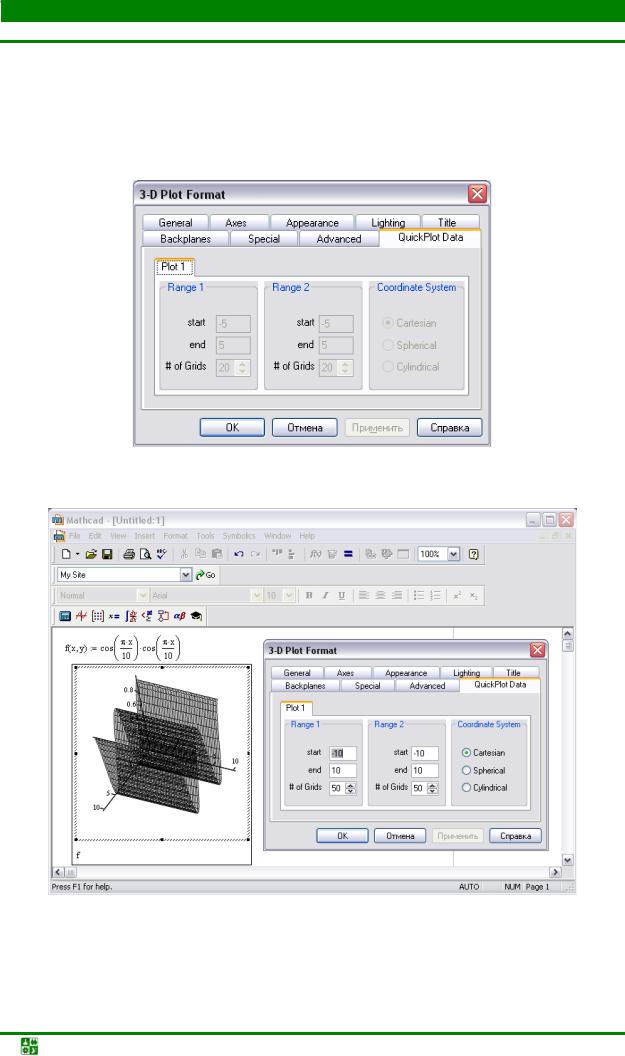
мой функциональной зависимости нигде в явном виде не указывалась. Предлагаемый системой по умолчанию диапазон значений, для которого строится зависимость, можно изменить уже после создания графика. Для этого выполняется двойной щелчок в области графика и в открывшемся диалоговом окне

3-D Plot Format переходят к вкладке QuickPlot Data.

Рис. 23.16

Рис. 23.17

На рис. 23.16 показано, как будет выглядеть созданный ранее график, если его строить в диапазоне изменения переменных от –10 до 10 при 50 узловых точках по каждой из осей.

23.ПОСТРОЕНИЕ ДВУМЕРНЫХ ГРАФИКОВ В MATHCAD

23.4.Создание трехмерных графиков

Вразделе Coordinate System вкладки QuickPlot Data размещена груп-

па переключателей на три позиции, с помощью которой выбирается тип координатной системы: декартова (положение переключателя Cartesian), сферическая (положение Spherical) или цилиндрическая (положение Cylindrical) – см. рис. 23.17. Вкладка QuickPlot Data может сама состоять из

нескольких (для каждой поверхности) вкладок. В рассмотренном примере строилась одна поверхность, поэтому описанные поля и переключатели размещены на единой вкладке.

23.4.2. Основные настройки трехмерного графика

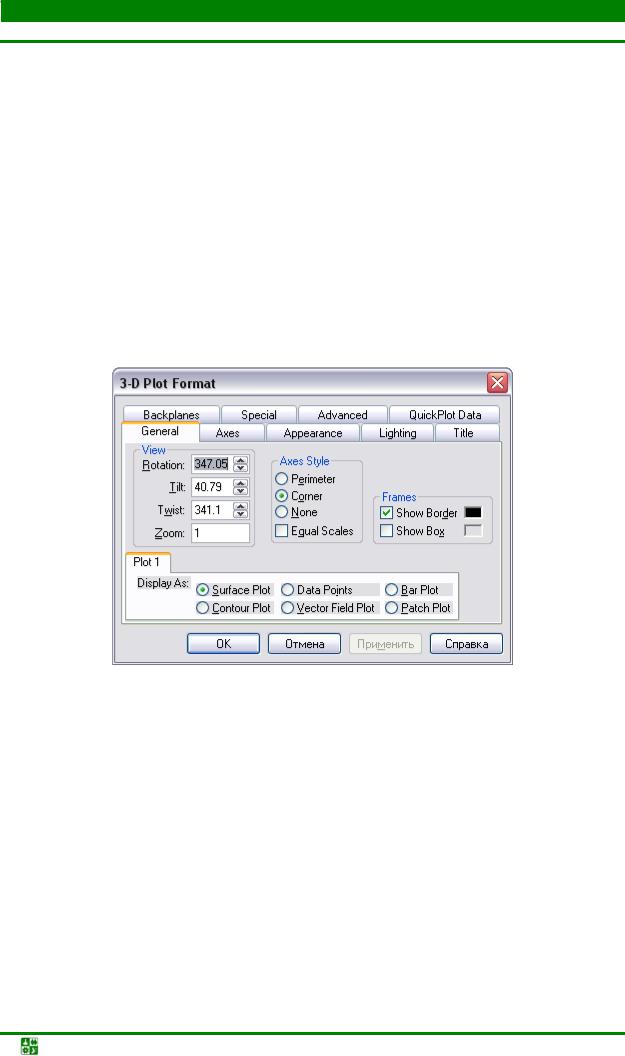
Добиться желаемого вида для трехмерного графика можно, выполнив некоторые настройки на вкладках диалогового окна 3-D Plot Format. Диалоговое окно, открытое на вкладке General, показано на рис. 23.18.

Рис. 23.18

В разделе View на этой вкладке размещены четыре поля: Rotation, Tilt, Twist и Zoom. В трех полях Rotation, Tilt и Twist указываются углы поворотов системы координат при отображении, а в поле Zoom вводится коэффициент масштабирования (он может быть и больше единицы). Ориентация системы определяется, фактически, углами Эйлера. В табл. 23.2 более детально описан способ определения этих углов.

В разделе Axes Style задается способ отображения координатных осей. Раздел состоит из переключателя на три положения и опции Equal Scales. Флажок опции устанавливается в том случае, если нужно, чтобы масштаб вдоль всех координатных осей был единым. Установив переключатель в положение: Perimeter, можно перейти в режим, при котором координатные оси отображаются на переднем плане в области рисунка. По умолчанию переключатель установлен в положение Corner. В этом случае координатные оси

23.ПОСТРОЕНИЕ ДВУМЕРНЫХ ГРАФИКОВ В MATHCAD

23.4.Создание трехмерных графиков

пересекаются в углу, в начале системы координат. Чтобы не отображать координатные оси совсем, переключатель устанавливают в положение None.

Раздел Frames содержит всего две опции: Show Border и Show Box. Hаличие флажка опции приводит к отображению границы области рисунка при его выделении и рамок ограничивающего рисунок параллелепипеда соответственно. Справа от опций расположены поля выбора цвета. При активной опции щелчок на этом поле приводит к открытию специального диалогового окна, в котором выбирается необходимый цвет.

Вкладка в нижней части диалогового окна 3-D Plot Format, открытого на вкладке General, содержит группу переключателей Display As. Переклключатель может находиться в одном из шести положений, и в каждом случае будет задаваться определенный тип графика.

24.ЗАДАНИЕ СОБСТВЕННЫХ ФУНКЦИЙ

ИПРОГРАММИРОВАНИЕ В MATHCAD

24.1. СобственныефункциивMathCad

Практические возможности любого математического приложения определяются во многом тем набором встроенных функций, которые доступны пользователю в работе. Не является исключением и MathCad. Сразу оговоримся, что в MathCad встроенных функций достаточно много. Практически все они математические. Кроме этого, на основе встроенных функций пользователь может определять собственные. Делается это достаточно просто (так же просто, как и большинство других операций в MathCad).

В частности, для того, чтобы определить в рабочем документе функцию пользователя, необходимо ввести ее название, в скобках после названия указать аргумент. Если аргументов несколько, разделяют запятыми. После этого вводится оператор присваивания и выражение, которым непосредственно и задается функция. В этом выражении должны присутствовать аргументы функции, а также могут быть другие переменные, которые следует предварительно инициализировать. В противном случае переменные выделяются цветом, а в рабочем документе появляется сообщение соответствующего характера. Чтобы узнать значение функции для какого-то конкретного аргумента, функцию вызывают с этим аргументом и после нее указывают знак равенства.

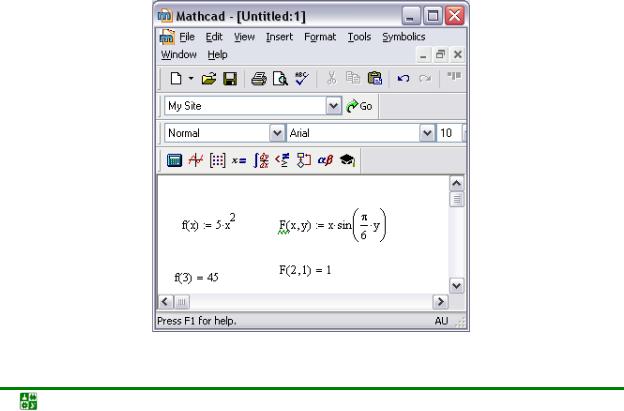
Пример определения простых функций пользователя с одним и двумя аргументами приведен на рис. 24.1. Там же представлены команды, с помощью которых вычисляются значения функций для конкретных численных значений аргументов.

Рис. 24.1

24.ЗАДАНИЕ СОБСТВЕННЫХ ФУНКЦИЙ И ПРОГРАММИРОВАНИЕ В MATHCAD

24.1.Собственные функции в MathCad

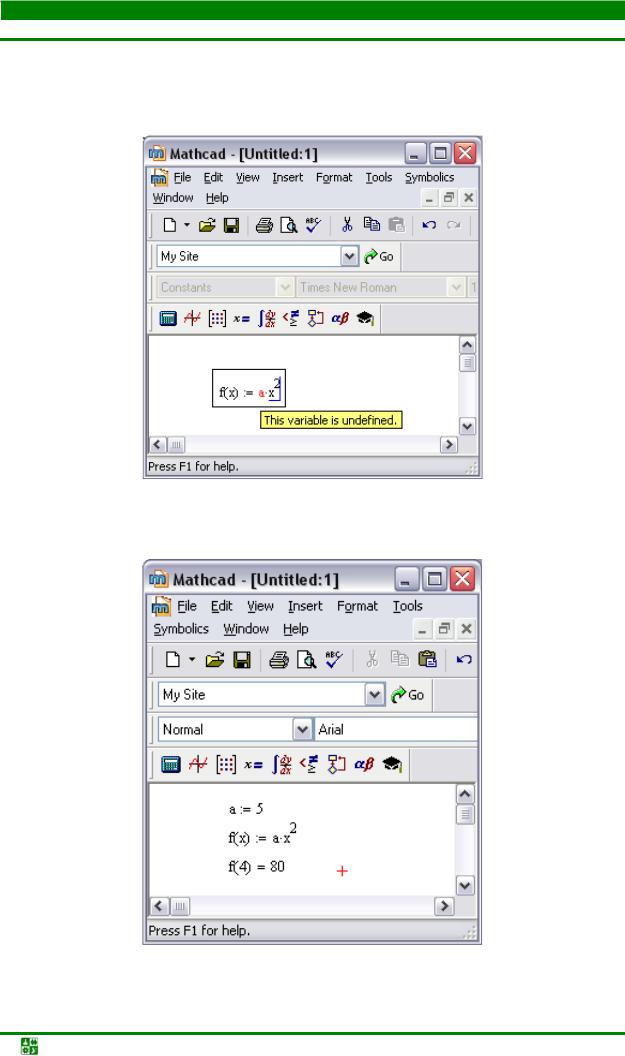
Ситуация, когда в определении функции пользователя встречается переменная, значение которой не определено показана на рис. 24.2. В этом случае, как уже отмечалось, появляется соответствующее сообщение.

Рис. 24.2

Рис. 24.3

24.ЗАДАНИЕ СОБСТВЕННЫХ ФУНКЦИЙ И ПРОГРАММИРОВАНИЕ В MATHCAD

24.1.Собственные функции в MathCad

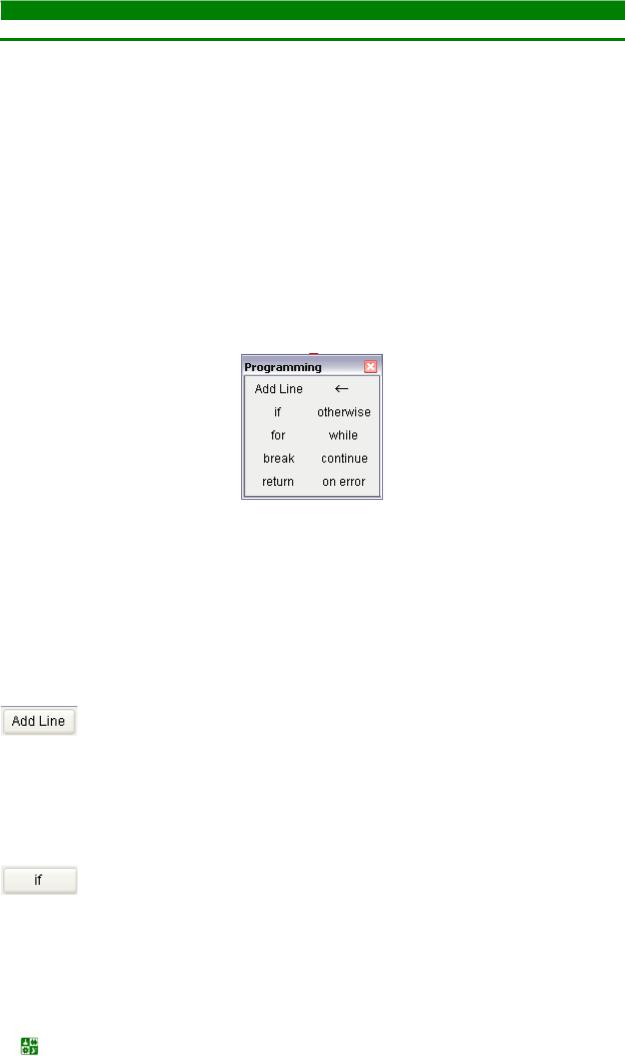
Выйти из ситуации несложно. Для этого перед определением функции нужно ввести команду присваивания значения переменной – см. рис. 24.3.

24.2. ОсновыпрограммированиявMathcad

Программой, как известно, называется упорядоченная последовательность инструкций, объединенных в единую логическую структуру. Программа обычно подразумевает более чем одну последовательность действий и этим отличается от формального набора команд. В каждой программной среде есть свои правила записи инструкций, которые образуют язык программирования. Для создания программ в MathСad предусмотрены специальные утилиты, а для ввода в рабочем документе структур, посредством которых записываются программы, имеется специальная палитра.

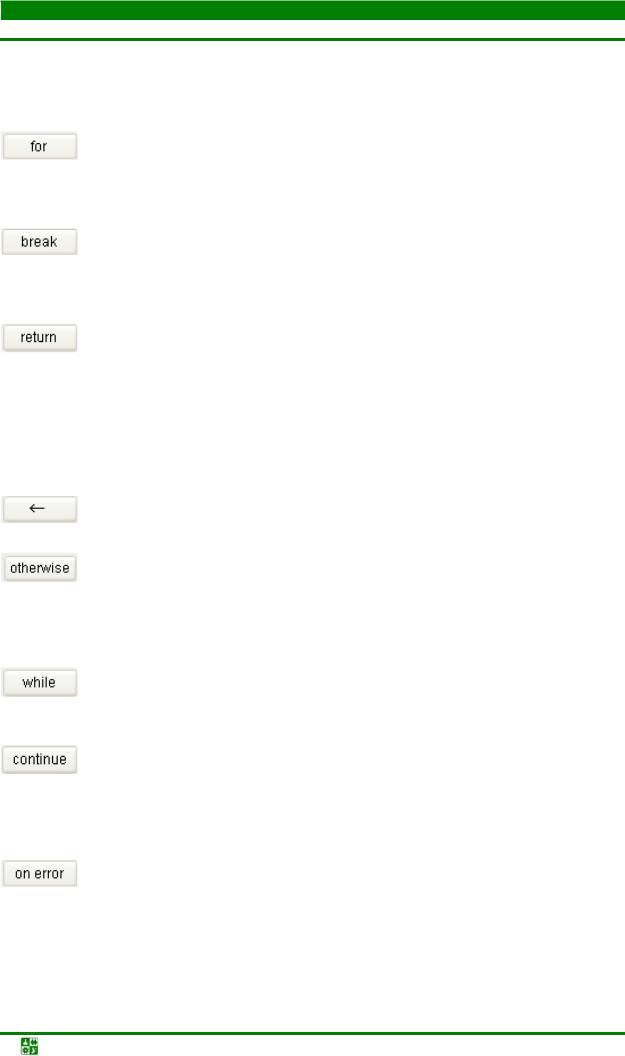
Рис. 24.4

На палитре Programming представлено десять пиктограмм для ввода различных инструкций – см. рис. 24.4. Кратко каждая пиктограмма описана в табл. 24.1.

24.ЗАДАНИЕ СОБСТВЕННЫХ ФУНКЦИЙ И ПРОГРАММИРОВАНИЕ В MATHCAD

24.2.Основы программирования в Mathcad

Окончание табл. 24.1

24.ЗАДАНИЕ СОБСТВЕННЫХ ФУНКЦИЙ И ПРОГРАММИРОВАНИЕ В MATHCAD

24.2.Основы программирования в Mathcad

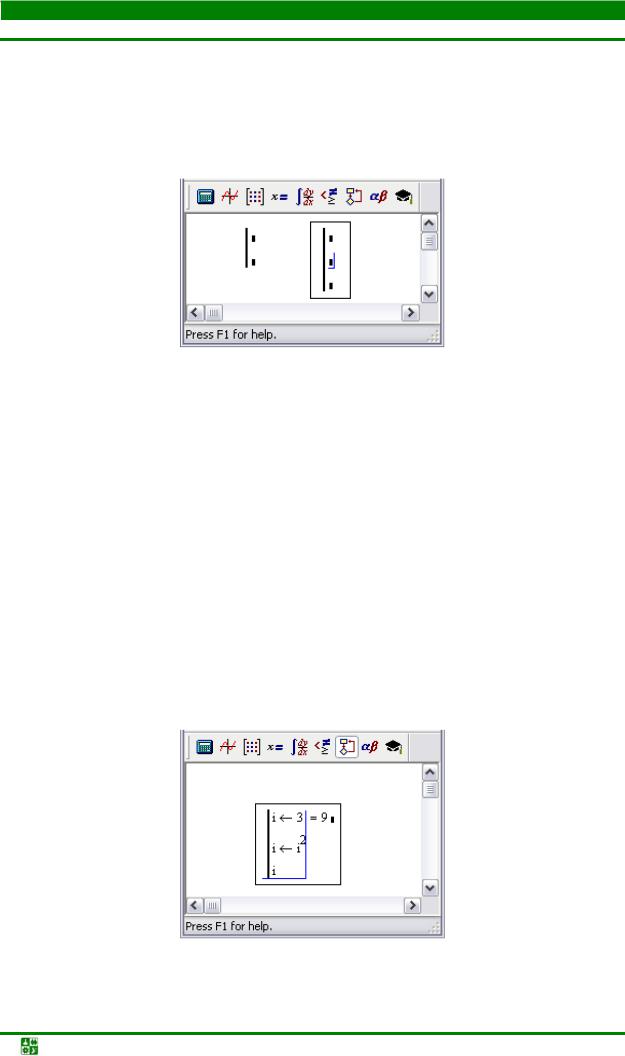
Каждая программа в рабочем документе MathCad реализуется в виде отдельного блока или модуля. Структура этого блока вставляется в рабочий документ щелчком на пиктограмме Add Line на палитре Programming или нажатием клавиши <]>.

Рис. 24.5

Вместо структурных заполнителей вводятся инструкции (команды) программы, которые должны быть выполнены. Для того чтобы добавить еще один структурный заполнитель (чтобы потом вместо него можно было ввести очередную команду), необходимо снова щелкнуть на пиктограмме Add Line.

Для удаления лишнего структурного заполнителя достаточно выделить его и нажать клавишу <Delete>. Обычно программой возвращается значение (хотя и не обязательно). Этот результат к концу выполнения программы, как правило, записан в качестве значения некоторой переменной, указываемой в последней команде программы (рис. 24.5). Следует также иметь в виду, что в теле программы используется оператор локального присваивания, который имеет вид левонаправленной стрелки и вводится с помощью панели инструментов Programming или нажатием комбинации клавиш <Shift>+<[>.

Например, возведем число 3 в квадрат.

Рис. 24.6