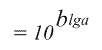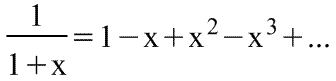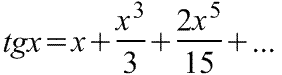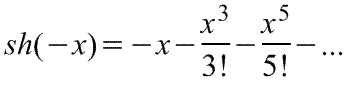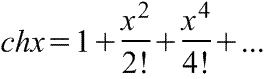Таблица первообразных / Таблица первообразных
.docxТаблица первообразных ("интегралов"). Таблица интегралов. Табличные неопределенные интегралы. (Простейшие интегралы и интегралы с параметром). Формулы интегрирования по частям. Формула Ньютона-Лейбница.
|
Таблица первообразных ("интегралов"). Табличные неопределенные интегралы. (Простейшие интегралы и интегралы с параметром). |
|
|
Интеграл степенной функции. |
Интеграл степенной функции. |
|
Интеграл, сводящийся к интегралу степенной функции, если загнать х под знак диффференциала. |
|
|
|
|
|
Интеграл экспоненциальной функции. |
Интеграл экспоненты, где a-постоянное число. |
|
Интеграл сложной экспоненциальной функции. |
Интеграл экспоненциальной функции. |
|
|
|
|
Интеграл, равняющийся натуральному логорифму. |
Интеграл : "Длинный логарифм". |
|
|
Интеграл : "Длинный логарифм". |
|
Интеграл : "Высокий логарифм". |
Интеграл, где х в числителе заводится под знак дифференциала (константу под знаком можно как прибавлять, так и отнимать), в итоге схож с интегралом, равным натуральному логорифму. |
|
Интеграл : "Высокий логарифм". |
|
|
|
|
|
Интеграл косинуса. |
Интеграл синуса. |
|
Интеграл, равный тангенсу. |
Интеграл, равный котангенсу. |
|
|
|
|
Интеграл, равный как арксинусу, так и арккосинусу |
Интеграл, равный как арктангенсу, так и арккотангенсу. |
|
Интеграл, равный как арксинусу, так и арккосинусу. |
Интеграл, равный как арктангенсу, так и арккотангенсу. |
|
|
|
|
Интеграл равный косекансу. |
Интеграл, равный секансу. |
|
Интеграл, равный арксекансу. |
Интеграл, равный арккосекансу. |
|
Интеграл, равный арксекансу. |
Интеграл, равный арксекансу. |
|
|
|
|
Интеграл, равный гиперболическому синусу. |
Интеграл, равный гиперболическому косинусу. |
|
Интеграл, равный гиперболическому тангенсу. |
Интеграл, равный гиперболическому котангенсу. |
|
Интеграл, равный гиперболическому синусу, где sinhx - гиперболический синус в ангийской версии. |
Интеграл, равный гиперболическому косинусу, где sinhx - гиперболический синус в ангийской версии. |
|
Интеграл, равный гиперболическому тангенсу. |
Интеграл, равный гиперболическому котангенсу. |
|
Интеграл, равный гиперболическому секансу. |
Интеграл, равный гиперболическому косекансу. |
Формулы интегрирования по частям. Правила интегрирования.
|
Формулы интегрирования по частям. Формула Ньютона-Лейбница.Правила интегрирования. |
|
|
Интегрирование произведения (функции) на постоянную: |
|
|
Интегрирование суммы функций: |
|
|
Формула интегрирования по частям неопределенные интегралы: |
|
|
Формула интегрирования по частям определенные интегралы: |
|
|
Формула Ньютона-Лейбница определенные интегралы: |
Где F(a),F(b)-значения первообразных в точках b и a соответственно. |
Таблица производных. Табличные производные. Производная произведения. Производная частного. Производная сложной функции.
Если x - независимая переменная, то:
|
Таблица производных. Табличные производные."таблица производный"-да, к сожалению, именно так их и ищут в интернете |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Производная натурального логарифма функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Правила дифференцирования. Производная произведения. Производная частного. Производная сложной функции. |
|
|
Производная произведения (функции) на постоянную: |
|
|
Производная суммы (функций): |
|
|
Производная произведения (функций): |
|
|
Производная частного (функций): |
|
|
Производная сложной функции: |
|
Свойства логарифмов. Основные формулы логарифмов. Десятичные (lg) и натуральные логарифмы (ln).
|
|
|
|
|
|
|
|
|
|
|
|
|
Основное логарифмическое тождество |
|
|
Покажем как можно любую функцию вида ab сделать экспоненциальной. Поскольку функция вида ех называется экспоненциальной, то |
|
|
Любая функция вида a b может быть представлена в виде степени десяти |
|
Натуральный логарифм ln (логарифм по основанию е = 2,718281828459045… ) ln(e)=1; ln(1)=0
|
При |
|
логарифм числа (1+х) разлагается в ряд: |
|
|
||
|
Например, |
||
|
|
||
|
|
|
|
Ряд Тейлора. Разложение функции в ряд Тейлора.
Оказывается, большинство практически встречающихся математических функций могут быть с любой точностью представлены в окрестностях некоторой точки в виде степенных рядов, содержащих степени переменной в порядке возрастания. Например, в окрестности точки х=1:


При использовании рядов, называемых рядами Тейлора, смешанные функции, содержащие, скажем, алгебраические, тригонометрические и экспоненциальные функции, могут быть выражены в виде чисто алгебраических функций. С помощью рядов зачастую можно быстро осуществить дифференцирование и интегрирование.
Ряд Тейлора в окрестности точки a имеет виды:
1) ,
где f(x) - функция, имеющая при х=а производные
всех порядков. Rn
- остаточный член в ряде Тейлора
определяется выражением
,
где f(x) - функция, имеющая при х=а производные
всех порядков. Rn
- остаточный член в ряде Тейлора
определяется выражением
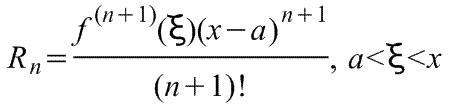
2)
k-тый коэффициент (при хk) ряда определяется формулой

3) Частным случаем ряда Тейлора является ряд Маклорена (=Макларена) (разложение происходит вокруг точки а=0)
при
a=0

члены ряда определяются по формуле

Условия применения рядов Тейлора.
1. Для того, чтобы функция f(x) могла быть разложена в ряд Тейлора на интервале (-R;R) необходимо и достаточно, чтобы остаточный член в формуле Тейлора (Маклорена (=Макларена)) для данной функции стремился к нулю при k→∞ на указанном интервале (-R;R).
2. Необходимо чтобы существовали производные для данной функции в точке, в окрестности которой мы собираемся строить ряд Тейлора.
Свойства рядов Тейлора.
-
Если f есть аналитическая функция, то ее ряд Тейлора в любой точке а области определения f сходится к f в некоторой окрестности а.
-
Существуют бесконечно дифференцируемые функции, ряд Тейлора которых сходится, но при этом отличается от функции в любой окрестности а. Например:

Ряды Тейлора применяются при аппроксимации ( приближение - научный метод, состоящий в замене одних объектов другими, в том или ином смысле близкими к исходным, но более простыми) функции многочленами. В частности, линеаризация ((от linearis — линейный), один из методов приближённого представления замкнутых нелинейных систем, при котором исследование нелинейной системы заменяется анализом линейной системы, в некотором смысле эквивалентной исходной.) уравнений происходит путём разложения в ряд Тейлора и отсечения всех членов выше первого порядка.
Таким образом, практически любую функцию можно представить в виде полинома с заданной точностью.
Примеры некоторых распространенных разложений степенных функций в ряды Маклорена (=Макларена,Тейлора в окрестностях точки 0) и Тейлора в окрестностях точки 1. Первые члены разложений основных функций в ряды Тейлора и Макларена.
Примеры некоторых распространенных разложений степенных функций в ряды Маклорена( =Макларена, Тейлора в окрестностях точки 0)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Примеры некоторых распространенных разложений в ряды Тейлора в окрестностях точки 1
|
|
|
|
|
|










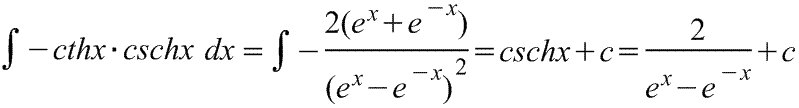



 Производная
косеканса
Производная
косеканса Производная
секанса
Производная
секанса Производная
арксинуса
Производная
арксинуса Производная
арккосинуса
Производная
арккосинуса Производная
арксинуса
Производная
арксинуса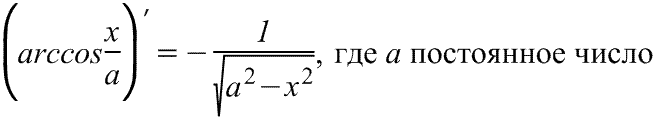 Производная
арккосинуса
Производная
арккосинуса Производная
арктангенса
Производная
арктангенса Производная
арккотангенса
Производная
арккотангенса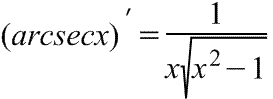 Производная
арксеканса
Производная
арксеканса Производная
арккосеканса
Производная
арккосеканса Производная
арксеканса
Производная
арксеканса Производная
арккосеканса
Производная
арккосеканса Производная
гиперболического синуса
Производная
гиперболического синуса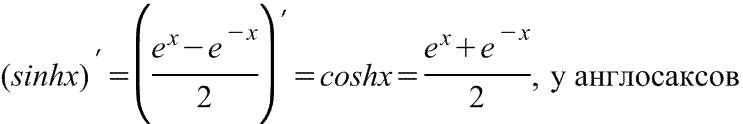 Производная
гиперболического синуса в английской
версии
Производная
гиперболического синуса в английской
версии Производная
гиперболического косинуса
Производная
гиперболического косинуса Производная
гиперболического косинуса в английской
версии
Производная
гиперболического косинуса в английской
версии Производная
гиперболического тангенса
Производная
гиперболического тангенса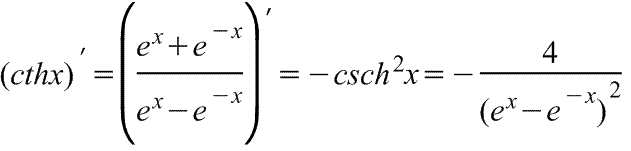 Производная
гиперболического котангенса
Производная
гиперболического котангенса Производная
гиперболического секанса
Производная
гиперболического секанса Производная
гиперболического косеканса
Производная
гиперболического косеканса