
- •Вариант: Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Контрольная работа №1
- •Контрольная работа №2
- •Литература
- •Экзаменационные вопросы (ликв. Академ. Задолженности)
- •Литература
- •Экзаменационные вопросы (ликв. Академ. Задолженности)
Контрольные работы Факультет: УиА по Математике I семестр Профиль: АСОиУ гр. 3422, 24 Заочная форма обучения Преподаватель: д.ф.-м.н., проф. Мухарлямов Р.Г.
Вариант: Контрольная работа №1
|
Задание 1. Выполнить действия над матрицами:
|
(А
+ В
)(2Е
– А),
где
| |
|
Задание 2. Решить систему уравнений: а) методом Крамера; б) методом Гаусса; в) матричным способом. |
| |
|
Задание 3.Найти общее решение одно- родной системы и записать общее решение через фунда- ментальную систему реше- ний: |
| |
Задание
4.
Даны
точки A(3;3;-2),
B(0;-3;4),
C(0;-3;0),
D(0;2;-4).
Найти

Задание 5. Задан треугольник с вершинами А(1;-2;8), В(0;0;4), С(6;2;0). Вычислить его площадь
и
высоту

Задание
6.
Вычислить объем тетраэдра ОАВС,
если

Задание 7. Написать уравнение прямой, проходящей через точку пересечения прямых
2х–3у–1 = 0 и 3х + у – 7 = 0 перпендикулярно к прямой у = 2х + 5.
Задание
8.
Две грани
куба лежат на плоскостях
 ,
, .
.
Вычислить объем этого куба.
Задание 9. Найти расстояние от центра окружности х2 + у2 + 2у =0 до прямой
у = 2 (2 – х).
Контрольная работа №2
Задание
1.
Даны комплексные числа
 и
и .
Найти:
.
Найти:
а)
 б)
б)
 в)
в)
 г)
г)
 д)
д)

Задание
2.
Применяя
формулу Муавра, найти
 :Z
= 1
+ i,
n=10.
:Z
= 1
+ i,
n=10.
Задание
3.
Найти пределы: а) ;
б)
;
б) ;
;
в)
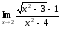 ;
г)
;
г)
 ;
д)
;
д) .
.
|
Задание 4. Найти производные следующих функций: |
а)
|
|
Задание 5. Используя формулу логарифмического диф ференцирования, найти производные следующих функций: |
а)
|
Контрольная работа №1
|
Задание 1. Выполнить действия над матрицами: |
А
– (Е
+ 2В)В,
где
| |
|
Задание 2. Решить систему уравнений: а) методом Крамера; б) методом Гаусса; в) матричным способом. |
| |
|
Задание 3.Найти общее решение одно- родной системы и записать общее решение через фунда- ментальную систему реше- ний: |
| |
Задание
4.
Вектор
 перпендикулярен
векторам
перпендикулярен
векторам и
и и удовлетворяет усло- вию
и удовлетворяет усло- вию .
Найти координаты вектора
.
Найти координаты вектора .
.
Задание
5.
Даны векторы
 Вычислить модуль вектора
Вычислить модуль вектора и площадь треугольника, построенного
на векторах
и площадь треугольника, построенного
на векторах и
и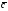 .
.
Задание 6. Вычислить объем тетраэдра с вершинами в точках А(2;-3;5), В(0;2;1), С(-2;-2;-3), D(3;2;4).
Задание 7. Даны уравнения двух сторон прямоугольника 2х–3у+5=0, 3х + 2у – 7 =0 и одна из его вершин А (2;–3). Составить уравнения двух сторон этого прямоугольника.
Задание
8.
Показать,
что прямая
 лежит в плоскости
лежит в плоскости .
.
Задание 9. Определить, как расположена прямая 2х–у–3=0 относительно окружности х2+у2–3х+2у–3=0.
Контрольная работа №2
Задание
1.
Даны комплексные числа
 и
и .
Найти:
.
Найти:
а)
 б)
б) в)
в) г)
г) д)
д)
Задание
2.
Применяя
формулу Муавра, найти
 :Z
= 1 – i,
n
= 10.
:Z
= 1 – i,
n
= 10.
Задание
3.
Найти пределы: а)
 б)
б)
в)
 г)
г) д)
д)
|
Задание 4. Найти производные следующих функций: |
а)
|
|
Задание 5. Используя формулу логарифмического диф ференцирования, найти производные следующих функций: |
а) |

 ,
,


 ; б)
; б) .
. ;
б)
;
б) .
. ,
,


 б)
б)

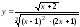 б)
б)