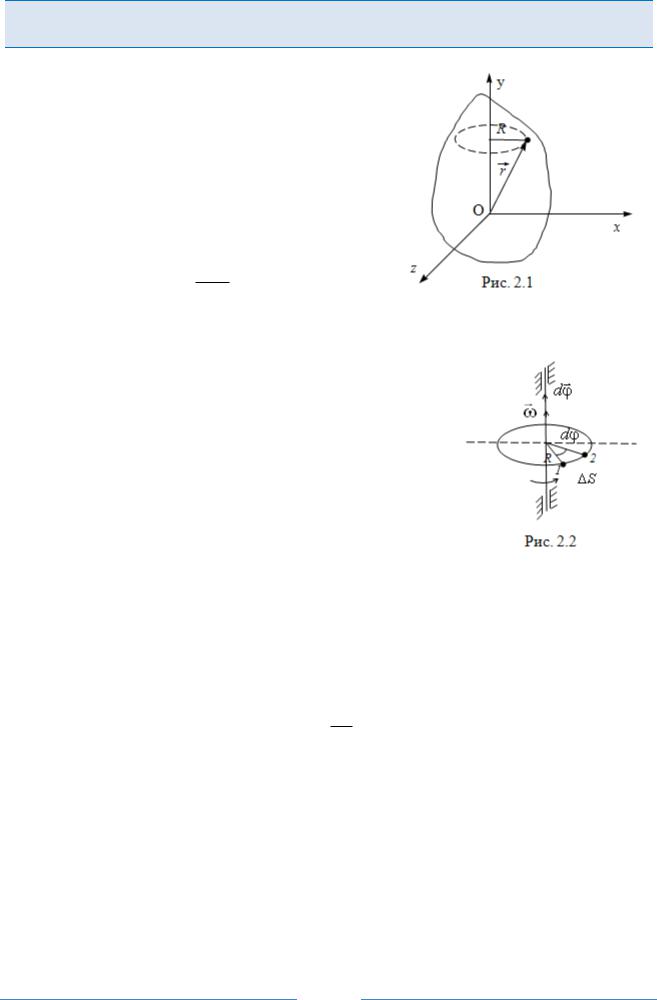
ГЛАВА 2 Кинематика вращательного движения

Рассмотрим твердое тело, которое вращается вокруг неподвижной оси (рис. 2.1). Все точки тела при вращении описывают окружности разных радиусов R, центры которых лежат на оси вращения. За время одного полного оборота T любая точка проходит путь равный 2πR. Следовательно, различные точки тела за время одного оборота проходят разные пути и двигаются с разными линейными скоростями:

V = 2TπR .

Введем характеристики, описывающие вращательное движение твердого тела как единого целого: вектор углового элементарного перемещения ϕ, уг-

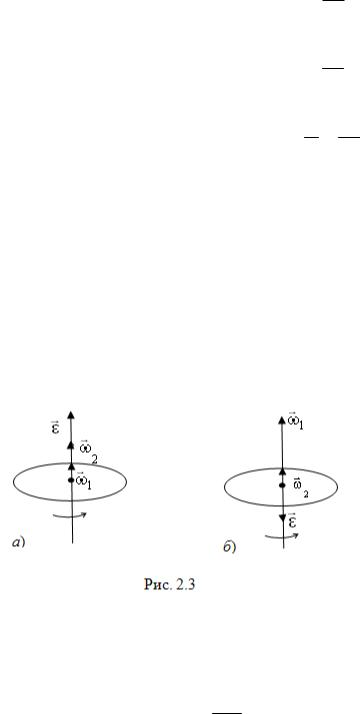
ловую скорость ωr , угловое ускорение ε. Пусть некоторая точка движется по окружности радиуса R (рис. 2.2). Ее положение через промежуток времени ∆t зададим углом ∆ϕ. Элементарные (бесконечно малые) углы поворота рассматривают как векторы. Модуль вектора dϕ равен углу поворота, а его направление сов-

падает с направлением поступательного движения острия винта, головка которого вращается в направлении движения точки по окружности, т.е. подчиняется правилу правого винта.

2.1. Угловая скорость

Угловой скоростью ωr называется векторная величина, численно равная первой производнойr угла поворота по времени, совпадающая с направлением вектора dϕ:

ωr = ddtϕ .

Единицей измерения угловой скорости в системе СИ является радиан в

где ∆ϕ − угол поворота за время ∆t.

9

Равномерное вращение можно характеризовать периодом обращения T, под которым понимают время, за которое тело делает один оборот, т.е. поворачивается на угол 2π. В этом случае

ω= 2Tπ,

отсюда

T = 2ωπ .

Число оборотов в единицу времени ν равно

ν = T1 = 2ωπ .

Следовательно,

ω = 2πν.

Угол поворота

ϕ = 2πN ,

где N − число оборотов твердого тела.

2.2. Угловое ускорение

Вектор ωr может изменяться с течением времени как за счет изменения величины скорости вращения тела вокруг оси, так и за счет изменения направления вращения. Угловым ускорением ε называется векторная величина, равная первой производной вектора

угловой скорости по времени:

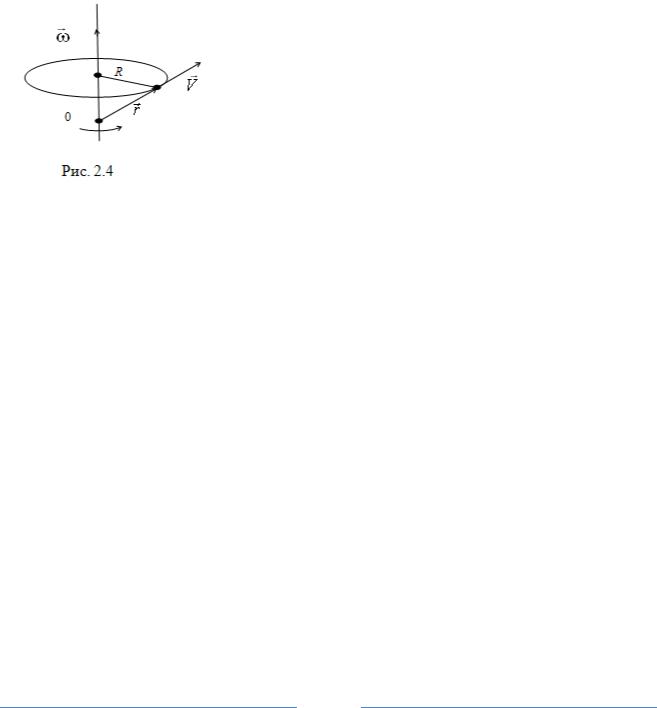
(рис.2.3). Единицей измерения углового ускорения в системе СИ является радиан на секунду в квадрате радc2 .

Равнопеременное вращение можно описать системой уравнений:

где ω0 = ω(t = 0) - начальная угловая скорость; ϕ0 = ϕ(t = 0) - начальный угол поворота.

2.3. Связь линейных и угловых характеристик

Установим связь между модулями линейной и угловой скоростей:

где ε − модуль углового ускорения. В результате aτ = εR .

Таким образом, линейная скорость V , нормальное an и тангенциальное arτ ускорения растут линейно с увеличением расстояния от точки до оси враще-

x = A + Bt +Ct3 , где A = 4м, B = 2м/с, C = 0,2м/с3. Найти: 1) положение точки в моменты времени t1 = 2с, t2 = 5с; 2) среднюю путевую скорость Vср за время, протекшее между этими моментами; 3) мгновенные скорости V1 и V2 в указанные моменты времени;4) среднее ускорение aср за указанный промежуток времени; 5) мгновенные ускорения a1 и a2 в указанные моменты времени.

11