
Проектирование сварных конструкций / metallicheskie_konstrukcii / Лекция 06
.pdf
Лекция № 6. Тема: «Предельные состояния и расчет внецентренно-растянутых и внецентренно-сжатых элементов»
Предельные состояния рассматриваемых стержней определяются прочностью, развитием пластических деформаций и потерей устойчивости.
Предельные состояния по прочности внецентренно-растянутых стержней установлены для стержней из стали высокой прочности (у которых отсутствует площадка текучести), а для стержней из стали обычной прочности – при динамических нагрузках. В этих случаях расчет производится по упругой стадии, и предельное состояние наступает тогда, когда наибольшие фибровые напряжения достигают предела текучести. Расчет на прочность таких стержней производится по формуле
N |
± |
M |
x |
y ± |
My |
x ≤ R |
γ |
|
, |
(6.1) |
|
|
|
|
c |
||||||
An |
|
Jxn |
Jyn |
y |
|
|
|
|||
|
|
|
|
|
|
|||||
где x и у – координаты рассматриваемой точки сечения относительно его главных осей. Предельные состояния по развитию пластических деформаций установлены для стержней
из пластических сталей при действии статических нагрузок. В этом случае предельное состояние определяется шарниром пластичности, который развивается следующим образом (в соответствии с диаграммой Прандтля): при увеличении М и N на одной из сторон сечения стержня фибровые напряжения достигают Ryn и останавливаются в своем развитии. Напряжения в других фибрах продолжают расти, пока, наконец, напряжения на другой стороне сечения не достигнут Ryn. После чего пластичность распространяется на все фибры сечения и образуется шарнир пластичности.
Ì |
à) σ < Ryn |
á) |
â) σ = Ryn |
|
|
|
|
A1 γc Ryn |
|
|
N |
|
|
e |
|
|
A1 γc Ryn |
|
|
|
|
A γ R |
||
|
|
|
1 |
c yn |
|
σ = Ryn |
σ = Ryn |
σ = Ryn |
|
Очевидно, что разность площадей эпюр напряжений, умноженная на Ryn, равна предельной продольной силе:
NМ |
= R |
уп |
А . |
(6.2) |
|
пр |
|
2 |
|
||
Предельный момент |
|
|
|
|
|
M N |
= R |
уп |
А е. |
(6.3) |
|
пр |
|
|
1 |
|
|
В пластической стадии напряжения от N и М можно четко разделить.
Для оценки несущей способности внецентренно напряженного стержня при шарнире пластичности введем 4 величины:
NпрМ - предельная продольная сила при наличии момента;
Nпро - предельная продольная сила при отсутствии момента, Nпро = A Rуп ;
МпрN - предельный момент при наличии продольной силы;
Мпро - предельный момент при отсутствии продольной силы, Мпро = Сx Wнт Rуп
Очевидно, что
NМ |
=ν < 1 |
|
М N |
= µ < 1 |
|
|
пр |
и |
пр |
(6.4) |
|||
Nо |
М о |
|||||
|
|
|
|
|||
пр |
|
|
пр |
|
|
Связь между этими соотношениями при шарнире пластичности выражается параболой и записывается в общем виде:
ν n + µ =1, |
(6.5) |
где n – показатель степени, зависящий от формы поперечного сечения стержня (для двутавра n=1,5).
Таким образом, соотношение между ν и µ примет вид:
1

|
N |
|
|
n |
M |
x |
|
|
|
|
|
|
|
|
|
+ |
|
|
|
|
≤1 |
(6.6) |
|
|
γ |
|
|
|
|
γ |
|
||||
|
A R |
|
|
C W |
|
R |
c |
|
|||
|
n y |
|
c |
x xn,min |
y |
|
|
||||
где Сх – коэффициент, учитывающий развитие пластических деформаций в сечении.
Это и есть расчетная формула на прочность внецентренно нагруженного стержня с учетом развития пластических деформаций (внецентренно растянутого).
Поверочная формула для стержней, которые рассчитываются по упругой стадии
N |
+ |
Mx |
≤ γ |
R |
|
|
|
y |
|||
An |
|
c |
|
||
Wxn,min |
|
|
|||
При расчете стержней на устойчивость (внецентренно сжатых) различают два вида работы стержней: внецентренное сжатие и сжатие с изгибом.
N |
|
|
|
N |
|
|
1) |
|
2) |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
f |
P |
Работа этих стержней несколько отличается друг от друга. Но в целях упрощения расчетов сжато-изогнутые стержни при потере устойчивости рассматривают как внецентренно сжатые с эксцентриситетом e=M/N. При внецентренном сжатии с самого начала приложения нагрузки возникает изгиб стержня, который увеличивается с ростом нагрузки. Величина нагрузки, при которой изгибные деформации растут при постоянном ее значении или даже уменьшении, называется критической Nu.
N |
|
B |
|
|
C |
u |
|
|
N |
|
|
|
O |
f |
|
|
При постепенном повышении нагрузки напряжения более нагруженных фибр переходят в пластическую стадию; нейтральная ось при этом смещается в сторону выпуклых волокон (так же, как и при центральном сжатии). Критическое состояние перехода стержня из устойчивого в неустойчивое положение располагается в пределах развития пластических деформаций по сечению.
В современной теории расчета внецентренно сжатых стержней при определении критической силы Nu принимается допущение о том, что в процессе возрастания нагрузки и в
2

момент потери устойчивости влияние разгрузки не учитывается, т.е. рассматривается нелинейно упругий металл, как в условиях догрузки, так и разгрузки.
Критическая сила
N |
|
= |
π 2ЕJ |
t , |
(6.7) |
|
и |
l2 |
|||||
|
|
|
|
где EJt = ∫Et y2dA - приведенная жесткость стержня,
A
Еt – касательный модуль для диаграммы работы металла стержня.
Для определения приведенной жесткости ЕJt необходимо знать эпюру напряжения в наиболее нагруженном сечении стержня, характер которой будет зависеть от гибкости стержня, эксцентриситета и формы сечения. Поэтому критические напряжения внецентренно сжатого стержня зависят от трех факторов:
1)от приведенной гибкости λ = λ 
 Ry
Ry 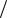 E ;
E ;
2)от формы поперечного сечения стержня, которая учитывается коэффициентом η («этта»). Этот коэффициент учитывает степень распространения пластических деформаций по сечению.
Кривые критических напряжений σкрвн в функциях гибкости и относительного эксцентриситета для
различных форм сечений подобны. Это дает возможность переходить от кривых для прямоугольного сечения к кривым для других типов сечений умножением на переходный коэффициент η;
3) от относительного эксцентриситета
m = е/ ρ ,
где е – абсолютный эксцентриситет;
ρ – ядровое расстояние ρ =W / A (W – момент сопротивления сечения для наиболее сжатого волокна).
Рассмотренный выше случай характерен тем, что потеря устойчивости стержня происходит в плоскости действия момента; происходит изгибная форма потери устойчивости.
σ вн
Обозначая через ϕе = кр , получим расчетную формулу при проверке на устойчивость в
Ry
плоскости действия момента:
N |
≤ R γ |
|
, |
(6.8) |
|
|
|
||||
ϕe |
A |
y |
c |
|
|
|
|
|
|
||
где ϕе – коэффициент снижения расчетных сопротивлений при внецентренном сжатии, зависящий
|
|
|
|
|
|
|
Ry |
|
от условной |
|
гибкости λ = λ |
и приведенного относительного эксцентриситета |
|||||
|
E |
|||||||
|
|
|
|
|
|
|
|
|
m =η m =η |
e |
=η |
M W |
. |
|
|
||
ρ |
|
|
|
|||||
ef |
|
N A |
|
|
||||
|
|
|
|
|
|
|
|
|
3
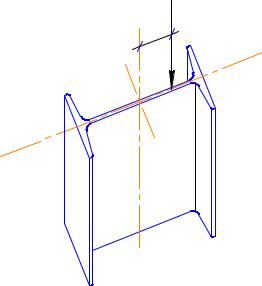
N
|
e |
|
x |
y |
x |
|
y
Для приведенного рисунка плоскость действия силы – это плоскость стенки двутавра.
При любых расчетах на устойчивость площадь сечения принимается брутто, т.е. с учетом площадей отверстий.
Внецентренно сжатые стержни, имеющие различные жесткости в обоих главных плоскостях (Jх>Jу), и момент в плоскости большей жесткости, могут потерять устойчивость в направлении меньшей жесткости. При этом стержень не только изгибается, но и закручивается и теряет устойчивость по изгибно-крутильной форме. Эта форма потери устойчивости является общим случаем и называется также пространственной. Переход разных частей сочетания в пластическую стадию работы происходит не одновременно и всегда сопровождается закручиванием стержня. При этом оставшаяся рабочая часть (упругое ядро) меняет свою форму; центр изгиба смещается и получается эксцентриситет, приводящий к выходу стержня из работы по изгибно-крутильной форме.
Устойчивость стержня из плоскости действия момента проверяют по формуле:
N |
≤ R |
γ |
|
, |
(6.9) |
|
c |
||||
Cϕy A |
y |
|
|
|
|
|
|
|
|
|
где С – коэффициент приведения ϕу к условиям пространственной потери устойчивости (учитывает влияние момента на потерю устойчивости из плоскости действия момента).
Наиболее характерна потеря устойчивости по изгибно-крутильной форме в упругой области для тонкостенных незамкнутых сечений (типа двутавров, швеллеров и др.)
4
