2. Линии влияния усилий стержневых ферм

Рис.8.72

При загружении ферм движущимися нагрузками, например тележкой крана, целесообразно определять усилия в стержнях методом линий влияния. Линии влияния усилий стержней фермы выражают зависимость величины усилий в стержнях от положения груза, равного единице, на ферме. Таким образом, для каждого стержня фермы сроится соответствующая линия влияния.

Груз может перемещаться как по верхнему, так и по нижнему поясу фермы в соответствии с загружениями реальными силами.

По продольным брускам перемещается груз, равный единице, воспринимаемый фермой через поперечные брусья. Таким образом, осуществляется передача нагрузки на ферму по узлам.

В действительности такая надстройка нередко осуществляется в сооружениях. Если же она в действительности отсутствует, то для построения линий влияния продольных усилий поясов следует допустить, что она все же имеет место.

Рассмотрим линии влияния усилий в стержнях фермы с параллельными поясами, которая опирается на две опоры (Рис. 8 .72, а).

Производим последовательно разрезы III-IIIиII-II(Рис. 8 .72, б).

Рис.8.73 Линия влияния усилия в стержне 23.

Для построения линии влияния 23 рассмотрим уравнение равновесияМ_3’=0.

При грузе, находящемся справа от разрезанной панели III-III, уравнение равновесия для левой части фермы будет

A∙3d – 23 h = 0;

При х = 0 А =1 и

При х = l А = 0 13 = 0

Проводим правую линию влияния 23, которая верна при условии, что груз находится на участке от узла 6' до узла 3'.

При грузе, находящемся слева от разрезанной панели III-III, уравнение равновесия для правой части фермы будет

B∙3d – 32∙h = 0 откуда

Аналогичным образом находим левую линию влияния, которая верна при грузе, находящемся на участке от узла 0' до узла 2'.

При перемещении груза от 2' до 3' линия влияния изменяется по закону прямой, изображенной на Рис. 8 .73, являющейся продолжением левой линии влияния.

Рис.8.74 Линия влияния усилия в стержне 2'3'.

Аналогичным образом пишем условия равновесияМ₂=0 и строим линию влияния 2'3' (Рис. 8 .74).

Если груз находится справа от 3' то 2’3’∙h+A∙2d=0 откуда2’3’=, в т.0’А=Р=1, в т.6’ А=0.

Если груз находится слева от 2' то 2’3’∙h+В∙4d=0 откуда2’3’=, в т.6’ В=Р=1, в т.0’ В=0.

Рис.8.75 Линия влияния усилия в стержне 23'.

Определение усилия в раскосе 23'.

При грузе, находящемся справа от разрезанной панели, уравнение равновесия для левой части фермы запишется так:

При х = 0: 23’=;

При х = L: 23’ = 0

Проводим правую линию влияния 23', которая верна при грузе, находящемся на участке от узла 6' до узла 3' (Рис. 8 .75).

При грузе, расположенном слева от разрезанной панели, уравнение равновесия для правой части фермы запишется так:

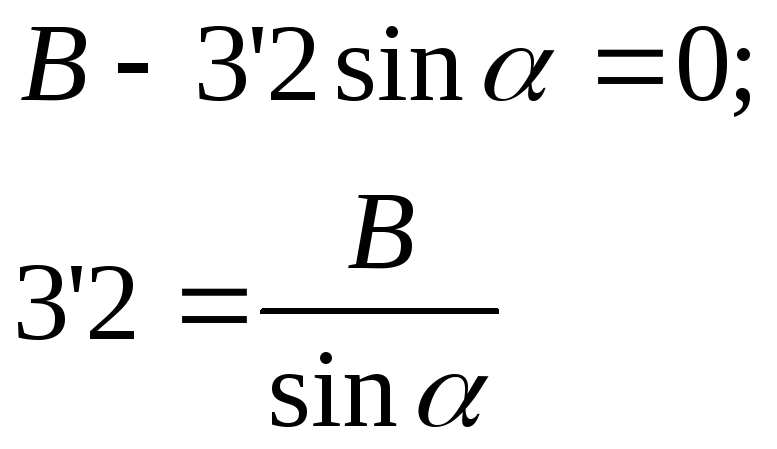
При х=0: 3’2=0

При х=l:

Левая линия влияния верна при грузе, находящемся на участке 0'2'.

Линия влияния 1'2' строится из рассмотрения условия равновесия узла 2'

ΣX = 0откуда следует, что 2’1’=2’3’.

Линия влияния 0’1’ строится с учетом условия равновесия узла 0'

ΣX = 0откуда следует, что 0’1’=0.

Рис.8.76 Линия влияния усилия в стержне 12.

Для построения линии влияния 12 проводится разрез II-IIи пишутся условия равновесияΣM_1'=0.

Очертание линии влияния 12 показано на Рис. 8 .76.Из условия равновесия ΣХ=0 в узле 1 следует, что линия влияния 10 равна линии влияния 12.

Рис.8.77 Линия влияния усилия в стержне 1'2.

Для построения линии влияния 1'2 следует использовать условие равновесия ΣУ=0 в сечении между 1 и 2.

При грузе, находящемся справа от разрезанной панели

A – 1’2sin α = 0

При х=0:;

при х=L: 1'2=0.

проводим правую линию влияния 1’2, которая верна при грузе, находящемся на участке от узла 6’ до узла 2' (Рис. 8 .77).

При грузе, находящемся слева от разрезанной панели II–II

B + 21’ sinα = 0

При х=L: 21’

при х =0: 21’=0.

Проводим левую линию влияния на участке 0’1’. При перемещении груза от 1' до 2' линия влияния определяется уравнением прямой, изображенной на Рис. 8 .77 пунктирной линией.

Аналогичным путем строим линию влияния усилия в стержне 01'.

Построим линию влияния усилия в стойке 11'

Из условия равновесия сил, приложенных в узле 1, ΣY=0 вытекает, что усилие 11'=0.

Ординаты линии влияния стойки 33' также равны нулю.

Рис.8.78 Линия влияния усилия в стержне 22'.

При построении линии влияния усилия в стержне 22' следует рассмотреть условия равновесияΣY=0 в узле 2'.

Если груз находится вне второй и третьей панелях, то усилие 2'2=0.

Если груз находится в узле 2', то условие ΣY =0пишется таким образом: —2'2—1=0, при этом 2'2=—1 (Рис. 8 .72, и).

При перемещении груза на участках 1'2' и 23' линия влияния имеет очертание треугольника (Рис. 8 .78).

Рис.8.79 Линия влияния усилия в стержне 22'.

Линия влияния усилия в опорной стойке 00' находится из условия равновесияΣY =0в узле 0' (Рис. 8 .72, з).

При отсутствии груза на первой панели 0'0=0.

При нахождении груза в узле 0' уравнение равновесия запишется так:

-1-0’0 = 0 откуда 0'0 = — 1

При перемещении груза от узла 0 до узла 1 линия влияния усилия в стержне 00' определяется уравнением прямой, изображенной на Рис. 8 .79 пунктирной линией.