7.2. Усилия, действующие на зубчатые передачи.

Усилия, которые действуют в прямозубых зубчатых передачах

Рис. 7.5. Усилия, действующие на зуб

b_w—ширина зубчатого колеса,q—удельная нагрузка, распределенная по линии контакта зубьев,F_n—полное усилие, действующее на зуб, оно обязательно действует по линии зацепления,a_w—угол зацепления.

Перенесем F_nпо линии действия до пересечения с осью симметрии зуба.

Разложим: F_T —или окружное усилие, F_r—радиальное усилие.

F_T=2T/d; T—момент,Т=F_Td/2(7.12)

F_r=F_Ttg α_w; F_n=F_T/cosα_w (7.13)

Рис. 7.6. Усилия в прямозубой зубчатой передаче

Усилия, действующие в косозубых и шевронных передачах. В следствие того, что в косозубых зубчатых передачах зуб наклонен под углом β, поэтому в косозубых зубчатых передачах дополнительно возникает осевое усилие.

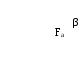
Рис. 7.7. Усилие в косозубой передаче

Т = 9550 Р / n; (нм), гдеР—мощность (КВт) (7.14)

F_T = 2T₁ / d₁(7.15)

Т_а = F_T tgβ, β = 8⁰ … 20⁰(7.16)

Одним из недостатков косозубых зубчатых передач является возникновение осевого усилия. Причем с увеличением угла наклона зубьев это усилие растет

Fr=F_Ttgα_w /cosβ; F_n=F_T/cosβcosα_w, (7.17)

α_w—угол зацепления в нормальном сечении; β—25⁰…40⁰.

Шевронная передача. Шевронные зубчатые колеса применяют в тяжело нагруженных зубчатых передачах

Рис. 7.8. Шевронная передача

Расчетная нагрузка. При расчете зубчатых передач на прочность необходимо за расчетную нагрузку принимать максимальное значение удельной нагрузки распределенной по линии контакта зубьев. При этом учитывая ряд дополнительных обстоятельств

g_kα=(F_n/L_Σ) КβК_VКα, (7.18)

где Кα—коэффициент, учитывающий одновременное участие в передаче нагрузки нескольких пар зубьев, Кβ—коэффициент, учитывающий распределение нагрузки по ширине венца, К_V—коэффициент динамической нагрузки,L_Σ—суммарная длина контактных линий,

L_Σ=(bw/cosβ)/Кεεα,(7.19)

где bw—ширина зубчатого колеса, β—угол наклона зубьев,

Кε—коэффициент, учитывающий перекрытие зубьев,—коэффициент торцевого перекрытия,

g=(F_T Кβ К_Vcosβ Кα)/ cosβcosα_w bwКε εα,(7.20)

Удельная расчетная окружная сила

W_t=(F_T/ bw)/ Кβ К_VКα(7.21)

где F_T—окружная сила,

g=w_t/ Кεεα cosα_w,(7.22)

где Кβ—коэффициент неравномерности распределения нагрузки,

К_{V —} коэффициент динамической нагрузки, Кα—коэффициент, учитывающий распределение нагрузки между зубьями (сколько пар зубьев в зацеплении одновременно).

При нагружении зубчатых передач валы упруго изгибаются и зацепление колес происходит в первой точке. Если бы зубья были бы абсолютно жесткими, то контакт между зубьями был бы в первой точке.

Коэффициент неравномерности распределения нагрузки — К_β. Вследствие того, что зубья прирабатываются и деформируются, контакт зубьев происходит по полной длине зуба, то при этом нагрузка по длине зуба распределяется неравномерно.

Рис.7.9. Неравномерность распределения нагрузки

К_β=g_max/g_средн(7.23)

Неравномерность распределенения нагрузки возрастает с увеличением ширины зубчатых колес b_w. Неравномерность распределения нагрузки между зубьями неодинакова. При расчете зубьев на прочность по контактным напряжениям ко всем буквенным обозначениям приписывается индекс Н (Герц) и при расчете на изгиб индексF (К_нβ и К_Fβ).Коэффициент распределения нагрузки по ширине венца, без учета закручивания широких шестерен, равен

Кнβ=1+(0,4b_w²C_Σγ/ F_T) К_w; К_Fβ=1+( К_Fβ⁰-1)К_w,(7.24)

C_Σ—суммарная удельная жесткость сопряженных зубьев,γ=γ_w+γ_Δ —суммарный угол перекоса зубьев, γ_w — угол перекоса зубьев, вызванный упругими деформациями всех деталей: подшипников, валов, зубьев; γ_Δ—угол перекоса зубьев, вызванный неточностью изготовления;К_w—коэффициент, учитывающий приработку зубьев;К_a—среднее значение коэффициента внешней нагрузки, который выделен в самостоятельный коэффициент, что уменьшает вероятность недоучета внешней динамики;F_T—окружное усиление.

Среднее значение К_βопределяется по приведенной формуле, где вместоγ_∆подставляют среднее значениеγ_∆, тогда составляющая, пропорциональная упругому перекосу зубьев, может рассматриваться как детермированная, а пропорциональная погрешности изготовления как случайная. В среднем можно принять детерминированную составляющую равной 2/3 от среднего относительного приращения нагрузки, т.е.2/3 (_β -1),тогда поле рассеяния дополнительной относительной случайной нагрузки равно2/3(К_β -1),полагая, что поле рассеяния перекрываетсяδсредними квадратическими отклонениями, получаем выражение для коэффициента вариации.

v_β=1/9 (_β-1)/К_β(7.25)

Коэффициент, учитывающий распределение нагрузки между зубьями. Коэффициент К_α, учитывающий участие в передаче нагрузки второй пары зубьев. Введение в расчеты коэффициентаК_αупрощает расчеты и уменьшает вероятность ошибок при учете эффекта много парности зацепления. Максимальное значениеК_αравно единице и соответствует наиболее неблагоприятному случаю—работе только одной пары зубьев; минимальное значениеК_α, соответствует работе точных зубчатых передач.

Для прямозубых передач —К_αmin =4 – εα/3;

Для косозубых передач —К_αmin=1/εα;

К_Fα=0,42+(0,58×∆α/F_T), (7.26)

εα -- коэффициент перекрытия,

торцевого εα=[1,88-3,2(1/Z₁+1/Z₂)] ×cosβ. ,осевогоεα=b_w×sinβ/π×mn. (7.27)

Среднее значение коэффициента К_αдля прямозубых передач выбирают в зависимости от степени точности изготовления.

Таблица 7.1.

Степень точности изготовления

Твердость шестерни и колеса.	Степень точности по ГОСТу 1643-81
	5	6	7	8	9
Н1>НВ350 Н2<НВ350	4-εα/3	0,8	0,9	1,0	1,0
Н1≤ НВ350 Н2≥ НВ350	4-εα/3	4-εα/3	0,8	0,9	1,0

Среднее значение коэффициента К_αдля точных косозубых колес принимаемК_α=1/ εα, для косозубых колес 6,7,8,9 степени точности величину определяют

К_Нα=1/εα[(0,942-0,002×V)+(0,058+0,005×V) ×1,4^n-6] (7.28)

К_Fα=[4+(εα-1) (n-5)]/4×εα (7.29)

где n—степень точности;V—окружная скорость.

Для определения коэффициента V_αвариации коэффициентаК_αпредставляем его общей для прямозубых и косозубых колес зависимостью

К_α=а_α+b_α+∆_α,(7.30)

где а_α—предельная величина, зависящая от коэффициента перекрытия.

b_α—коэффициент пропорциональности, зависящий от нагрузки, жесткости, приработки зубьев.

∆_α—разность шагов зацепления, рассматриваемая как случайная величина.

V_α=[( К_α- а_α)/К_α] ×V_∆α(7.31)

Обычно берут а_α=0,55, аV_∆α=0,25.

В практических расчетах берут

Таблица 7.2.

Коэффициент V_αвариации коэффициентаК_α

Кα	0,95	0,9	0,85	0,8	≤0,8
Vα	0	0,05	0,08	0,05	0

Обычно V_hα=0,05

Коэффициент динамической нагрузки — К_V. При изготовлении зубчатых колес неизбежны погрешности в размерах. Погрешности в точке зацепления при нарезании зубьев является причиной непостоянство мгновенного передаточного числа следовательно, если

=const, ≠const,d_w/d_t ≠ 0. Это означает, что в данной системе возникает ускорение. Таким образом, в зацеплении появляется динамический момент

T_g=Y×(d/dt),(7.32)

где Y—момент инерции вращающихся ведомых пар.

Коэффициент динамической нагрузки зависит от погрешности шага при изготовлении, а это в зависимости от колеса точности зубчатых колес, от окружной скорости зацеплений, от жесткости деталей зубчатой передачи. При расчете по контактным напряжениям и напряжениям изгиба, значения К_нvиК_Fvразличны. Коэффициент неравномерности распределенной нагрузки и коэффициент динамической нагрузки выбираются по справочным данным. Случайный характер коэффициентаК_v, учитывающего динамическую нагрузку, определяется случайностью двух величин: разности шагов зацепления∆_αи коэффициентомφ, который учитывает снижение динамической нагрузки вследствие кратковременности ее действия и приработки. Связь междуК_vи случайными величинами ∆_αи φ выражается

К_v=1+с×X, (7.33)

где X=φ×, с—коэффициент, пропорциональный окружной скорости приведенный к массе и обратно пропорциональный передаваемой удельной нагрузке.φ—коэффициент, учитывающий приработку и специфику влияния динамической нагрузки на выносливость.

Коэффициент вариации величины К_vопределяется по формуле

V_v= (К_v-1/ К_v) V_x(7.34)

Коэффициент вариации случайной величины X, рассматриваемой как произведение двух случайных величинφи равен

, (7.35)

где V_φ—коэффициент вариации величиныφ. Тогда

V_v=(К_v-1/ К_v) (7.36)

Обычно при Н>НВ350 φ=0,75…0,5, приН≤НВ350 φ=0,5…0,25.

Обычно V_HV=0,17 (К_HV-1)/ К_HV.