
Насосы С11АЭ,11МТ,11ТС / 11-МТ / 2.Ксерокопии книг / 03.Книга.ГЦН_АЭС
.pdf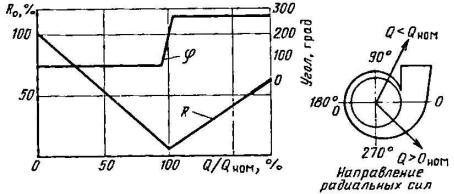
следствием чего являются значительное утяжеление, усложнение и удорожание конструкции в целом.
Рис. 6.7. Зависимость радиальной силы R и ее направления от относительного расхода
Q/Qном
Радиальная сила на рабочем колесе - основной компонент результирующей радиальной силы в насосе. На рис. 6.7 показана типичная зависимость радиальной силы по величине и направлению от подачи для ГЦН со спиральным отводом. Минимальное значение радиальной силы соответствует подаче, близкой к номинальной. Вблизи этого же значения подачи изменяется угол направления действия силы: при Q<Qном вектор радиальной силы направлен в сторону меньших, а при Q>Qном - боQльшихсечений спирального отвода согласно изменению характера распределения давления по окружности колеса.
В ГЦН с направляющим аппаратом указанная выще неравномерность имеет место вдоль каждой лопатки, а полная осевая симметрия потока за колесом также отсутствует. Следствием нарушения круговой симметрии в распределении давлений и скоростей за колесом и является появленне неуравновешенной поперечной силы, действующей на ротор насоса. Чем больше неравномерность, а она возрастает с удалением от расчетной подачи, тем больше и радиальная сила.
При оценке радиальных сил в ГЦН широкое применение находит формула, предложенная в [1, Введение] на основании исследования насосов средней быстроходности (для холодной воды ):
R = 0,1KHD2b'2. |
(6.4) |
В насосах со спиральным отводом для определения безразмерного коэффициента K рекомендована формула
K = 0,36[1 – ( Q/Qном)2], |
(6.5) |
241

а в насосах с кольцевым отводом
K = 0,36(Q/Qном). |
(6.6) |
Из выражений (6.4) и (6.5) следует, что максимальноезначение радиальной силы соответствует нулевой подаче, а минимальное (равное нулю) — номинальной подаче,
когда К = 0,36.
Однако зависимость (6.5) не отражает действительного характера течения во многих конструкциях центробежных насосов: при расчетном режиме R теоретически становится равной нулю, но практически и при расчетной подаче полная симметрия потока около колеса отсутствует, вследствие чего R ≠ 0.
Кроме того, рассчитанные по этим формулам данные значительно отличаются от экспериментальных. В связи с этим, учитывая важность выявления влияния конструкционных особенностей на радиальные силы, рассмотрим один из методов их определения применительно к ГЦН АЭС.
Расчетный способ позволяет определять радиальную силу, вызванную нарушением осевой симметрии потока на выходе из рабочего колеса в насосах с реальной геометрией отвода. Радиальную силу при известном распределении параметров потока на выходе из рабочего колеса можно определить по следующим формулам:
|
|
|
|
|
Rрад = Rx2 + Ry2 |
; |
|
(6.7) |
|
2π |
|
2π |
|
|
Rx = − ρhb3 r2 ∫ H ст cosϕ dϕ − ρb2 r2 |
∫Cm2 × |
|
||
0 |
|
|
0 |
|
× (Cm2 cosϕ + Cu 2 sinϕ )dϕ ; |
|
(6.8) |
||
2π |
|
2π |
|
|
Ry = − ρhb3 r2 ∫ H ст sin ϕ dϕ − ρb2 r2 |
∫Cm2 × |
|
||
0 |
|
|
0 |
|
× (Cm2 sinϕ − Cu 2 cosϕ )dϕ ; |
|
(6.9) |
||
Здесь Rx. Ry — проекции радиальной силы па оси |
координат; |
ρ — плотность |
||
перекачиваемой среды; g — ускорение свободного падения; r2 — |
наружный радиус |
|||
колеса; HCT — статическая часть напора; Cm2, Cu2 — |
проекции абсолютной скорости на |
|||
меридиональное направление и направление переносной скорости соответственно; b2 и b3
—ширина колеса в свету и с дисками соответственно.
Задача расчета радиальных сил сводится к определению параметров потока на выходе из рабочего колеса.
Разработан канд. техн. наук В. А. Бабиным.
242
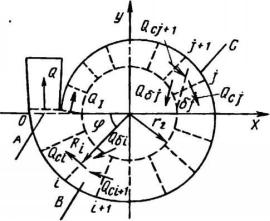
Рассмотрим усредненную за один оборот картину течения потока от выхода из колеса до входа в напорный патрубок отвода (рис. 6.8). Условно разобьем окружность рабочего колеса на N равных частей. Выходящий из рабочего колеса поток будем характеризовать усредненными по сечению проекциями абсолютной скорости (Cm2i, Cu2i) и напором, развиваемым данным участком (Hтi). Для нахождения Hтi воспользуемся уравнением Эйлера.
Соответственно разбивке окружности выхода рабочего колеса проведем разбивку спирального отвода. Кроме того, выделим в районе «языка» спирали дополнительный элемент А таким образом, чтобы жидкость в него непосредственно из колеса не поступала
(рис. 6.8).
Рис. 6.8. Схема разбиения отвода и
выходной окружности |
рабочего |
колеса: |
|
А — дополнительный элемент |
дли расчета |
потерь на входе в напорный патрубок; В и С — соответственно элементы со слиянием и разделением потоков; Qi — расход в отводе; Ri
— радиус центра тяжести i-го элемента отвода: r2 — радиус наружной окружности рабочего колеса; Qδi — расход, поступающий в i-й элемент отвода из рабочего колеса; Qci — расход через i-e сечение отвода; δi — угол разделения потоков
При работе насоса имеет место либо слияние, либо разделение потоков в рассматриваемых элементах. Поскольку при этом происходит изменение скоростей по величине и направлению и существует трение, то движение жидкости сопровождается гидравлическими потерями.
Гидравлические потери для выделенных элементов можно получить с помощью уравнения момента количества движения, закона сохранения энергии и уравнения неразрывности. При известных коэффициентах неравномерности параметров потока по сечению они имеют вид:
а) слияние (элемент В, рис. 6.8): выход из колеса
|
|
|
|
Q |
|
F |
|
|
2 |
|
|
Q |
2 |
F |
|
||||||
hсл = K сл[1+ |
|
δi |
|
i |
|
− |
2 1 |
− |
|
δi |
|
i |
− |
||||||||
|
|
|
|
|
|
|
|||||||||||||||
δi |
δ |
|
|
|
|
|
|
|
|
|
|
|
|
Qci |
|
Fi+1 |
|
||||
|
|
|
|
Qci |
|
Fδi |
|
|
|
|
|
||||||||||
|
Q |
|
2 |
|
F |
r 2 |
|
|
|
|
Q |
|
|
|
|
|
|||||
|
− 2 |
δi |
|
|
|
i |
|
|
|
|
cosδ |
] |
|
ci |
|
; |
|
|
(6.10) |
||
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
||||||||
|
|
|
|
|
Fδi |
Ri |
|
|
i |
|
|
|
|
|
|
|
|||||
|
Qci |
|
|
|
|
|
|
|
2gFi |
|
|
|
|||||||||
проход через i-й участок
243
|
|
|
|
|
Q |
|
|
|
|
|
|
hсл = hсл + K сл 1 |
− |
δi |
|||
|
|||||
ni |
δ |
п |
|
|
Qci |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
F |
2 |
Q |
2 |
|
F |
2 |
|
Q2 ci |
|
|
|
|
|
|
i |
|
− |
δi |
|
|
i |
|
|
|
|
; |
(6.11) |
|
Fi 1 |
|
Qci |
|
F i |
|
2gFi |
2 |
|
|
||||
|
|
+ |
|
|
|
|
δ |
|
|
|
|
|
|
|
б) разделение (элемент С, рис. 6.8): вход в колеса
|
p |
|
|
|
Q |
|
h |
= K |
p |
+ |
|
δj |
|
|
|
|||||
|
1 |
Qcj |
||||
δj |
|
δ |
|
|||
|
|
|
|
|
|
|
F |
j |
|
2 |
Q |
|
F |
j |
|
r2 |
|
|
Q2 |
||
|
|
− 2 |
δj |
|
|
|
cosδ |
|
cj |
, |
||||
F |
|
Q |
|
F |
|
|
|
|||||||
|
|
|
|
|
|
R |
|
|
j |
2gF 2 |
||||
δj |
|
cj |
|
δj |
|
|
j |
|
j |
|||||
проход через j-й участок
h |
|
= K |
|
|
Q |
F |
|
2 |
− 2 |
Q F R |
|
Q2 |
||||||||||||||||
p |
1+ |
|
|
cj+1 |
|
|
|
|
j |
|
cj+1 |
|
|
|
|
j j |
+1 |
cj , |
||||||||||
|
|
p |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
hj |
|
п |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Q |
|
F |
|
|
|
Q F |
+1 |
|
R |
|
2gF 2 |
||||||||||||||
|
|
|
|
|
|
|
cj |
|
|
j |
+1 |
|
|
cj |
|
|
|
j |
|
|
j |
j |
||||||
где |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
2πr b |
|
|
|
|
|
|
|
C |
m2i |
|
|
; |
|
|
|
|
(6.12) |
||||||
|
|
|
Fδi |
|
2 2 |
sin Arctg |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
|
Cu 2i |
|
|
|
|
|
|
|
|
|||||
δi — угол слияния или разделения потоков; |
Ri — |
радиус центра тяжести i-го сечения |
||||||||||||||||||||||||||
спирали. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В формулах принято, что коэффициенты неравномерности потока по сечению равны единице.
У элементов с малым искривлением оси можно считать:
Kδc = Kпc = Kδр = 1; Kпр = 0,4.
Посредством потери энергии при движении жидкости от выхода из i-го участка рабочего колеса до входа в напорный патрубок в виде
i |
i |
+ hвх , |
|
hi = hδi + ∑hnj + ∑hтрj |
(6.13) |
||
j=1 |
j=1 |
|
|
где hТРj — потери на трение на j-м участке; |
hвх — |
потери на разделение или слияние в |
|
элементе А. Тогда для заданного режима работы насоса параметры потока на выходе из рабочего колеса должны удовлетворять перечисленным ниже условиям.
1. Напор, создаваемый в патрубке насоса, равен напору, развиваемому i-м участком колеса с учетом гидравлических потерь в колесе hк за вычетом гидравлических потерь на протяжении от данного участка до напорного патрубка, и одинаков для всех участков:
|
|
|
N |
|
N |
|
H тi − hi |
− hк = |
|
= ∑(H тi − hi |
− hк )Qδi |
/ ∑Qδi |
(6.14) |
H |
||||||
|
|
|
i=1 |
|
i=1 |
|
2. Для выбранного режима работы насоса сумма мощностей, передаваемых жидкости по участкам, равна заданной мощности, затрачиваемой колесом:
244
N |
|
ρ ∑ H тi Qδi = Nг |
(6.15) |
i=1
3.При установившемся режиме работы насоса сумма гидравлических потерь по замкнутому контуру равна нулю:
|
∑(hпi + hтрi )+ hпA = 0 |
(6.16) |
В этих формулах hА |
— потери на проход на участке А; Н — |
напор, создаваемый насосом |
п |
|
|
в патрубке; ρ — плотность перекачиваемой среды; Nг — гидравлическая мощность колеса, известная из предварительного расчета или из обработки экспериментальных данных; Qδi
—расход среды, выходящей из i-го участка колеса.
Нетрудно видеть, что получена замкнутая система нелинейных уравнений, решение которых дает распределение параметров потока вокруг рабочего колеса. Следовательно, решив уравнения (6.11) — (6.16), можно получить необходимые данные для вычисления радиальной силы, используя уравнения (6.7) — (6.9).
Следует добавить, что в процессе решения находятся гидравлические потери в отводе, а это, в свою очередь, является самостоятельной проблемой при проектировании насосов.
Для заданного режима работы насоса задача определения оптимальной в отношении потерь геометрии отвода сводится к нахождению минимума функции вида
h = f (xi ), i = 1, 2,…, N,
где h — средние потери в отводе; хi — геометрические характеристики i-го сечения.
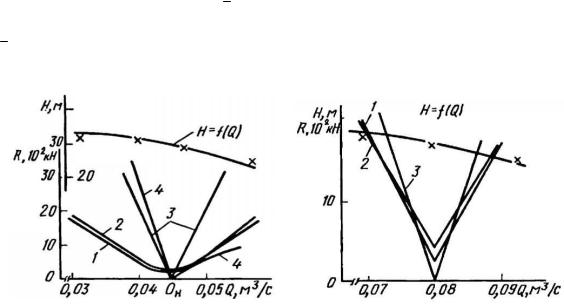
Рис. 6.9. Зависимость радиальной силы R от подачи в насосе 6К-8:
1 — экспериментальные данные; 2 — расчет по предлагаемой методике; 3 — расчет по [1, Введение] ; 4 — расчет по [7]; кривая Н = f{Q) — экспериментальные данные; символы — расчет по предлагаемой методике
Рис. 6.10. Зависимость радиальной силы R от подачи для насоса 8К-17:
1 — экспериментальные данные; 2 — расчет по предлагаемой методике; 3 — расчет по [3]; кривая Н= f(Q) — экспериментальныеданные; символы — расчетпопредлагаемойметодике
245
Решение данной задачи с использованием предложенного способа расчета не вызывает принципиальных затруднений.
Сопоставление результатов предлагаемого способа расчета радиальных сил с экспериментальными данными было проведено для насосов 6К-8 (ns = 80) и 8К-17 (ns = 170). На рис. 6.9 и 6.10 приведены зависимости R = f(Q) дли этих насосов.
Вцелях сравнения разработанного способа расчета с ранее предложенными на рис. 6.9
и6.10 приведены также зависимости, определенные по [6, 7]. Видно, что способ в целом описывает зависимость значительно точнее.
Для насосов с однозаходным спиральным отводом результаты расчета достаточно хорошо совпадают как в качественном, так и в количественном отношении с данными эксперимента. Это свидетельствует о том, что предлагаемая математическая модель правильно описывает общие закономерности движения жидкости в отводе.
Кроме расчетной зависимости на рис. 6.9, 6.10 приведены гидравлические характеристики насосов. Хорошее совпадение расчетных точек с экспериментальными кривыми также служит подтверждением правомерности данного способа расчета.
6 . 4 . 1 . СПОСОБЫ ВОЗДЕЙСТВИЯ НА РАДИАЛЬНЫЕ СИЛЫ Для уменьшения радиальных нагрузок применяются двухзаходные спиральные отводы
и т. п.
Интерес представляют некоторые способы воздействия на радиальные силы. Они в основном используются в тех случаях, когда необходимо уменьшить радиальные усилия в ГЦН в процессе их опытной отработки. Специальные устройства (рис. 6.11) позволяют создать силу, противоположную по направлению известной радиальной силе. В результате происходит полное или частичное уравновешивание радиальной нагрузки. При применении устройства противодействующая радиальная сила создается благодаря повышенному давлению на участке поверхности лабиринтного уплотнения рабочего колеса. Это достигается применением либо паза в цилиндрической стенке (рис. 6.11, а) [8], либо выступа, выполненного в виде сектора, закрепленного на корпуce (рис. 6.11, б)
[9].Расположение этих устройств соответствует направлению вектора радиальной силы.
Вустройстве, показанном на рис. 6.11, в, появление уравновешивающей силы достигается применением одного или двух радиальных ребер, расположенных в пазухах насоса. При этом ось симметрии ребер отстоит от направления обратного действия Радиальной силы на угол 60—90° против вращения колеса. Уравновешивающая сила обусловлена несимметричным обтеканием ребер: перед ними из-за торможения потока происходит повышение давления, а за ними — снижение.
246
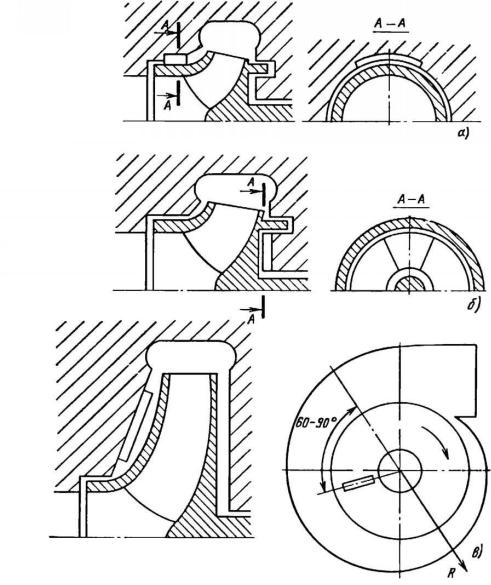
Рис. 6.11. Конструкционные схемы воздействия на радиальные силы
6 . 4 . 2 . СОСТАВЛЯЮЩИЕ РАДИАЛЬНОЙ СИЛЫ Говоря о радиальной силе, мы до сих пор подразумевали ее среднее значение за
некоторый промежуток времени в установившемся режиме работы ГЦН. Типичная запись изменения радиальной силы во времени, полученная на электромагнитном осциллографе, представлена на рис. 6.12. Из записи видно, что радиальная сила состоит из статической и динамической компонент, причем последняя имеет волновой характер и по величине вполне соизмерима с первой. Оказалось, что динамическая компонента не является циклической относительно одного оборота вала в области малых подач — от нуля до 0,5Qном, когда поток в колесе нестабилен.
247
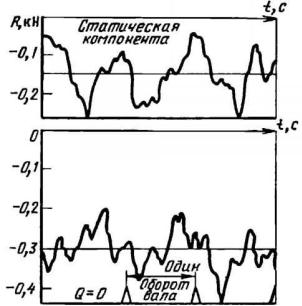
Рис. 6.12. Записимость радиальной силы R от времени t
Вдинамической компоненте можно выделить три составляющие. Первая — возникает на частоте, равной частоте вращения вала ω. Ее амплитуда, постоянная на малых подачах, возрастает с увеличением подачи. Частота второй составляющей равна произведению частоты вращения вала и числа лопастей колеса: ωz1. Она тоже хорошо обнаруживается на всех подачах. Третья составляющая имеет место на всех прочих частотах. Амплитуда ee, значительная на малых подачах, когда отсутствует цикличность радиальной силы вследствие нестабильности потока в насосе, уменьшается с возрастанием подачи и имеет минимальное значение вблизи Qном, когда поток по периферии колеса стабилен.
Волновой характер радиальной силы во многом предопределяет виброакустические характеристики ГЦН. Так, значительная вибрация наблюдается на частотах ωz1, ωz1z2. При рациональном выборе чисел z1 и z2 лопаток колеса и направляющего аппарата обеспечивается минимальное значение уровня вибрации (в частности, целесообразно выбирать z1 четным, a z2 нечетным, или наоборот). Если статическая компонента радиальной силы вызывается асимметрией отвода и подвода, то динамическая обусловлена неидентичностью каналов рабочего колеса. При этом асимметрия потока на входе и выходе из рабочего колеса также сказывается на величине динамической составляющей.
Вкачестве примера можно привести насос с ns = 110, с отводом в виде направляющего аппарата со сборной камерой, в котором обнаружена связь между эксцентриситетом в лабиринтном уплотнении рабочего колеса и радиальной силой. Причинами изменения радиальных нагрузок при изменении эксцентриситета в щели лабиринта являются перераспределение поля ркоростей на всасывании ГЦН, вызванное перераспределением
248
протечек по окружности лабиринтного уплотнения, и изменение подъемной поперечной силы в щели лабиринта.
Исследовании проводились на вертикальном насосе с осевым подводом жидкости, радиальным направляющим аппаратом и боковой сборной камерой. Число лопаток рабочего колеса zр к = = 7, число лопаток направляющего аппарата zн а = 8.
Радиальные силы измерялись при помощи специально разработанного устройства, в котором радиальные подшипники вывешивались на четырех кольцевых тензоэлементах. Предварительно проводилась тарировка устройства по радиальным нагрузкам. При этом оказалось возможным кроме значения силы определить и ее направление. Это позволило при обработке результатов измерений получать мгновенные значения нагрузок, действующих на рабочее колесо. Тензометрическая система обеспечивала погрешность измерений не более ±10%.
При обработке осциллограмм на режимах Q=(0,5÷1,4)Q ном была обнаружена четкая периодичность нагрузок, равная частоте вращения вала. Это позволило анализировать изменение силы за один оборот вала. При подачах, близких к нулевым (Q<0,5Qном), наблюдалось хаотическое изменение нагрузок, вызванное, по-видимому, возникновением срывных и помпажных явлений в колесе. Анализу подвергались режимы, в которых наблюдалась периодичность нагрузок с частотой вращения вала.
Измерения показали, что в насосе существуют значительные радиальные нагрузки, зависящие от режима работы.
Спектральный анализ осциллограмм, приведенных на рис. 6.12, позволил выделить частоты, на которых имеют место наибольшие нагрузки. Амплитуды значения нагрузок на различных частотах представлены в табл. 6.1.
Из таблицы видно, что наиболее существенными являются постоянная составляющая и переменные составляющие результирующей силы, кратные ω и 7ω, где ω — основная частота вращения вала.
Наличие периодической радиальной нагрузки, изменяющейся с частотой zω, обусловлено несимметрией потока на входе и выходе из рабочего колеса, где z — число лопаток рабочего колеса (z = 7).
|
|
|
|
|
|
|
|
|
Таблица 6.1 |
||
|
|
|
|
|
|
|
|
|
|
|
|
Подача |
|
|
|
Радиальная сила, кН |
|
|
|
|
|||
насоса, м3/ч |
|
|
|
|
|
|
|
|
|
|
|
ω |
2ω |
3ω |
4ω |
5ω |
6ω |
7ω |
8ω |
const |
|||
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
161 |
66 |
13 |
9 |
11 |
11 |
2 |
13 |
9 |
86 |
|
|
186 |
43 |
19 |
11 |
11 |
16 |
13 |
38 |
15 |
91 |
|
|
248 |
54 |
23 |
10 |
21 |
39 |
73 |
86 |
3 |
146 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
249
При анализе данных эксперимента было сделано предположение о наличии в лабиринтном уплотнении рабочего колеса эксцентриситета и о влиянии его как на постоянную, так и на переменные радиальные нагрузки, действующие на рабочее колесо.
В целях проверки высказанного предположения были проведены эксперименты при различной величине относительного эксцентриситета в нижнем лабиринтном уплотнении колеса χ =0 и χ = 0,3. Номинальный радиальный зазор в данном случае был равен 0,31 мм.
Результаты измерения радиальных сил приведены в табл. 6.2, откуда видно, что при χ = 0,3 значения постоянной и переменных составляющих радиальной силы существенно выше, чем при χ =0. Очевидно, что при χ =0 рабочее колесо работает в относительно равномерном потоке и при этом все гидравлические нагрузки малы. При χ = 0,3 появляется окружная неравномерность потока на входе рабочего колеса, следствием чего и является увеличение радиальных нагрузок.
|
|
|
|
|
|
|
|
|
Таблица 6.2 |
||
|
|
|
|
|
|
|
|
|
|
|
|
Режим работы |
|
|
|
Радиальная сила, Н |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
Rст |
|
Rω |
|
|
R7 ω |
|
||||
насоса |
|
|
|
|
|||||||
|
χ= 0 |
|
χ= 0,3 |
χ= 0 |
|
χ= 0,3 |
|
χ= 0 |
|
χ= 0,3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Qном |
31 |
|
86 |
2 |
|
55 |
|
5 |
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1,4Qном |
51 |
|
137 |
11 |
|
21 |
|
15 |
|
89 |
|
6 . 5 . О СЕВ Ы Е СИ Л Ы
При больших единичных мощностях агрегатов осевые усилия, действующие па рабочие колеса, могут достигать нескольких десятков и даже нескольких сот тонн. Поэтому определение фактических осевых усилий является весьма актуальным.
Расчет сил, действующих па боковые поверхности рабочих колес, может быть представлен в виде двух отдельных задач, каждая из которых до настоящего времени не имеет строго аналитического решения. Первая — определение полей скоростей и давлений на входе в зазоры между колесом и корпусом; вторая — расчет течения жидкости в зазорах между вращающимся колесом и кожухом при известных входных граничных условиях и геометрии зазора.
Обе задачи взаимосвязаны и могут быть решены при ряде упрощающих предположений итерационным способом. Рассматривая их независимо друг от друга, можно получить результаты, которые в дальнейшем используют для расчетов осевых усилий.
В [2] приводится следующая зависимость для определения статического давления на выходе из рабочего колеса:
250
