Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

Нижегородский Государственный Технический Университет им. Р.Е.Алексеева

Выксунский филиал

Кафедра общеобразовательных и общепрофессиональных дисциплин

Методическое пособие

к выполнению лабораторной работы №2-6

«Магнитное поле соленоида. Датчик Холла»

Для студентов всех специальностей и всех форм обучения ВФ НГТУ

г. Выкса

2009г.

Составители: В.П. Маслов, О.Д. Честнова, С.А.Ковыляев

Определение индукции магнитного поля соленоида на основе закона Био-Савара-Лапласа и с применением датчика Холла.: методическое пособие к выполнению лаб. работы №2-6 по дисциплине «Физика» для студентов всех специальностей и всех форм обучения ВФ НГТУ; сост.: В.П.Маслов и др. г.Н.Новгород, 2009. -9с.

Дана методика определения индукции магнитного поля соленоида на основе закона Био-Савара-Лапласа и с применением датчика Холла.. При написании использованы описания лабораторных работ НГТУ, МАИ, МИФИ, СФТИ и др. вузов.

Научный редактор А.А. Радионов

Редактор Э.Б. Абросимова

Подписано в печать Формат 60х48 1/16. Бумага газетная.

Печать офсетная. Усл. п. л. 0,75. Уч.-изд. л. 0,75. Тираж 200 экз. Заказ 14.

Нижегородский Государственный Технический Университет им. Р.Е.Алексеева

Типография НГТУ. 603950, ГСП-41, г. Нижний Новгород, ул. Минина, 24.

© Нижегородский государственный технический

университет им. Р.Е.Алексеева, 2009

Цель работы: ознакомиться с определением индукции магнитного поля соленоида на основе закона Био-Савара-Лапласа и с применением датчика Холла.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Закон Био-Савара-Лапласа. Вывод формулы для напряженности и индукции магнитного поля на оси кругового витка с током.

В пространстве, окружающем проводники с током, движущиеся заряды, магниты, возникает магнитное поле, которое можно обнаружить по воздействию его на другой проводник с током или магнитную стрелку. Магнитное поле в каждой точке пространства количественно может быть описано с помощью вектора напряженности магнитного поля или с помощью вектора индукции магнитного поля . В вакууме векторы и связаны соотношением:

, (1)

где μ₀ = 4π·10 ^-7 Гн/м - магнитная постоянная.

Единицы измерения и А/м и Тл соответственно. В среде с магнитной проницаемостью μ

Для вычисления напряженности и индукции магнитного поля, используют закон Био-Савара-Лапласа, согласно которому элементарная напряженность магнитного поля , создаваемая элементом проводника с током в некоторой точке пространства на расстоянии , определяется выражением:

, (2)

где – единичный вектор, направленный вдоль .

Модуль вектора:

,

где – угол между векторами и .

Для нахождения результирующей напряженности, создаваемой проводником конечных размеров, надо воспользоваться принципом суперпозиции магнитных полей и найти векторную сумму элементарных напряженностей от всех элементов проводника. Применим формулу (2) для вычисления напряженности магнитного поля на оси кругового витка с током (рис.1).

На рис.1 компонента , созданная элементом тока , согласно (2) определяется как

,

где учтено, что угол между и прямой. Из симметрии элементов витка по отношению к точке А видно, что результирующая напряженность магнитного поля направлена вдоль оси так, что , то есть

.

В правой части последней формулы все-величины, кроме , постоянны (для данной точки А), поэтому интегрирование no дает

,

или согласно рис.1

(3)

Величину можно найти по формуле (1).

Вывод формулы для напряженности и индукции магнитного поля на оси соленоида (на расстоянии z от средней точки на оси)

Пусть на единицу длины соленоида приходится n витков (рис.2), тогда участок содержит витков, которые, согласно (3), в точке А на оси создадут напряженность

. (4)

На рис.2 – длина соленоида, а - радиус витков обмотки, 0 -центральная точка на оси соленоида. ОА=z – координата точки А.

На рис. 3 отдельно изображены элементы dz, радиус-вектор и углы и . Из геометрических построений рис.2 и 3 следует:

; ; .

Подставим эти соотношения в (4) и проинтегрируем по в пределах от до :

.

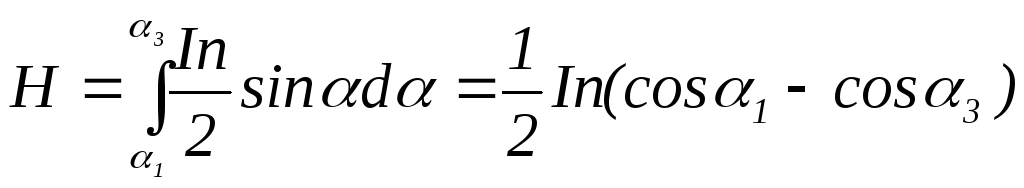Учитывая, что , получим

(5)

В случае бесконечно длинного соленоида () в центральной точке 0 ,

. (6)

Из (5) также следует, что при переходе от центра к краю полубесконечного соленоида (на краю z=0,5L, α₁=π/2, α₂→0) напряженность уменьшается вдвое:

. (7)

Индукцию, магнитного поля получим, добавив к выражениям (5), (б), (7) формулу (1). Отметим, что вывод формулы (6) для бесконечно длинного соленоида получается существенно проще на основе закона полного тока.