Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Нижегородский Государственный Технический Университет

Выксунский филиал

Кафедра ОиОПД

Определение электрических свойств

сегнетоэлектриков

Лабораторная работа № 2-13

г. Выкса

2006 г.

Составили: В.П.Маслов, И.И.Рожков, О.Д.Честнова, Р.В.Щербаков.

Дана методика осциллографического измерения параметров петли гистерезиса сегнетоэлектрика. При составлении пособия использованы описания лабораторных работ НГТУ, МАИ и других вузов.

Научный редактор А.А. Радионов.

Цель работы: изучение зависимости диэлектрической проницаемости сегнетоэлектрика от напряженности электрического поля, определение остаточной поляризации и коэрцитивной силы путем наблюдения петли гистерезиса при различных напряжениях питания.

ВВЕДЕНИЕ

В составе атомов и молекул имеются положительно заряженные ядра и отрицательно заряженные электроны. В целом молекула нейтральна, но мо­жет обладать электрическим дипольным моментом

,

где q – абсолютная величина суммарного заряда одного знака, - вектор, про веденный из «центра тяжести» отрицательных зарядов - электронов в «центр тяжести» положительных зарядов - ядер («плечо диполя»). Молекулы могут обладать дипольным моментом - при отсутствии внешнего электрического поля (полярные молекулы) или только при наличии такого поля (неполярные молекулы). Явление поляризации диэлектрика заключается в том, что под действием внешнего электрического поля суммарный электрический момент молекул диэлектрика становится отличным от нуля. Количественной характеристикой поляризации диэлектрика служит вектор поляризации (или вектор поляризованности), равный дипольному моменту единицы объема диэлектрика

.

Для описания электрического поля в диэлектриках, кроме напряженности и поляризации используют вектор электрического смещения (или просто вектор ). Заполнение всего свободного пространства между заряженными телами однородным диэлектриком приводит к тому, что напряженность электрического поля и сила Кулона в любой точке пространства уменьшаются в ε раз. Величина ε называется диэлектрической проницаемостью диэлектрика. Примером может служить заряженный плоский воздушный конденсатор, отключенный от источника напряжения, если его погружают в сосуд с трансформаторным маслом. Новая напряженность поля в этом диэлектрике будет равна

.

Отношение - это напряженность поля до помещения заряженного тела в диэлектрик. Связь между векторами , и можно записать также в виде

(1)

или в виде

(2)

где е - диэлектрическая проницаемость; ε₀ = 8,85- 10^-12 Ф/м – электрическая постоянная. Измеряются величины D и Р в Кл/м².

Существует особая группа кристаллических диэлектриков - сегнетоэлектрики - к которым, например, относится титанат бария ВаТiО₃. Главное их отличие состоит в том, что они могут обладать ненулевой поляризацией даже в отсутствие внешнего электрического поля. Стержень из такого вещества создает вокруг себя электрическое поле (так же, как постоянный магнит создает вокруг себя магнитное поле).

Другие характерные свойства сегнетоэлектриков состоят в следующем. В то время, как обычные диэлектрики имеют величину ε, равную нескольким единицам (для слюды ε = 7, для керамики - ε - 10, для полиэтилена - ε = 2,2), то у сегнетоэлектриков величина ε достигает значений, равных десяткам тысяч.

Зависимость от (а также от ) не является линейной (см. ветвь 1 кривой на графике рис. 1). Следовательно, диэлектрическая проницаемость оказывается зависящей от напряженности поля. В случае титаната бария с ростом напряженности Е от нуля до величины около 500 В/мм значение ε растет до величины порядка 6000 - 7000, а затем падает.

Если напряженность электрического поля менять во времени циклически, например по синусоидальному закону, то зависимость от изображается кривой, называемой петлей гистерезиса (рис. 1). При первоначальном включении поля растет в соответствии с ветвью 1 кривой. Уменьшение с уменьшением поля Е происходит по ветви 2. При обращении Е в нуль вещество сохраняет значение поляризацией Р_ост, называемое остаточной поляризованностью (или остаточной поляризацией). Как следует из уравнения (1), при Е=0 имеет место равенство D = Р, значит, значение Р_ост определяется точкой пересечения ветви 2 и оси D, в которой D_ост = P_ост Только прикладывая противоположно направленное поле с отрицательной напряженностью -Ек , смещение D можно сделать равным нулю (рис. 1). Это значение напряженно­сти электрического поля Е_к называется коэрцитивной силой. Дальнейшее уве­личение отрицательных значений Е приводит к тому, что величина D становится отрицательной. Если снова изменять Е в сторону положительных значений, то получается ветвь 3 петли гистерезиса.

Смысл слова «гистерезис» (в переводе – «запаздывание») состоит в том, что в точке D_OCT напряженность электрического поля уже нулевая, а значение D еще не достигает нулевых значений. Снижение значения D до нуля происходит с запаздыванием при значении Е = -Ек.

Если максимальное значение напряженности Е таково, что поляризация достигает насыщения, то получается петля, называемая предельным циклом. Если же при максимальной напряженности Е насыщение не достигается, то получается так называемая петля частного цикла. Насыщение титаната бария происходит при Е_т>2000 В/мм. В данной работе Е_т меньше этого значения и измерения проводятся на частном цикле.

Существует критическая температура, называемая точкой Кюри, выше которой сегнетоэлектрические свойства исчезают и кристалл становится обычным диэлектриком. Для титаната бария эта температура равна 120 °С.

С молекулярной точки зрения особые свойства сегнетоэлектриков объясняются следующим образом. Атомы сегнетоэлектрика объединяются в отдельные группы, каждая из которых занимает область размером ~ 1 мкм. Эти области называются доменами. В пределах домена дипольные моменты атомов параллельны друг другу, однако направления поляризации отдельных доменов различны по направлению и результирующее значение электрического момента всего сегнетоэлектрика близко к нулю.

Под влиянием внешнего электрического поля происходит смещение доменных стенок, причем увеличиваются размеры тех доменов, поляризация которых направлена вдоль и, кроме того, происходит поворот доменов, приближающий их к положению, в котором вектор поляризации параллелен направлению внешнего электрического поля. При уменьшении поля происходит обратный процесс. Явление гистерезиса (запаздывания) связано с тем, что перестройка доменов сопровождается потерей энергии и требуется обратная «сила» Е_к, чтобы вернуть домены в исходное состояние.

Сегнетоэлектрики применяют для изготовления конденсаторов большой емкости (так как ε велико) и варикондов - конденсаторов, емкость которых зависит от приложенного напряжения. Недостаток таких конденсаторов - ограниченный диапазон рабочих частот, температур, высокие значения диэлек­трических потерь.

Между колебаниями векторов и существует разность фаз δ. Потери энергии оцениваются величиной tgδ, называемой тангенсом угла диэлектрических потерь.

где ΔW- уменьшение объемной плотности энергии за один цикл;

W- объемная плотность энергии электрического поля в сегнетоэлектрике.

Величина диэлектрических потерь в единице объема за один цикл ΔW и объемная плотность энергии W равны соответственно:

,

.

А тангенс угла диэлектрических потерь равен

(3).

Здесь Е₀ – амплитуда напряженности электрического поля, D₀ – амплитуда электрического смещения.

Методика измерений и вывод расчетных формул

На вертикально отклоняющие пластины осциллографа подается напряжение U* с конденсатора С₂, которое пропорционально заряду этого конденсатора:

(4)

Т. к. Q₂=Q₁=σ₁S₁=D₁S₁, то из (4) получим

, (5)

Где D₁, - величина электрического смещения; S₁ - площадь пластины конденсатора, σ₁- поверхностная плотность заряда на пластинах конденсатора С₁,

Следовательно, на вертикально отклоняющие пластины осциллографа подается напряжение U*, пропорциональное величине D₁ в сегнетоэлектрике. Величина U* может быть определена, если известен коэффициент отклонения электронного луча по вертикали b₂ и величина отклонения у

U*=b₂y. (6)

Тогда из формул (5) и (6) получим

(7)

На горизонтально отклоняющие пластины подается напряжение Ux с емкостного делителя С₁ и C₂. Т.к. С₁<<C₂, то

U_x=U_C1+U_C2yU_C2=E₁h_1, (8)

Где Е, - напряженность электрического поля в сегнетоэлектрике, h₁ - толщина сегнетоэлектрика

Таким образом, на пластины «х» подается напряжение Ux, пропорциональное напряженности электрического поля в сегнетоэлектрике. Величина Ux может быть определена, если известен коэффициент отклонения луча по горизонтали b₁, и величина отклонения х.

Ux=b₁x (9)

Тогда из (8) и (9) найдем

(10)

Таким образом, на горизонтально и вертикально отклоняющие пластины одновременно подаются напряжения пропорциональные соответственно напряженности электрического поля Е и электрическому смещению D, в результате чего на экране осциллографа наблюдается петля гистерезиса Подставляя (7) и (10) в выражение (3), получим:

, (11)

где S - площадь петли гистерезиса в координатах ху, х_о, у_о – координаты вершины петли гистерезиса.

Основная кривая поляризации ОА является геометрическим местом точек вершины петель» частных циклов. Тогда, определив значения Е и D вершин частных циклов из (2), (7), и (10) найдем

(12)

Принципиальная электрическая схема

Указания по технике безопасности

1. Приборы питаются от сети 220 В. Включение в сеть приборов должно проводиться только в присутствии лаборанта или преподавателя.

2. Все корпусные клеммы должны быть надежно заземлены (для заземления должен применяться провод без изоляции).

3. во время проведения эксперимента запрещается прикасаться ко всем токоведущим частям установки (клеммы, соединительные провода и т.д.).

4. Запрещается работать в помещении одному.

5. Запрещается оставлять установку включенной.

Экспериментальная часть

Задание 1. Определение тангенса угла диэлектрических потерь.

1. Соберите схему установки в соответствии с рис. 3.

2. Подготовьте осциллограф к работе (в режиме наблюдения фигур Лиссажу).

3. Включите осциллограф и источник питания.

4. Получить максимальную петлю гистерезиса.

5. Скопировать на кальку петлю гистерезиса.

6. Измерить координаты х₀ и у₀ вершины петли гистерезиса.

7. Совместив кальку с миллиметровой бумагой, определить площадь петли гистерезиса S.

8. По формуле (11) вычислить тангенс угла диэлектрических потерь.

Задание 2. Определение остаточного смещения D_ост и коэрцитивной силы Е_к.

1. Совместить максимальную петлю гистерезиса с координатными осями.

2. Записать величины коэффициентов отклонения по горизонтали b₁ и вертикали b₂ и их погрешности.

3. Рассчитать остаточное смещение по формуле (7) и коэрцитивную силу по формуле (10). параметры экспериментальной установки: h= 0,45 мм – толщина сегнетоэлектрика; S=4,9 см² – площадь пластин; b1=2 В/дел; b2=5В/дел; Δb1=0,5В/дел ;Δb2=0,5В/дел.

4. Измерить величину у_ост при х=0.

5. Измерить величину (-х_к) и (х_к) при у=0.

6. Определить среднее значение х_{к ср} по формуле

.

7. По формулам (7) и (10) рассчитать остаточное смещение и коэрцитивную силу.

Задание 3. Определение диэлектрической проницаемости сегнетоэлектрика.

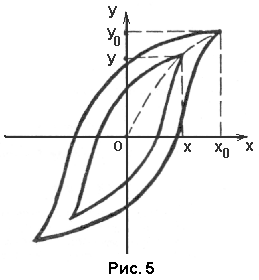
1. Получить максимальную петлю гистерезиса и измерить координаты ее вершины х₀ и у₀.

2. Изменяя напряжение на генераторе, получить четыре частных цикла и измерить координаты х₀ и у₀ их вершин.

3. Определить диэлектрическую проницаемость сегнетоэлектрика, по формуле (10).

4. По формуле (12) рассчитать относительную диэлектрическую проницаемость.

5. По рассчитанным данным построить зависимость ε = f(E).

6. Найти погрешность определения ΔЕ.

или

.

7. Найти погрешность определения Δε (ε₀=8,85·10^-12 Ф/м).

или

.

11