Федеральное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Нижегородский Государственный Технический Университет

Выксунский филиал

Кафедра общей физики

Лабораторная работа ФПТ1-4.

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ВЗАИМНОЙ ДИФФУЗИИ ВОЗДУХА И ВОДЯНОГО ПАРА.

г. Выкса

2006 г.

Введение.

Физические основы явлений переноса.

Явления переноса обусловлены хаотическим движением молекул газа, которые, переходя из одних точек пространства в другие, переносят присущие им количество движения, энергию и массу. К таким явлениям относятся: внутреннее трение или вязкость (обусловленная переносом количества движения), теплопроводность (обусловленная переносом энергии) и диффузия (обусловленная переносом массы вещества).

Явления переноса возникают при нарушении равновесия в системе, носят необратимый характер и стремятся привести систему в равновесное состояние. Они вызваны неодинаковыми значениями какой – либо величины в пространстве. Так, внутреннее трение вызвано разницей скоростей течения слоев газа, теплопроводность – разностью температур слоев, диффузия – переменной концентрацией частиц вещества.

Н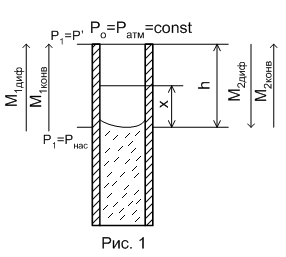 еоднородность в пространстве значений величины может быть задана с помощью ее градиента – вектора, характеризующего изменение этой величины при перемещении на единичную длину и направленного в сторону наиболее быстрого ее возрастания. При записи уравнения переноса будем полагать, что изменение этой величины происходит только вдоль одной из координат, например, вдоль оси ОХ.

Диффузия. Это процесс выравнивания концентраций газов, который сопровождается переносом массы соответствующего компонента газа из области с большей в область с меньшей концентрацией. Масса компонента газа, переносимая вследствие диффузии через поверхность площадью S, перпендикулярную оси ОХ, за время τ, определяется законом Фика:

. (1)

Здесь - градиент плотности компонента газа (ρ – плотность компонента газа, ρ=m₀n, где m₀ – масса молекулы компонента газа, n – концентрация молекул компонента газа); D – коэффициент диффузии.

Коэффициент диффузии численно равен массе данного компонента, переносимой через единицу площади поверхности за единицу времени при единичном градиенте плотности. В СИ единицей коэффициента диффузии является квадратный метр на секунду (м²/с).

Знак минус в уравнении (1) обусловлен тем, что перенос массы всегда осуществляется в сторону уменьшения величин, неоднородностью которых он вызван. Градиент же по определению всегда направлен в сторону увеличения соответствующей величины.

Определение коэффициента взаимной диффузии воздуха и водяного пара.

Цель работы: изучение диффузии как одного из явлений переноса. Определение коэффициента взаимной диффузии воздуха и водяного пара по скорости испарения жидкости из капилляра.

Методика измерений.

Наиболее распространенным методом определения коэффициента взаимной диффузии воздуха и водяного пара является метод, основанный на измерении скорости испарения жидкости, частично заполняющей узкую трубку постоянного сечения S, в атмосферный воздух (рис. 1).

Пусть все величины, характеризующие состояние водяного пара, имеют индекс «I», а величины, характеризующие состояние воздуха – индекс «2».

На границе с жидкостью (х=0) парциальное давление пара р₁ равно давлению насыщенного пара р_нас при температуре опыта. внутри трубки давление водяного пара изменяется от р_нас до давления р′ на срезе трубки, соответствующего влажности воздуха в лаборатории, т. е. существует градиент парциального давления пара , вследствие чего в трубке возникает диффузионный поток М_1диф пара, направленный вверх (рис. 1).

На основе закона Фика (1) получим выражение, связывающее массу пара, переносимую через площадь поперечного сечения трубки за одну секунду, с градиентом давления водяного пара. Плотность пара можно выразить через его парциальное давление, используя основное уравнение молекулярно – кинетической теории:

.

, (2)

где m₀₁ – масса молекулы пара; М₁ – молярная масса пара.

Используя соотношение (2), выражение закона Фика (1) для диффузии пара можно представить в виде:

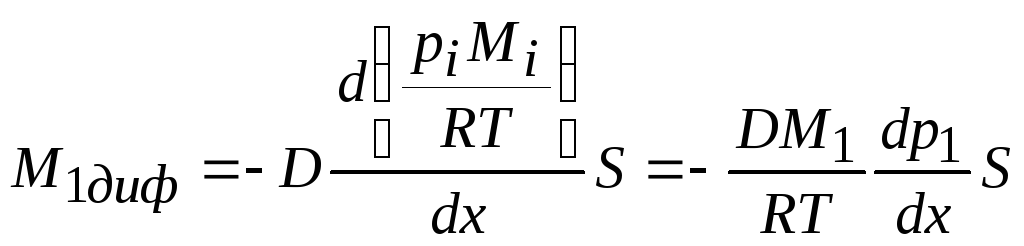. (3)

Так как в любом сечении капилляра общее давление р₀, равное сумме парциальных давлений пара р₁ и воздуха р₂, постоянно и соответствует атмосферному давлению:

, (5)

то (6)

Уравнение (6) указывает на наличие в трубке градиента парциального давления воздуха с обратным знаком. Вследствие этого в трубке при x>0 существует диффузионный поток воздуха, направленный вниз и переносящий в соответствии с (3) за одну секунду массу воздуха:

, (7)

где М₂ – молярная масса воздуха.

Поверхность жидкости непроницаема для воздуха, поэтому для компенсации приходящего воздушного диффузионного потока в капилляре должен существовать общий конвективный поток смеси, направленный вверх, с которым за одну секунду переносится масса М_конв=М_1конв+М_2конв. Массу компонента газа, переносимую за одну секунду с конвективным потоком смеси, можно представить в виде:

, (8)

или, с учетом формулы (2) в виде:

, (9)

где u – скорость конвективного потока смеси.

Соответственно масса водяного пара, переносимая за одну секунду диффузионным и конвективным потоками через площадь поперечного сечения капилляра, запишется следующим образом:

. (10)

Поскольку масса воздуха, переносимая диффузионным потоком вниз [см (7)], равна массе воздуха, переносимой конвективным потоком вверх [см (9)], то:

. (11)

Из (11) находим скорость конвективного потока смеси:

. (12)

Или с учетом соотношений (7) и (8):

. (13)

Подставляя (13) в (10)получаем следующее выражение для массы пара, переносимой за одну секунду через площадь поперечного сечения капилляра:

. (14)

Массу пара М₁ можно выразить через скорость понижения уровня жидкости в капилляре:

, (15)

где ρ_ж – плотность жидкости; Δр – понижение уровня жидкости за время Δτ.

Выражение (15) с учетом (14) запишется в виде:

. (16)

Уравнение (16) можно решить методом разделения переменных:

.

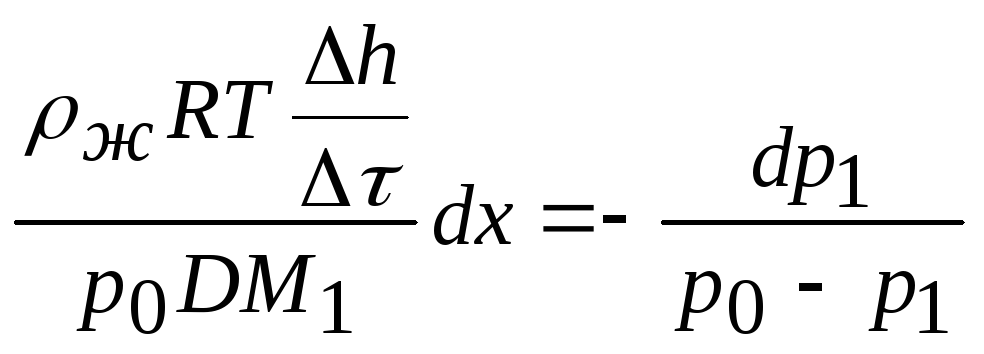Интегрируя и подставляя пределы для х от 0 до h, а для р₁ от р_нас до р′, т. е. давления, соответствующего влажности воздуха в помещении лаборатории, получаем:

.

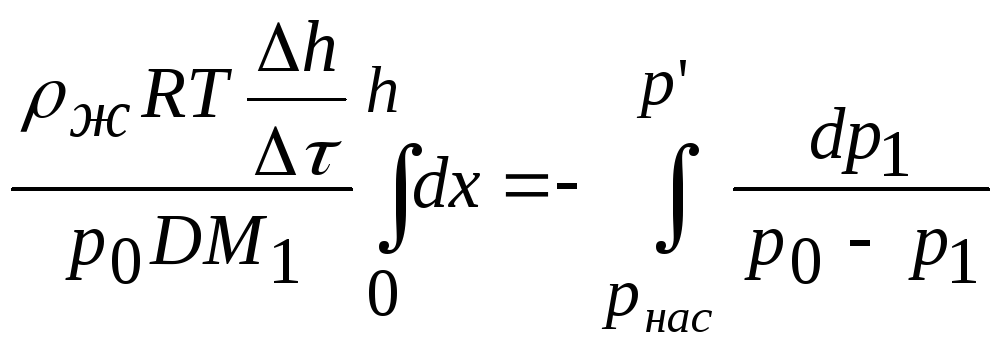Откуда

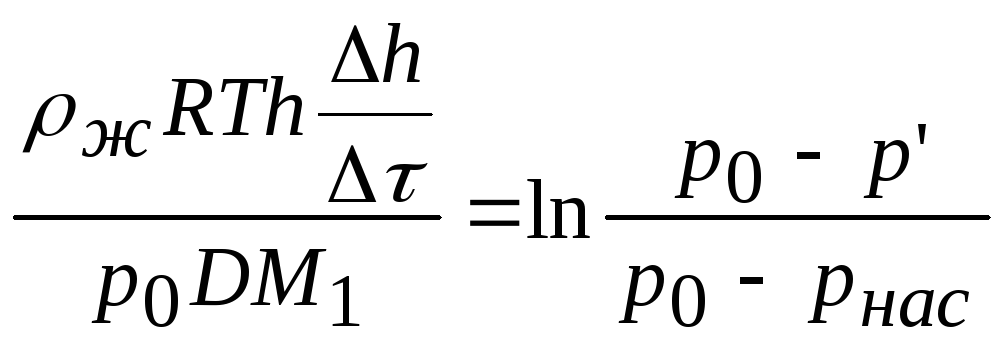. (17)

Из уравнения (17) находим расчетную формулу для определения коэффициента взаимной диффузии воздуха и водяного пара:

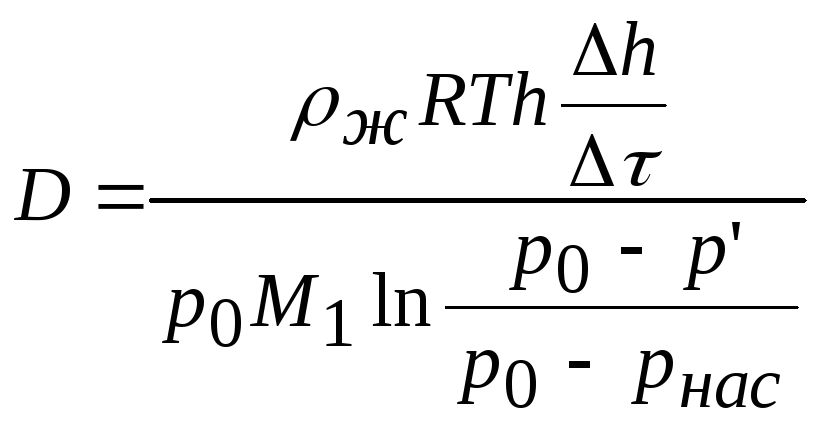. (18)