ФИЗИКА 1 семестр / Отчёты 1 семестр / Методички 1 семестр / ФПТ1-3 Теплопроводность воздуха

01Федер00000000000альное агентство по образованию

Государственное образовательное учреждение высшего профессионального образования

Нижегородский Государственный Технический Университет

Выксунский филиал

Кафедра общеобразовательных и общепрофессиональных дисциплин

Лабораторная работа ФПТ1-3.

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА ТЕПЛОПРОВОДНОСТИ ВОЗДУХА МЕТОДОМ НАГРЕТОЙ НИТИ.

г. Выкса

2006 г.

Составили: В.П.Маслов, И.И.Рожков, О.Д.Честнова, Р.В.Щербаков.

В работе изучается теплопроводность как одно из явлений переноса в газе. Дана методика определения коэффициента теплопроводности воздуха методом нагретой нити, описание установки и порядок работы на ней. При написании использованы описания лабораторных работ НГТУ, МАИ, МИФИ, СФТИ и др. вузов.

Научный редактор А.А. Радионов

Введение.

Физические основы явлений переноса.

Явления переноса обусловлены хаотическим движением молекул газа, которые, переходя из одних точек пространства в другие, переносят присущие им количество движения, энергию и массу. К таким явлениям относятся: внутреннее трение или вязкость (обусловленная переносом количества движения), теплопроводность (обусловленная переносом энергии) и диффузия (обусловленная переносом массы вещества).

Явления переноса возникают при нарушении равновесия в системе, носят необратимый характер и стремятся привести систему в равновесное состояние. Они вызваны неодинаковыми значениями какой – либо величины в пространстве. Так, внутреннее трение вызвано разницей скоростей течения слоев газа, теплопроводность – разностью температур слоев, диффузия – переменной концентрацией частиц вещества.

Неоднородность в пространстве значений величины может быть задана с помощью ее градиента – вектора, характеризующего изменение этой величины при перемещении на единичную длину и направленного в сторону наиболее быстрого ее возрастания. При записи уравнения переноса будем полагать, что изменение этой величины происходит только вдоль одной из координат, например, вдоль оси ОХ.

Теплопроводность. Это процесс передачи теплоты от более нагретого слоя газа к менее нагретому за счет хаотического теплового движения молекул. Он не сопровождается макроскопическим движением среды. Количество теплоты Q, переданное вследствие теплопроводности через поверхность площадью S, перпендикулярную оси ОХ, за время τ, определяется законом Фурье:

, (1)

где - градиент температуры; æ – коэффициент теплопроводности.

Коэффициент теплопроводности численно равен количеству теплоты, проходящему через единицу площади поверхности за единицу времени при единичном градиенте температуры. В СИ единицей коэффициента теплопроводности является ватт на метр-кельвин (Вт/(м·К)).

Определение коэффициента теплопроводности воздуха методом нагретой нити.

Цель работы: изучение теплопроводности как одного из явлений переноса в газах.

Методика измерений.

Воздухом заполняют пространство между двумя коаксиальными цилиндрами, причем внутренним цилиндром может быть просто тонкая проволока, которая является одновременно и нагревателем, и термометром сопротивления. Если через проволоку пропускать ток, а на внешней стенке наружного цилиндра поддерживать постоянную температуру, более низкую, чем температура нагревателя, то в кольцевом слое газа возникнет радиальный поток теплоты, направленный от проволоки к стенке.

Распространение теплоты в газах происходит тремя способами: тепловым излучением (перенос энергии электромагнитными волнами), конвекцией (перенос энергии за счет перемещения слоев газа в пространстве из областей с высокой температурой в области с низкой температурой) и теплопроводностью.

Однако поток лучистой энергии при невысоких температурах и малом диаметре нагревателя составляет незначительную долю переносимого количества теплоты, а конвекция устраняется подбором диаметра наружной трубки и ее вертикальным расположением в установке. Поэтому с достаточной точностью можно полагать, что передача теплоты от нагревателя к наружной трубке будет осуществляться только за счет теплопроводности газа.

Количество теплоты, прошедшее за одну секунду через цилиндрический слой газа, можно определить с помощью закона Фурье. Применим уравнение (1) к задаче с осевой симметрией, т. е. рассмотрим два длинных коаксиальных цилиндра, пространство между которыми заполнено газом, коэффициент теплопроводности æ которого необходимо измерить. На рис. 1 показано поперечное сечение этих цилиндров. В качестве внутреннего цилиндра служит натянутая металлическая нить. Температуры поверхностей и радиусы внешнего и внутреннего цилиндров соответственно обозначим через T₁, r₁ и T₂ r₂.

П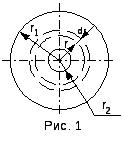ри атмосферном давлении температура слоя газа, прилегающего к стенкам, равна температуре стенок. Следовательно, температура слоя газа, прилегающего к нити, соответствует Т₂, а прилегающего к стенкам цилиндра – Т₁.

Выделим внутри газа кольцевой слой радиусом r, толщиной dr и длиной L. По закону Фурье (1) тепловой поток Q, т. е. количество теплоты, проходящее через этот слой за одну секунду, можно записать в виде:

. (2)

Это уравнение можно решить методом разделения переменных:

. (3)

Полагая æ=const в исследуемом диапазоне температур и интегрируя обе части уравнения (2), получаем:

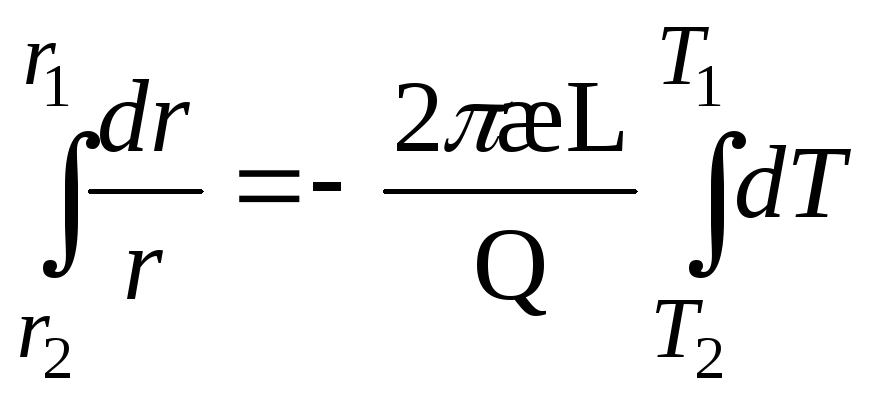. (4)

Откуда:

. (5)

Из уравнения (5) находим формулу для определения коэффициента теплопроводности:

. (6)

Здесь æ – коэффициент теплопроводности исследуемого газа, отнесенный к средней температуре этого газа; ΔТ – разность температур в слое газа, ΔТ=Т₂-Т₁.

Таким образом, для определения коэффициента теплопроводности необходимо заранее знать разность температур в слое газа и величину теплового потока Q.

Разность температур ΔТ в слое газа можно найти косвенным методом, измеряя электрическое сопротивление нити. Запишем формулы для определения сопротивлений нити при двух значениях температур:

(7)

где R₀ – сопротивление нити при t=0 ⁰С; α – температурный коэффициент материала проволоки.

Исключив из двух уравнений (7) R₀, найдем:

, (8)

где ΔR_H=R_H2-R_H1.

Следовательно, для определения разности температур в слое газа необходимо измерить температуру t₁ стенки наружного цилиндра и сопротивление нити при температуре t₁ и некоторой более высокой температуре t₂.

После установления стационарного режима, при котором разность температур в слое газа не меняется со временем, тепловой поток можно принять равным мощности электрического тока в нити:

. (9)

Подставляя (9) в (6), получаем:

. (10)

Здесь D и d – диаметры внешнего цилиндра и нити; ΔT, I_H – разность температур, определяем по формуле (8), и соответствующий ей ток в нити.

Экспериментальная установка.

Для определения коэффициента теплопроводности воздуха предназначена экспериментальная установка ФПТ1-3, общий вид которой приведен на рис. 2.

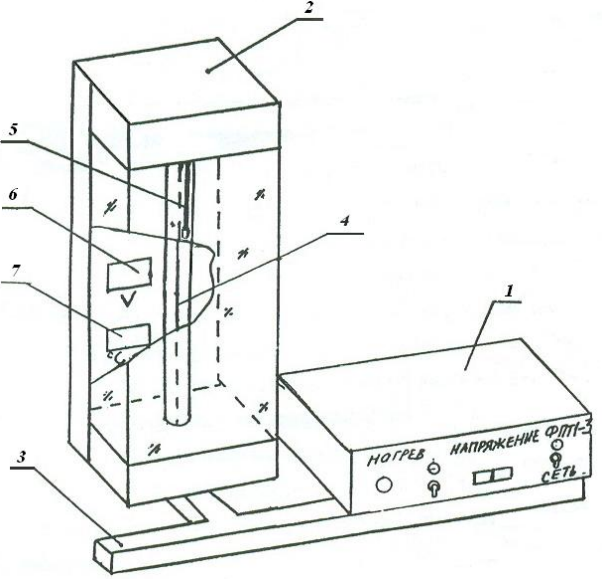
Рабочий элемент 2 состоит из стеклянной трубки, заполненной воздухом, по оси которой натянута тонкая вольфрамовая проволока 4. В течение эксперимента температура трубки поддерживается постоянной, что обеспечивается принудительной циркуляцией воздуха с помощью вентилятора между трубкой и кожухом рабочего элемента. Для измерения температуры трубки предназначен полупроводниковый термометр 5.

Температура нити тем выше, чем больше протекающий по ней ток. С повышением температуры меняется сопротивление нити, измеряемое методом сравнения падений напряжений на нити и на эталонном резисторе.

Разность температур нити и трубки определяется по формуле:

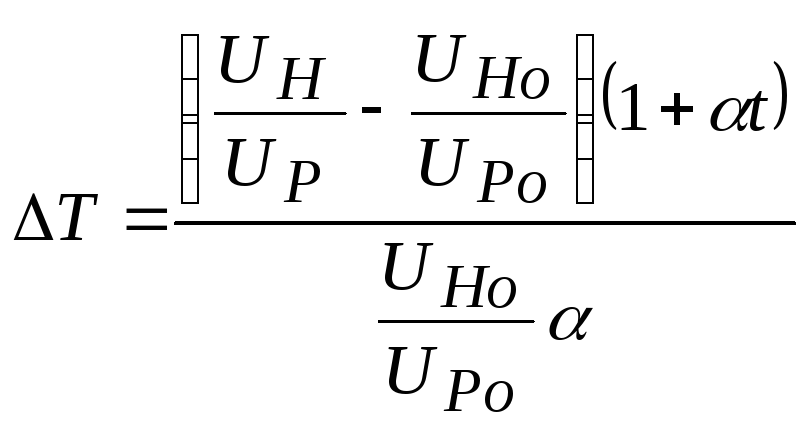, (11)

где U_H – падение напряжения на нити в нагретом состоянии; U_Ho – падение напряжения на нити при температуре окружающего воздуха (при рабочем токе не более 10 мА); U_P - падение напряжения на эталонном резисторе при нагреве нити; U_Po – падение напряжения на эталонном резисторе при температуре окружающего воздуха; α – температурный коэффициент сопротивления; t – температура воздуха.

Процесс теплопередачи путем теплопроводности от нити к окружающей среде описывается уравнением (10). Геометрические размеры рабочего элемента: диаметр трубки D, диаметр нити d, длина трубки L, - а также температурный коэффициент сопротивления материала нити α указаны на лицевой панели установки.

В установке ФПТ1-3 тепловой поток создается путем нагрева нити постоянным током и определяется по формуле:

, (12)

где U_H – падение напряжения на нити; U_P – падение напряжения на эталонном резисторе; R_P – сопротивление эталонного резистора – 41,5 Ом.

Разность температур нити и трубки:

. (13)

Порядок выполнения работы.

1. Включить тумблер ВКЛ в модуле питания СЕТЬ.

2. Нажать кнопку U_Р (режим измерения падения напряжения на эталонном резисторе).

3. Установить рукояткой НАГРЕВ напряжение U_P не более 0,060 В (негреющий ток).

4. Нажать кнопку U_H (режим измерения падения напряжения на нити) и зарегистрировать показания цифрового индикатора.

5. Рассчитать тепловой поток по формуле (12).

6. Нажать кнопку U_P и установить рукояткой НАГРЕВ напряжение U_P в диапазоне 0,3 – 1,5 В.

7. Выждать минуту для стабилизации теплового режима и определить падение напряжения на нити U_H нажатием кнопки U_H.

8. После измерения вывести ручку нагрев в крайнее левое положение.

9. Рассчитать разность температур по формуле (13) и определить коэффициент теплопроводности по формуле (10).

Контрольные вопросы.

1. Назовите возможные способы передачи тепла.

2. В чем заключается метод нагретой нити, служащий для определения коэффициента теплопроводности газов?

3. Выведите расчетную формулу для определения коэффициента теплопроводности методом нагретой нити.

4. Как оценить среднюю длину свободного пробега и эффективный диаметр молекул газа, используя явление теплопроводности?

Литература:

1. Детлаф А.А., Яворский Б.М. Курс физики. Москва ACADEMA 2003 год. С.

2. Сивухин Д.В. Общий курс физики. Т.3 Москва Астрель-АСТ. 2002 год. С. .

3. Трофимова Т.И. Курс физики. Москва ACADEMA 2004 год

С.

10