ФИЗИКА 1 семестр / Отчёты 1 семестр / Маятник Максвелла

Нижегородский Государственный Технический Университет

Выксунский Филиал

Лабораторная работа №1-4

по общей физике

Маятник Максвелла

Выполнила:

Герасимова Е. Н.

ПТК-09

Проверил:

Маслов В.П.

2009г.

1. Цель работы.

Определение момента инерции маятника Максвелла.

2.Краткие сведения из теории

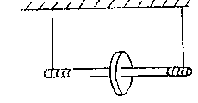
Действие прибора основано на одном из основных законов механи­ки - законе сохранения механической анергии: полная механическая анергия системы, на которую действуют только консервативные силы, постоянна. Маятник Максвелла представляет собой твердое тело, наса­женное на ось. Ось подвешена на двух накручивающихся на нее нитях (рис.1). Под действием силы тяжести маятник совершает колебания в вертикальном направлении и вместе с тем крутильные колебания во­круг своей оси. Пренебрегая силами трения, систему можно считать консервативной. потенциальной анергии. При освобождении маятника он начинает движение под действием силы тяжести: поступательное вниз и вращательное вокруг своей оси. При этом потенциальная энер­гия переходит в кинетическую. Опустившись в крайнее нижнее положе­ние, маятник будет по инерции вращаться в том же направлении, нити намотаются на ось и маятник поднимется. Так происходят колебания маятника.

Рисунок 1

Напишем уравнения движе­ния маятника. При поступательном движении маятника по вто­рому закону Ньютона с учетом действующих ни маятник сил можно написать

,

где m - масса маятника, g -ускорение силы тяжести, a - ускорение поступательного движения центра масс маятника,

Т- сила натяжения одной нити,

Проектируя это уравнение, получим

ma = mg - 2T . (1)

Для вращательного движения маятника запишем основной закон динами­ки вращательного движения для абсолютно твердого тела:

, где J- момент инерции маятника относительно его оси вращения,  - угловое ускорение маятника, М - результирующий момент внешних сил относительно оси вращения.

Поскольку момент силы тяжести относительно оси вращения равен нулю,

, (2)

где r - радиус оси. Так как и из (1) 2Т = m(g - a), можем написать:

,

а после преобразований

.

Ускорение а может быть получено по измеренному времени движения и проходимому маятником расстоянию h из уравнения равноускоренного движения без начальной скорости:

. Тогда

И если подставить диаметр оси D, получим основную расчетную формулу

. (3)

3.Описание экспериментальной установки

Схема лабораторного стенда изображена на рис. 1. Основным элементом стенда является диск 1, через центр которого проходит ось 2. На эту ось наматываются две симметрично расположенные нити З. В исходном положении (показано пунктиром на рис. 1) диск удерживается электромагнитами 4. При отключении электромагнитов диск начинает двигаться вниз с одновременным раскручиванием нитей.

Сложное движение диска можно представить как наложение двух независимых движений — поступательного и вращательного. Расстояние, проходимое центром инерции диска за счёт поступательного движения, отсчитывается по вертикальной шкале 5. Отсчёт времени поступательного движения производится по миллисекундомеру 6, на который подаётся сигнал от фотодатчика 7 в тот момент, когда край опускающегося диска пересекает световой луч фотодатчика.

При необходимости изменить общую двину пути, проходимого диском при поступательном движении, регулируют длину нитей при помощи винта 8. При этом платформу 9 с фотодатчиком также соответственно перемещают, освобождая винт 10, так, чтобы опускающийся диск пересекал световой луч, но не касался при этом самой платформы фотодатчика.

Величину ускорения поступательного движения диска можно изменять, добавляя на диск сменные кольца 11 .

m_в =(0,0500,003)кг

m_д =(0,0500,003)кг

m_к1 =(0,1580,003)кг

m_к2 =(0,3700,003)кг

m_к2 =(0,6700,003)кг

4.Исходные данные

Таблица №1

№ опыта	mд, кг	mв, кг	mк, кг	r,м	R1,м	R2,м	h,м	t, с					<t>,с
								1	2	3	4	5
1.1	0,05	0,05	0,158	0,0099	0,03	0,035	0,05	0,30	0,40	0,32	0,35	0,40	0,35
2	0,05	0,05	0,370	0,0099	0,03	0,040	0,05	0,27	0,26	0,32	0,25	0,28	0,28
3	0,05	0,05	0,670	0,0099	0,03	0,0475	0,05	0,25	0,23	0,26	0,20	0,23	0,235
2.1	0,05	0,05	0,158	0,0099	0,03	0,035	0,10	0,52	0,48	0,53	0,50	0,49	0,50
2	0,05	0,05	0,370	0,0099	0,03	0,040	0,10	0,40	0,37	0,38	0,41	0,42	0,39
3	0,05	0,05	0,670	0,0099	0,03	0,0475	0,10	0,33	0,31	0,37	0,32	0,34	0,33
3.1	0,05	0,05	0,158	0,0099	0,03	0,035	0,15	0,62	0,61	0,64	0,58	0,63	0,61
2	0,05	0,05	0,370	0,0099	0,03	0,040	0,15	0,50	0,46	0,51	0,47	0,48	0,48
3	0,05	0,05	0,670	0,0099	0,03	0,0475	0,15	0,41	0,42	0,38	0,43	0,39	0,406

где m_в=m_д - масса вала и диска,

m_к - масса колец,

r – радиус вала,

R₁ – внутренний радиус колец,

R₂ - внешний радиус колец,

h – высота подъема вала.

5.Расчеты:

1. Рассчитаем экспериментально момент инерции маятника Максвелла по формуле:

где m₁=m_в+m_д+m_кI=0,05+0,05+0,158=0,258 кг

m₂=m_в+m_д+m_кII=0,05+0,05+0,370=0,470 кг

m₃=m_в+m_д+m_кIII=0,05+0,05+0,670=0,770 кг

Таблица№2

№ опыта	mк ,кг	J, кг м2
1	0,158	0,00028 0,00028 0,00028
2	0,370	0,0003 0,0003 0,0003
3	0,670	0,00033 0,00033 0,00033

2. Вычисление значений – практически,

Анализ графика (график см. на миллиметровке):

Т. к. внешние радиусы колец разные, то и для каждой массы будут разные, а значит, будем иметь три графика. Для каждого графика мы имеем по одной точке , а находим по формуле

• определить значение момента инерции :

- пересечение линии графика оси ординат,

на графике, линии графика пересекают ось ординат в значении:

• определить значение моментов инерции :

- изменение расстояний,

Вычисление значений теоретически:

• нахождение :

• определить значение момента инерции :

• определить значение моментов инерции :

4.Определение натяжения нитей N и N_max:

Если сравнивать силу натяжения нитей с силой тяжести, то мы увидим, что сила натяжения нити примерно равна силе тяжести маятника, а сила натяжения нити max в 2-2,5 раза больше силы тяжести маятника.

3. Определение погрешностей:

1. масса вала+малое кольцо+диск:

2. масса вала+среднее кольцо+диск:

3. масса вала+большое кольцо+диск:

4. радиус вала:

5. погрешность радиусов диск+кольцо:

1. малое кольцо+диск:

2. среднее кольцо+диск:

3. большое кольцо+диск:

6. погрешность радиуса диска:

7. погрешность момента инерции:

Вывод: в ходе работы, мы познакомились с маятником Максвелла, научились определять момент инерции маятника Максвелла. Возникшие расхождения между практическими и теоретическими вычислениями объясняются действием сил сопротивления.