
ФИЗИКА 1 семестр / Отчёты 1 семестр / Закон динамики вращательного движения (Маятник Абербека)
.docНижегородский Государственный Технический Университет
Выксунский филиал
Лабораторная работа 1-8
Изучение основного закона динамики
вращательного движения твердого тела
Выполнила: Герасимова Е. Н.
Группа ПТК - 09
Проверил: Маслов В. П.
2009 год
Цель работы: ознакомление с кинематическими динамическими характеристиками вращательного движения, изучение основного закона динамики вращательного движения твердого тела, экспериментальная его проверка и установление связи момента инерции
твердого тела с распределением его массы относительно оси вращения.
1. Теоретическая часть работы.
Абсолютно твердое тело - тело, расстояния между частицами которого, во время движения не изменяются.
Мерой действия на вращающееся тело является не сила, а момент силы.
![]() (1)
(1)
Мерой инертности при вращательном движении твердого тела является момент инерции.
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
Экспериментальная проверка выполнения основного закона динамики для вращения твердого тела (5):
При
![]() (6)
(6)
При
![]() (7)
(7)
При
![]() в течении времени t
в течении времени t
![]() (8).
(8).
Схема экспериментальной установки (маятник Абербека).

На блок А намотана нить, к которой привязан груз массой m.
2. Вывод основных рабочих формул.
1). Поступательное движение груза m, нити mн и вращательное движение блока А описывается с помощью II и III законов Ньютона:

2). Пусть нить нерастяжима и не скользит по блоку:
![]()
3). Пусть нить невесома, моменты
![]() ,
и
,
и
![]() ,
то в проекциях на оси oY и
oZ :
,
то в проекциях на оси oY и
oZ :
 и, тогда:
и, тогда:
![]() .
.
В то же время момент инерции:
![]()
4). Движение груза m можно
считать равноускоренным, т.к. N=const,
то его ускорение равно:
![]() ,
,
где h - высота, с которой отпускается груз, а t - время его движения (V0=0).
5). Угловую скорость крестовины в конечный
момент падения груза можно вычислить
по формуле:
![]() ,
а изменение её импульса за это же время:
,
а изменение её импульса за это же время:
![]() .
.
Следовательно, равенство (8) принимает
вид:
![]()
3. Исходные данные:
Масса малого груза m1=(0,12851±0,00003)кг
Масса большого груза m2=(0,252±0,003)кг
Масса груза на крестовине m0=(0,14646±0,00003)кг
Высота падения груза h=(0,745±0,001)м
Радиус блока r=(0,018±0,001)м
3.1 Результаты измерений
Таблица 1
|
m,кг |
h,м |
r,м |
R,м |
№ опыта t,с |
<t>,с |
||||
|
1 |
2 |
3 |
4 |
5 |
|||||
|
m1=0,12851 |
0,75 |
0,018 |
R1= 0,033 |
5,8 |
5,8 |
5,7 |
5,6 |
5,6 |
5,7 |
|
R2= 0,22 |
11,6 |
11,6 |
11,4 |
11,8 |
11,3 |
11,5 |
|||
|
R3= 0,12 |
7,9 |
7,8 |
7,9 |
7,9 |
7,8 |
7,8 |
|||
|
R4= 0,065 |
6,3 |
5,9 |
6,1 |
5,9 |
6,3 |
6,1 |
|||
|
R5= 0,18 |
10,4 |
10,3 |
10,8 |
10,1 |
10,6 |
10,4 |
|||
|
m2=0,252 |
0,75 |
0,018 |
R1= 0,033 |
4,1 |
3,8 |
4,1 |
3,8 |
3,8 |
3,9 |
|
R2= 0,22 |
8 |
7,9 |
8,1 |
7,8 |
7,9 |
7,9 |
|||
|
R3= 0,12 |
5,3 |
5,5 |
5,3 |
5,4 |
5,2 |
5,3 |
|||
|
R4= 0,065 |
4,4 |
4,2 |
4,1 |
3,9 |
4,3 |
4,2 |
|||
|
R5= 0,18 |
6,9 |
6,9 |
6,5 |
6,7 |
6,8 |
6,8 |
|||
где
![]() ,
l- расстояние между
грузами m0 , d-длина
груза m0,
,
l- расстояние между
грузами m0 , d-длина
груза m0,
R1 - у оси (крайнее положение)
R2 – на концах (крайнее положение)
R3 – по середине
R4 – четверть (у оси)
R5 – четверть (у концов)
4. Расчеты.
4.1 Определяем ускорение:
![]()
м/с2
Малый груз
![]()
![]()
![]()
![]()
![]()
Большой груз
![]()
![]()
![]()
![]()
![]()
4.2 Определяем угловое ускорение:
![]()
Малый груз
![]()
![]()
![]()
![]()
![]()
Большой груз
![]()
![]()
![]()
![]()
![]()
4.3 Определяем момент силы:
![]()
Малый груз
![]()
![]()
![]()
![]()
![]()
Большой груз
![]()
![]()
![]()
![]()
![]()
4.4 Определяем инертность:
![]()
Малый груз
![]()
![]()
![]()
![]()
![]()
Большой груз
![]()
![]()
![]()
![]()
![]()
4.5 Определяем угловую скорость:
![]()
Малый груз
![]()
![]()
![]()
![]()
![]()
Большой груз
![]()
![]()
![]()
![]()
![]()
4.6 Определяем момент импульса:
![]()
Малый груз
![]()
![]()
![]()
![]()
![]()
Большой груз
![]()
![]()
![]()
![]()
![]()
4.7 Полученные результаты:
Таблица 2
|
№ |
m, кг |
R, м |
a, м/с2 |
, c-2 |
M, Нм |
J, кгм2 |
, c-2 |
L, кг/м2 |
|
Малый груз |
||||||||
|
1 |
m1=0,12852 |
R1= 0,033 |
0,046 |
2,5 |
0,023 |
0,009 |
14,25 |
1,3 |
|
2 |
R2= 0,22 |
0,01 |
0,55 |
0,023 |
0,042 |
6,3 |
0,26 |
|
|
3 |
R3= 0,12 |
0,025 |
1,35 |
0,023 |
0,02 |
11,07 |
0,22 |
|
|
4 |
R4= 0,065 |
0,04 |
2,2 |
0,023 |
0,01 |
13,4 |
0,13 |
|
|
5 |
R5= 0,18 |
0,014 |
0,8 |
0,023 |
0,03 |
8,32 |
0,25 |
|
|
Большой груз |
||||||||
|
1 |
m2=0,252 |
R1= 0,033 |
0,09 |
5 |
0,044 |
0,009 |
19,5 |
0,17 |
|
2 |
R2= 0,22 |
0,02 |
1,1 |
0,044 |
0,04 |
8,7 |
0,35 |
|
|
3 |
R3= 0,12 |
0,05 |
2,8 |
0,044 |
0,02 |
14,8 |
0,3 |
|
|
4 |
R4= 0,065 |
0,08 |
4,4 |
0,044 |
0,01 |
18,5 |
0,2 |
|
|
5 |
R5= 0,18 |
0,03 |
1,7 |
0,044 |
0,025 |
11,6 |
0,35 |
|
5. Проверка на справедливость формул
-
 1)
1) 2)
2)

3)
![]() 4)
4)
![]()
5)
![]()
-
 1)
1) 2)
2)

3)
![]() 4)
4)
![]()
5)
![]()
-
 1)
1)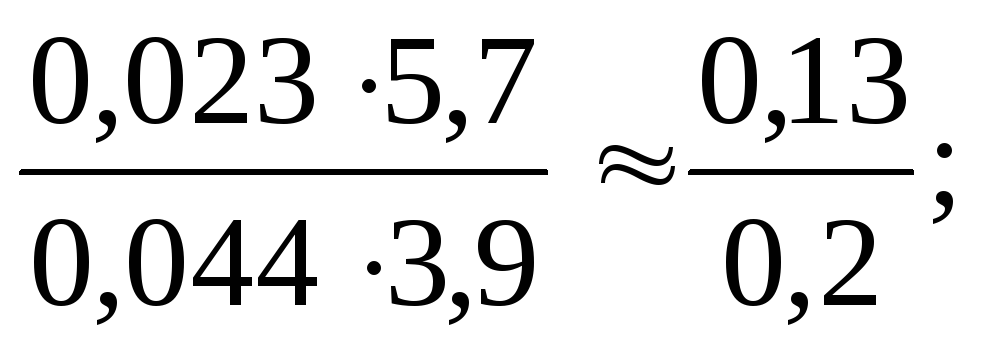 2)
2)

3)![]() 4)
4)![]()
5)![]()
Данные равенства немного нарушаются из-за неточных измерений, погрешностей приборов, внешних воздействий на систему и т.п.
6. Расчет инерции теоретически (вращающейся части установки)
![]()
Малый груз
![]()
![]()
![]()
![]()
![]()
Большой груз
![]()
![]()
![]()
![]()
![]()
Таблица 3.
-
№
m, кг
R, м
R2, м2
h, м
<t>, c
J, кгм2
Малый груз
1
0,12851
0,033
0,001
0,75
5,7
0,009
2
0,12851
0,22
0,05
0,75
11,5
0,04
3
0,12851
0,12
0,0144
0,75
7,8
0,02
4
0,12851
0,065
0,004
0,75
6,1
0,01
5
0,12851
0,18
0,0324
0,75
10,4
0,03
Большой груз
1
0,252
0,033
0,001
0,75
3,9
0,008
2
0,252
0,22
0,05
0,75
7,9
0,03
3
0,252
0,12
0,0144
0,75
5,3
0,02
4
0,252
0,065
0,004
0,75
4,2
0,009
5
0,252
0,18
0,0324
0,75
6,8
0,025
7.Анализ графических результатов (графики см. на миллиметровке):
![]()

Малый груз
a).
![]()
б).
![]()
в).
![]()
г)
![]()
Большой груз
a).
![]()
б).
![]()
в).
![]()
г)
![]() т.
к. в экспериментальной установке
существует сила трения, которую мы не
учитывали при расчетах; также существует
погрешности приборов и т.п.
т.
к. в экспериментальной установке
существует сила трения, которую мы не
учитывали при расчетах; также существует
погрешности приборов и т.п.
8. Расчет погрешностей.
5.1 Погрешность момента инерции:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Малый
груз
Малый
груз
1)![]()
![]()
![]()
![]()
![]()
2)![]()
![]()
![]()
![]()
![]()
Большой груз
1)![]()
![]()
![]()
![]()
![]()
2)![]()
![]()
![]()
![]()
![]()
Вывод:
В ходе работы мы ознакомились с характеристиками вращательного движения, экспериментально проверили основной закон динамики вращательного движения, а также установили связь момента инерции твердого тела с распределением его массы относительно оси вращения.
