ФИЗИКА 1 семестр / Отчёты 1 семестр / Власов В. - Механич. удар

Нижегородский государственный технический университет

Выксунский филиал

Лабораторная работа по физике № 2

Механический удар

Выполнил:

Студент группы ЭПА-07 Власов В.И.

Принял:

Маслов В.П.

Выкса

2007 г.

Цель работы: Ознакомиться с элементами теории механического удара и экспериментально определить время удара ,среднюю силу удара и коэффициент восстановления .

Практическая ценность работы: Изучение основных характеристик удара и знакомство с цифровыми приборами для измерения временных интервалов.

Краткая теория вопроса

Ударом называется изменение состояния движения тела вследствие кратковременного взаимодействия его с другим телом. Линия удара это нормаль к плоскости касания соударяющихся тел, проведенная через точку удара. Если она проходит через центры тяжести соударяющихся тел, то удар называют центральным, в противном случае – нецентральным. Если скорости соударяющихся тел направлены вдоль линии удара, то его называют прямым, в противном случае непрямым или косым. Промежуток времени, в течение которого длится удар, обычно достаточно мал, а развивающиеся на площадках контакта соударяющихся тел силы (ударные силы) очень велики. Во время удара оба тела претерпевают изменения формы (деформацию).

Сущность упругого удара заключается в том, что кинетическая энергия относительного движения соударяющихся тел за короткое время преобразуется в энергию упругой деформации и в той или иной степени в энергию упругой деформации и в той или иной степени в энергию молекулярного движения. В процессе удара происходит перераспределение энергии между соударяющимися телами.

Процесс удара, начинающийся с момента соприкосновения соударяющихся поверхностей, можно разделить на две фазы. В течение первой фазы происходит сближение соударяющихся тел. При этом кинетическая энергия системы уменьшается, а относительная скорость убывает до нуля. Вслед за этим наступает вторая фаза удара: тела начинают удаляться друг от друга, частично или полностью восстанавливая свою форму, а кинетическая энергия и относительная скорость их возрастает. Когда площадь поверхности соприкосновения тел обращается в нуль, тела прекращают контакт, процесс удара заканчивается.

При абсолютно упругом ударе уравнение энергетического баланса имеет вид:

.

При абсолютно неупругом ударе:

,

где ΔU – изменение внутренней энергии тел системы.

Наблюдения показывают, что относительная скорость тел после удара не достигает своего прежнего численного значения. Это объясняется тем, что на практике мы никогда не имеем дело с идеально упругими деформациями тел.

Пусть на плоскую поверхность массивной пластины падает шар с некоторой скоростью и отскакивает от нее со скоростью (см. рис. 1).

Обозначим Vn1, Vτ1, Vn2, Vτ2 – нормальные и тангенциальные составляющие скоростей и , а β1 и β2 – составляющие скоростей падения и отражения и их касательные составляющие были бы равны Vn1=Vn2; Vτ1=Vτ2. Это означало бы, что скорость шара до удара равна его скорости после удара V1=V2, а также угол падения равен углу отражения β1=β2. В условиях реального удара всегда происходит частичная потеря механической энергии, вследствие чего как нормальные, так и тангенциальные составляющие скорости после удара уменьшаются Vn2<Vn1; Vτ2<Vτ1.

Отношение числового значения нормальной составляющей относительной скорости после удара к ее величине до удара есть физическая характеристика, зависящая от природы сталкивающихся тел,

.

Эту характеристику ε называют коэффициентом восстановления. Числовое значение его лежит между 0 и 1.

ε=0 указывает на то, что взаимодействующие тела абсолютно неупруги, восстановление формы их после удара не происходит, и оба тела движутся в дальнейшем как одно целое. При этом оказывается, что часть механической энергии израсходована на работу деформации и превращена во внутреннюю энергию тел.

Если ε=1, то взаимодействующие тела называются абсолютно упругими. В этом случае изменение формы тел, происходящее в начале удара, полностью устраняется при его завершении. Механическая энергия системы взаимодействующих тел сохраняется. В действительности для всех тел коэффициент восстановления имеет значение 0<ε<1.

Схема экспериментальной установки

Экспериментальная установка состоит из стального шарика А, подвешенного на нитях, и неподвижного тела В

большой массы, с которым шарик соударяется. Угол отклонения подвеса измеряется по шкале. В момент удара на шар массой действует сила тяжести со стороны Земли, сила реакции опоры нити , средняя сила удара со стороны тела В.

Длительность ударашарика о плиту определяется по показаниям частотомера ЧЗ-54.

По теореме об изменении импульса материальной точки

(2)

где и - векторы скоростей до и после удара, - длительность удара.

После проецирования на ось x определим среднюю силу удара:

(3)

Скорости шарика определяются на основании теоремы об изменении механической энергии системы “шар-Земля”, энергия которой не меняется:

(4)

Из чертежа следует, что

Находим значения начальной и конечной скоростей шарика: (5)

Коэффициент восстановления для каждого случая .

Результаты опыта:

№ опыта	20 0		30 0		40 0		50 0		60 0
	, мкс.	, 0	, мкс.	, 0	, мкс.	, 0	, мкс.	, 0	, мкс.	, 0
1	30,5	16,5	28,2	25,6	26,5	32	25,8	40	25,0	48
2	30,5	16,5	27,9	25,6	26,7	33	25,6	41	25,3	47
3	30,7	16,5	28,0	25,6	26,3	33	25,9	39	25,2	47
4	30,2	17	28,1	25,6	26,6	32,5	25,8	41	25,1	48
5	30,0	16,8	28,4	25,2	26,5	32,5	25,8	40	25,1	47,5
6	30,5	17	28,2	25,2	26,5	33	25,6	40	25,3	48
7	30,3	16,5	28,1	25,6	26,8	33	25,7	41	25,0	47,5
8	30,4	17	28,3	25,2	26,3	33,5	25,7	40	25,0	47
9	30,6	16,5	28,0	25,2	26,5	33	25,8	40	25,2	48
10	30,5	17	28,2	25,6	26,4	32,5	25,8	40	25,3	48
Среднее значение	30,42	16,73	28,14	25,44	26,51	32,8	25,75	40,2	25,15	47,6

Измерение длины нити:

l ₁ = 0,325 м

l ₂ = 0,323 м

l ₃ = 0,324 м

l ₄ = 0,326 м

l ₅ = 0,326 м

l ₆ = 0,323 м

l ₇ = 0,327 м

l ₈ = 0,324 м

l ₉ = 0,324 м

l ₁₀ = 0,325 м

<l> =0,325м

Измерение массы шарика:

m1=m2=m3=m4=m5=18,83кг

Расчёты:

=20⁰

=30⁰

=40⁰

=50⁰

=60⁰

Расчёт погрешности исходных данных

Расчёт погрешности для начального угла

Расчет погрешности прямых измерений

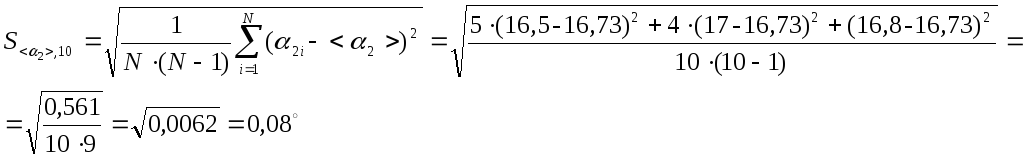
=(мкс)

=0,16 (мкс)

=(30,42+0,16)мкс, %, Р=95%.

Расчёт погрешностей косвенных измерений:

1. Погрешность скорости:

2. Погрешность средней силы удара:

, где

,

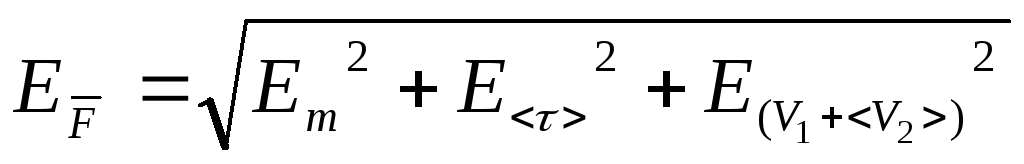Из таблицы результатов находим значения и уже найденное и

рассчитываем искомую погрешность :

_{Результаты расчетов}

	< >,Н	,м/с	< >,мкс		,Н	,м/с	,мкс	,м/с
200	669	0,61	30,42	0,85	20	0,03	0,16	0,52
300	1087	0,92	28,14	0,84				0,78
400	1511	1,22	26,51	0,82				1,005
500	1903	1,50	25,75	0,81				1,22
600	2400	1,78	25,15	0,80				1,43

Вывод:

В ходе работы мы ознакомились с элементами теории механического удара, экспериментально определили временные интервалы удара, среднюю силу и коэффициент восстановления. Для уменьшения погрешности измерений было проведено по 10 опытов для 5 различных углов отклонения.

При расчёте погрешностей (для угла отклонения ) было найдено, что относительные погрешности искомых величин не превышают , следовательно, теория механического удара хорошо согласуется с экспериментальным определением времени удара , средней силы удара F, коэффициента восстановления .

Очевидно, что минимальные погрешности были обусловлены достаточно малой погрешностью частотомера (мкс.) и оптимальным количеством проведённых опытов.

8