Нижегородский Государственный

Технический Университет

Выксунский Филиал

Лабораторная работа

по общей физике

“ Определение отношения теплоемкостей воздуха при постоянном давлении и постоянном объеме методом Клемана-Дезорма. ”

Выполнили:

Немировская Е. А.

Астраханцева Е.М.

Группа: ЭПА-07

Проверил:

Маслов В.П.

г. Выкса

2007г.

1. Цель работы: ознакомление с методом Клемана-Дезорма и определение отношения молярных теплоемкостей воздуха при постоянном давлении и постоянном объеме.

2. Теоретические основы. Теплоемкостью тела называется величина, равная количеству теплоты, необходимому для нагревания этого тела на один Кельвин. Она зависит от массы тела, его химического состава и вида процесса сообщения теплоты. Теплоемкость одного моля вещества называется молярной теплоемкостью с_М. Согласно первому началу термодинамики тепло dQ, сообщенное системе, расходуется на увеличение внутренней энергии системы dU и совершение системой работы dA против внешних сил dQ=dU+dA. (1)

При нагревании газа при постоянном объеме (dV=0) работа газа dA=рdV равна нулю, поэтому молярная теплоемкость

, (2)

где i – число степеней свободы – количество независимых координат, с помощью которых однозначно можно задать положение молекулы.

При изобарном нагревании (p=const) тепло, подведенное к газу, расходуется на увеличение внутренней энергии и на совершение работы расширения газа . Теплоемкость моля газа при этом равна

. (3)

Сравнивая (2) и (3), получим . (4)

Уравнение (4) представляет собой уравнение Майера для молярных теплоемкостей.

Для идеальных газов отношение зависит только от числа степеней свободы молекул газа, которое в свою очередь определяется структурой молекулы, т.е. количеством атомов, из которых состоит молекула. Одноатомная молекула имеет три степени свободы (инертные газы). Если молекула состоит из двух атомов, то число степеней свободы складывается из числа степеней свободы поступательного движения центра масс и вращательного движения системы вокруг двух осей, перпендикулярных к оси молекулы, т.е. равно пяти. Для трех и многоатомных молекул имеются три поступательные и три вращательные степени свободы, т.е. i = 6.

3. Экспериментальная часть

3.1. Краткое описание экспериментальной установки и оборудования.

Схема экспериментальной установки представлена на рис.1: 1 – блок манометра; 2 – приборный блок; 3 – колба; 4 – пневмотумблер «АТМОСФЕРА»; 5 – тумблер включения насоса для подачи воздуха в колбу; 6 – тумблер включения питания установки.

Если при помощи насоса накачать в сосуд некоторое количество воздуха, то давление и температура воздуха внутри сосуда повысятся. Вследствие теплообмена воздуха с окружающей средой через некоторое время температура воздуха, находящегося в сосуде, сравняется с температурой внешней среды .

Давление, установившееся в сосуде, равно P₁= P₀+P’, где P₀ – атмосферное давление, P’=h₁k – добавочное давление, пропорциональное разности уровней жидкости в манометре h₁ (рис. 2), k – коэффициент пропорциональности. Таким образом, воздух внутри сосуда характеризуется параметрами P₀+P’, V₀, Т₀. Уравнение состояния примет вид:

, (6)

где m – масса воздуха в сосуде, М – молярная масса воздуха.

Если на короткое время (~3с) открыть тумблер «АТМОСФЕРА», то воздух в сосуде будет расширяться. Этот процесс расширения можно рассматривать как подключение к сосуду дополнительного объема V’. Давление в сосуде установится равным атмосферному Р₀, температура понизится до Т₁, а объем будет равен V₀+V’. Следовательно, в конце процесса уравнение состояния примет вид

. (7)

Разделив выражение (7) на выражение (6), получим . (8)

Расширение происходит без теплообмена с внешней средой, т.е. процесс является адиабатическим, поэтому для начального и конечного состояния системы применимо соотношение

или . (9)

Охладившийся при расширении воздух через некоторое время, вследствие теплообмена с внешней средой, нагреется до комнатной температуры Т₀ (изохорический процесс). Давление возрастет до некоторой величины P₂= P₀+P’’, где P’’=h₂k – новое добавочное давление, пропорциональное разности уровней жидкости в манометре h₂. Для воздуха массой m’ оставшегося в сосуде уравнение состояния начала нагрева . (10)

В конце нагрева до комнатной температуры Т₀ . (11)

Разделив (10) на (11), получим . (12)

Правые части выражений (8) и (12) одинаковы, следовательно, левые части также равны

или . (13)

Возведя левую и правую часть (13) в степень , запишем . (14)

Заменим правую часть (14) с учетом (9) 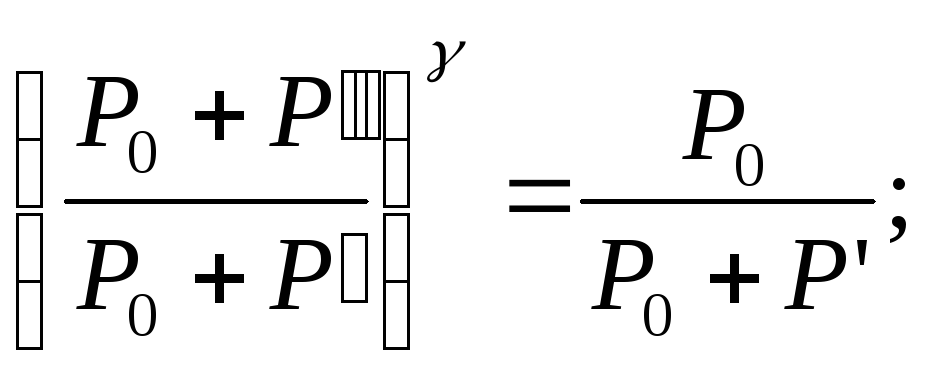откуда (15)

т.к. то, ограничиваясь первым членом разложения в ряд бинома и пренебрегая членами второго порядка малости, получим

. (16)

3.2. Методика проведения эксперимента.

1. Подать на установку питание, включив тумблер 6 «СЕТЬ».

3.2.2.Включить подачу воздуха в колбу тумблером «ВКЛ» в модуле «ВОЗДУХ». При этом пневмотумблер «АТМОСФЕРА» должен находиться в нижнем положении.

2. По манометру 1 контролировать рост давления в колбе. После достижения заданного уровня рабочего давления (150250) отключить подачу воздуха тумблером «ВКЛ».

3.2.4. После стабилизации давления (в течение 2-3 минут) снять показание h₁ манометра 1. Результат занести в таблицу.

3.2.5. Переключить пневмотумблер «АТМОСФЕРА» в верхнее положение и держать его так до тех пор, пока давление в колбе не упадет до нуля, после чего резко опустить пневмотумблер вниз.

3.2.6. После стабилизации процесса (2-3 минуты), снять показания h₂ манометра 1 определяющее давление, возросшее за счет теплообмена до комнатной температуры(?). Результат занести в таблицу.

3.2.7. Опыт провести 5 раз, изменяя величину h₁.

3.3. Обработка результатов измерений.

3.3.1. Подставить в формулу (16) полученные значения h₁ и h₂, взятые из каждого отдельного опыта, вычислить ₁, ₂ и т.д. Результаты занести в таблицу.

3.3.2. Определить среднее значение _ср, среднюю абсолютную ошибку _ср.

№ опыта	h1, мм	h2, мм
1
2
3
4
5
Средние значения

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Сформулировать первое начало термодинамики. Объяснить смысл и выражения для теплоты, внутренней энергии и работы.

2. Что называется теплоемкостью?

3. Какой физический смысл имеют С_р и С_v? Как они связаны?

4. Что такое ? Как она связана с теплоемкостями C_p и C_v?

5. Записать уравнение Менделеева-Клапейрона.

6. Физический смысл универсальной газовой постоянной.

7. Записать уравнения изохорического и адиабатического процессов.

8. Какой процесс называется адиабатическим? Уравнение адиабаты. Что происходит с внутренней энергией и температурой при адиабатическом расширении или сжатии?

9. Вывести расчетную формулу (10).

10. Какие процессы различают в этой работе?

Уравнение Пуассона:

,

,

.

– показатель адиабаты.

Ход работы.

1. По формуле находим показатель адиабат и записываем в таблицу:

N»№
11	0.18	0.02	1.125
22	0.185	0.015	1.088
33	0.175	0.01	1.06
44	0.20	0.02	1.11
55	0.15	0.007	1.049

1.0864

2. Находим абсолютные погрешности:

0.0386 0.0016

-0.0264 0.0236 -0.0374

3. Находим среднеквадратичную абсолютную погрешность серии измерений:

0.03996

4. Находим относительную погрешность измерений:

3.68%.

Вывод: Изучили адиабатический процесс в газах; определили отношение теплоемкостей газа методом адиабатического расширения.