ФИЗИКА 1 семестр / Отчёты 1 семестр / лаба7

Цель работы: определение отношения теплоемкостей γ=C_P/C_V на основе изучения процесса распространения звуковой волны и измерения резонансным методом скорости звука при различных температурах воздуха.

Методика измерений.

Упругими волнами называются механические возмущения (деформации), распространяющиеся в упругой среде. Звуковыми, или акустическими волнами называются упругие волны малой интенсивности. Звуковые волны, способные вызвать звуковые ощущения, воздействующие на органы слуха человека, имеют частоты в пределах от 16 до 20000 Гц.

Рассмотрим распространение звуковой волны в газе. Как известно, выражение для скорости продольных упругих волн в сплошной среде имеет вид:

, (1)

где k – модуль объемной упругости*; ρ – плотность невозмущенной среды.

Звуковая волна представляет собой перемещающуюся в пространстве последовательность чередующихся областей сжатия и разрежения газа. Сжатия и разрежения сменяют друг друга настолько быстро, что теплообмен между слоями газа, имеющими разные температуры, не успевает произойти. Поэтому процесс распространения звуковой волны в газе можно считать адиабатическим.

Выразим модуль объемной упругости k через добавочное давление Δр, вызывающее сжатие газа, и относительную объемную деформацию ΔV/V:

.

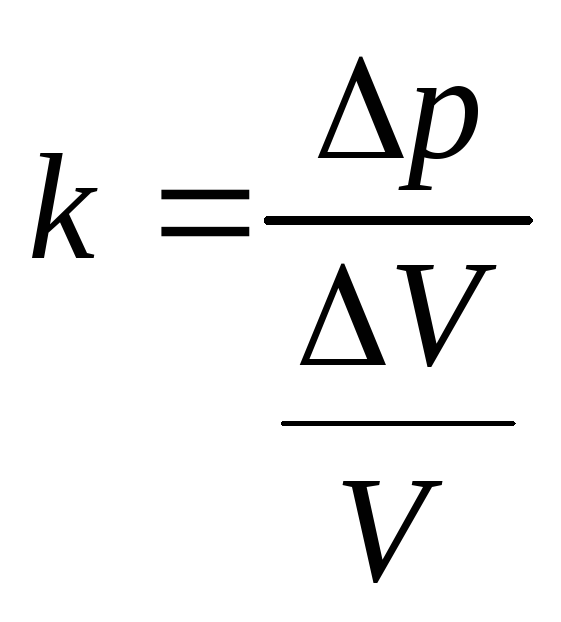Полагая изменения давления dp и объема dV бесконечно малыми, можно записать:

, (2)

где знак минус означает, что увеличению давления соответствует уменьшение объема.

Дифференцируя уравнение Пуассона , описывающее адиабатический процесс в газе, получим:

,

откуда

. (3)

Решив совместно (2) и (3), найдем

. (4)

Определяя плотность газа из уравнения состояния , где R – универсальная газовая постоянная, R=8,31 Дж/(моль·К), получаем:

, (5)

и подставляя (4) и (5) в (1), получаем формулу Лапласа для расчета скорости звука в газе:

, (6)

из которой следует

. (7)

Таким образом, для определения отношения теплоемкостей газа γ достаточно измерить его температуру и скорость распространения звука в нем.

Скорость звука при заданной температуре газа может быть найдена резонансным методом. При распространении волны вдоль закрытого канала она многократно отражается от торцов. Звуковые колебания в канале являются наложением всех отраженных волн и достаточно сложны. Картина упрощается, если длина канала равна целому числу полуволн:

, (8)

где n – любое целое число: λ – длина волны.

Если условие (8) выполнено, то волна, отраженная от торца канала, вернувшаяся к его началу и вновь отраженная, совпадает по фазе с падающей волной. совпадающие по фазе волны усиливают друг друга. Амплитуда звуковых колебаний при этом резко возрастает – наступает резонанс.

При звуковых колебаниях слои газа, прилегающие к торцам канала, не испытывают смещения. В этих местах образуются узлы смещения. Они повторяются по всей длине канала через λ/2. Между узлами находятся максимумы смещения (пучности).

Скорость звука V связана с частотой колебаний υ и длиной волны λ соотношением:

. (9)

Подставляя (8) в (9), получаем линейную зависимость резонансной частоты от номера резонанса:

, (10)

где υ_р – резонансная частота.

Зависимость (10) может быть проверена экспериментально. Изменяя частоту колебаний при постоянной длине канала, строят график υ_p=f(n) и по тангенсу угла наклона прямой к оси абсцисс α определяют скорость звука

. (11)

Расчёт:

tg₁ = 202,14; tg₂ = 205,71; tg₃ = 209,29

Т₁=273+20=291 Кº М=29*10^-3 кг/моль

Т₂=273+40=313 Кº L=0,61 м

Т₃=273+60=333 Кº R=8,31 Дж/К*моль

Определяем скорость звука:

V₁=2*0,61*202,14=246,6 м/с

V₂=2*0,61*205,71=251 м/с

V₃=2*0,61*209,29=255,3 м/с

Определяем отношение теплоёмкостей:

₁=

₂=

₂=

Таблица1:

№ рез-са	t1 комн., 0С (20 0С)			t2 , 0С (40 0С)			t3 , 0С (60 0С)
	р, Гц	V, м/с		р,Гц	V,м/с		р,Гц	V,м/с	
1	370	246,6	0,73	400	251	0,7	420	255,3	0,68
2	520			560			590
3	660			720			780
4	840			870			890
5	1030			1040			1090
6	1170			1180			1250
7	1700			1800			1830

Вывод: В этой работе мы научились определять отношение теплоёмкостей на основе изучения процесса распространения звуковой волны и измерения резонансным методом скорости звука при различных температурах.

График:

3