Для магнитного поля, как и для электрического, справедлив принцип суперпозиции:

i

3.5. Закон полного тока для магнитного поля в вакууме. Теорема Гаусса для поля Β

Циркуляция вектора Βr по произвольному замкнутому контуру равна произведению магнитной постоянной μ0 на алгебраическую сумму токов, ох-

ватываемых этим контуром:

Ток Ik считается положительным, если его направление связано с направлением обхода по контуру правилом правого винта.

Потоком вектора магнитной индукции через площадку dS называется скалярная физическая величина, равная

Это означает, что линии вектора Β являются замкнутыми.

ГЛАВА 4 Электромагнитная индукция

4.1. Основной закон электромагнитной индукции

При всяком изменении магнитного потока, пронизывающего контур, в нем возникает ЭДС электромагнитной индукции.

S

Используя закон Ома для полной цепи и основной закон электромагнитной индукции (4.1), можно получить выражение для индукционного тока:

4.2. Самоиндукция. Индуктивность

Возникновение ЭДС индукции в проводящем контуре при изменении в нем силы тока называют самоиндукцией.

При отсутствии вблизи контура с током ферромагнетиков полный маг-

где L - коэффициент, называемый индуктивностью контура. Индуктивность L зависит от размеров и формы контура, а также от магнитных свойств окружающей среды. Единицей индуктивности является генри (Гн).

При изменении магнитного потока в контуре возникает ЭДС самоиндукции εS :

εS = − ddФt = − ddt (LI ).

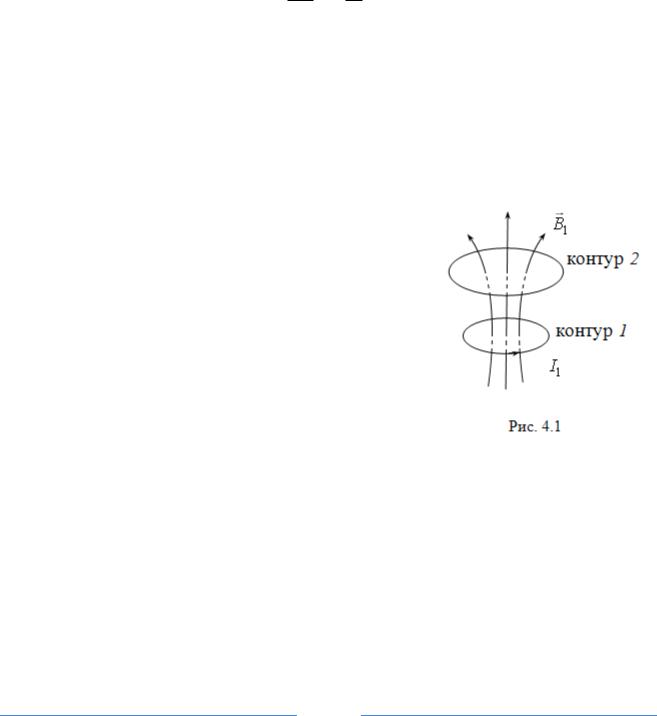
4.3. Взаимная индукция

Возникновение ЭДС в одном контуре при изменении силы тока, протекающего по другому контуру, называют взаимной индукцией.

Рассмотрим два неподвижных друг относительно друга контура (рис.4.1), по одному из которых течет ток I1 , создающий магнитное поле Β1 .

Согласно (3.9), Β1 ~ I1 , поэтому магнитный поток, созданный током I1 и пронизывающий контур 2, Ф21 ~ I1 . Тогда можно записать:

где L21 - взаимная индуктивность - коэффициент пропорциональности, завися-

щий от размеров обоих контуров, их взаимного расположения и магнитной проницаемости окружающей среды.

Задав ток I2 в контуре 2 и проведя аналогичные рассуждения для потока Ф12 , созданного током I2 и пронизывающего контур 1, запишем:

21

Коэффициенты пропорциональности L12 и L21 равны между собой ( L12 = L21 ) и называются взаимной индуктивностью контуров. Единицей измерения для них так же, как и для индуктивности, является генри (Гн).

ГЛАВА 5 Электрические колебания

5.1.Собственные незатухающие колебания

Вцепи (рис. 5.1), содержащей катушку индуктивности L , конденсатор емкости С и сопротивление R , могут возникнуть электрические колебания. Такая

цепь называется колебательным контуром.

Пусть вначале нижняя обкладка конденсатора заряжена положительно, а верхняя – отрицательно.

При этом вся энергия сосредоточена в конденсаторе. Замкнем ключ К. Конденсатор начнет разряжаться, через катушку и сопротивление потечет ток I . Электрическая энергия конденсатора начнет превращаться в магнитную энергию катушки и джоулево тепло в сопротивлении.

Для мгновенных значений тока, которые оказываются практически одинаковыми на всех участках цепи (такой ток называют квазистационарным), запишем закон Ома:

Это есть уравнение колебательного контура – линейное однородное дифференциальное уравнение второго порядка. Уравнение колебательного контура можно записать в ином виде:

Величина ω0 называется собственной частотой свободных колебаний контура, δ - коэффициентом затухания. При отсутствии в контуре потерь на

22

джоулево тепло и на излучение (R=0) колебания будут незатухающими, при наличии потерь (R ≠ 0 ) – затухающими.

В отсутствие потерь уравнение (5.4) принимает вид

где q0 - амплитудное значение заряда на обкладках конденсатора; ω0 - собст-

5.2.Собственные затухающие колебания. Вынужденные колебания

Вреальном контуре свободные колебания всегда являются затухающими и описываются уравнением (5.4). При достаточно малых потерях (δ< ω0 )

решение этого уравнения имеет вид

Функция (5.9) определяет затухающие колебания. Множитель q0e−δt в (5.9) называется амплитудой затухающих колебаний.

Величина T = 2πω называется периодом затухающих колебаний:

где T0 - период свободных незатухающих колебаний. График функции (5.9) показан на рис. 5.2.

23