Многочлены Чебышева.

Погрешности могут быть распреде­лены неравномерно но рассматриваемому интервалу изменения аргумента. Одним из способов совершенство­вания алгоритма вычислений, позволяющих более равномерно распределить погрешность по всему интервалу, является использование многочленов Чебышева.

Многочлен Чебышева степениопределяется следующей формулой:

, (6)

,.

Приведем многочлены Чебышева, полученные по формуле (6) при .

Для вычисления многочленов Чебышева можно воспользоваться рекуррентным соотношением,(7).

В ряде случаев важно знать коэффициент при старшем члене многочлена Чебышева степени

.

Перейдем к пределу при и воспользуемся формулой (6). Получим

Многочлены Чебышева можно представить в тригонометрической форме:

(8).

Нули (корни) многочленов Чебышева на отрезке определяются формулой

.

Они расположены неравномерно на отрезке и сгущаются к его концам. Вычисляя экстремумы многочлена Чебышева по обычным правилам (с помощью производных), можно найти его максимумы и минимумы:

.

В этих точках многочлен принимает поочередно значения , т.е. все максимумы равны 1, а минимумы равны -1. На границах отрезка значения многочленов Чебышева равны1.

Приведем формулы, необходимые при использовании многочленов Чебышева.

1. Многочлены Чебышева:

,

2. Представление степенейчерез многочлены:

3. Выражениечерез более низкие степени:

Вычисление многочленов в лоб требует выполнитьумножений исложений.

Для исключения возведения в степень в каждом члене, многочлен целесообразно переписать в виде:

.

Этот прием называется схемой Горнера. Метод требует умножений исложений.

Алгоритм метода Горнера.

Использование схемы Горнера экономит машинное время и повышает точность вычислений за счет уменьшения погрешностей округления.

Линейная и квадратичная интерполяция.

Простейшим видом локальной интерполяции является линейная интерполяция. Она состоит в том, что заданные точ­ки соединяются прямолинейными отрезками, и функцияприближается ломаной с вершинами в данных точках.

Уравнения каждого отрезка ломаной в общем случае разные. По­скольку имеется интервалов, то для каждого из них в ка­честве уравнения интерполяционного многочлена используется уравнение прямой, проходящей через две точки. Для-го интервала можно написать уравнение прямой, проходящей через точкии, в виде

.

Отсюда

(9).

При использовании линейной интерполяции сна­чала нужно определить интервал, в который попадает значение аргу­мента , а затем подставить его в формулу (9) и найти приближенное значение функции в этой точке.

Блок-схема линейной интерполяции.

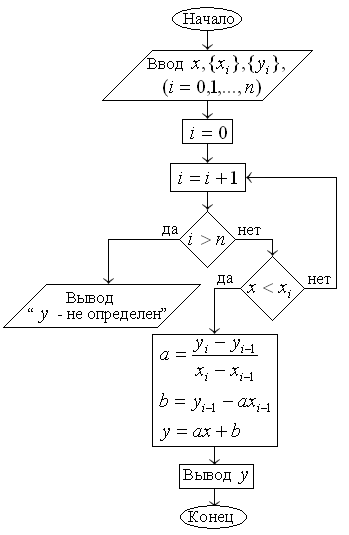
Рассмотрим случай квадратичной интерполяции. В качестве интерполяционной функции на отрезке принимается квад­ратный трехчлен. Такую интерполяцию называют параболической.

Уравнение квадратного трехчлена

(10).

Содержит три неизвестных коэффициента , для определения которых необходимы три уравне­ния. Ими служат условия прохожде­ния параболы (10) через три точки. Эти условия можно записать в виде

(11).

Блок-схема алгоритма такая же, как и для линейной интерполяции . Только нужно использовать формулы (10) с учетом решения системы линейных уравнений (11). Интерполяция для любой точки проводит­ся по трем ближайшим к ней узлам.