Метод золотого сечения.

При построении процесса оптимизации стараются сократить объем вычислений и время поиска. Этого достига­ют обычно путем сокращения количества вычислений (или измерений при проведении эксперимента) значений целевой функции . Одним из наиболее эффективных методов, в которых при ограниченном коли­честве вычисленийдостигается наилучшая точность, является ме­тод золотого сечения. Он состоит в построении последовательности отрез­ков, стягивающихся к точке минимума функции. На каждом шаге, за исключением первого, вычисление значения функциипроводится лишь один раз. Эта точка, называемая золотым сечением, выбирается специальным образом.

Поясним сначала идею метода геометрически, а затем выведем необхо­димые соотношения.

Нaпервом шаге процесса оптимизации внутри отрез­ка(рис. а) выбираем некоторые внутренние точкии, и вычисляем значении целевой функциии. Поскольку в данном случае, очевидно, что минимум расположен на одном из прилегающих котрезков:или. Поэтому отрезокможно отбросить, сузив тем самым первоначальный интервал неопреде­ленности.

Второй шаг проводим на отрезке (рис. 6),. Нужно снова выбрать, две внутренние точки, но одна из них () осталась из предыдущего шага, поэтому достаточно выбрать лишь одну точку, вычислить значениеи провести сравнение. Поскольку здесь, ясно, что минимум находится на отрезке. Обозначим этот отрезок, снова выберем одну внутреннюю точку и повторим процедуру сужения интервала неопределенности. Процесс оптимизации повторяется до тех пор, пока длина очередного отрезкане станет меньше заданной величины.

Теперь рассмотрим способ размещения внутренних точек на каждом отрезке . Пусть длина интервала неопределенности равна, а точка деления разбивает его на части. Золотое сече­ние интервала неопределенности выбирается так, чтобы отношение длины большего отрезка к длине всего интервала равнялось отношению длины меньшего отрезка к длине большего отрезка:

(1).

Из этого соотношения можно найти точку деления, определив отношение . Преобразуем выражение (1) и найдем это значение:

,,,

,

Поскольку нас интересует только положительное решение, то

.

Отсюда ,. Поскольку заранее известно, в какой последовательности (иилии) делить интервал неопределенности, то соответствующие двум этим способом деления.

На рис.точки деленияивыбираются с учетом полученных значений для частей отрезка. В данном случае имеем

.

После первого шага оптимизации получается новый интервал неопределенности – отрезок (рис.). Можно показать, что точкаделит этот отрезок в требуемом отношении, при этом,. Для этого проведем очевидные преобразования:

,

,

.

Вторая точка деления выбирается на таком же расстоянии от левой границе отрезка, т.е..

И снова интервал неопределенности уменьшается до размера

.

Используя полученные соотношения можно записать координаты точек деления иотрезкана-м шаге оптимизации:

.

При этом длина интервала неопределенности равна

.

Процесс оптимизации заканчивается при выполнении условия . При этом проектный параметр оптимизации составляет. Можно в качестве оптимального значения принять(или, илии т.п.).

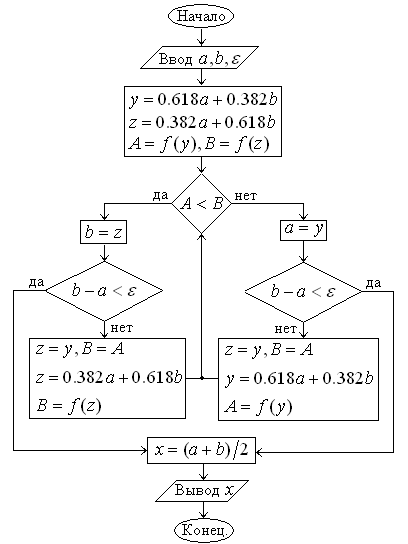
Блок-схема метода золотого сечения:

.

Многомерные задачи оптимизации.

Минимум функции нескольких переменных.В большинстве реальных задач оптимизации, представляющих практический интерес, целевая функция зависит от многих проектных параметров.

Минимум дифференцируемой функции многих пере­менных можно найти, исследуя ее значения в критических точках, которые определяются из решения системы дифференциальных уравнений

(2).

Рассмотренный метод можно использовать лишь для дифференцируемой целевой функции. Но и в этом случае могут возникнуть серьезные трудности при решении си­стемы нелинейных уравнений (2).

Во многих случаях никакой формулы для целевой функции нет, а имеется лишь возможность определения ее значений в произвольных точках рассматриваемой об­ласти с помощью некоторого вычислительного алгоритма или путем физических измерений. Задача состоит в при­ближенном определении наименьшего значения функции во всей области при известных ее значениях в отдельных точках.

Для решения подобной задачи в области проектирова­ния , в которой ищется минимум целевой функции, можно ввести дискретное множество точек (узлов) путем разбиения интервалов изменения параметровна части с шагами. В полученных узлах можно вычислить значения целевой функции и среди этих значений найти наименьшее.

Следует отметить, что такой метод может быть исполь­зован для функции одной переменной. В многомерных за­дачах оптимизации, где число проектных параметров до­стигает пяти и более, этот метод потребовал бы слишком большого объема вычислений.

Оценим, например, объем вычислений с помощью об­щего поиска при решении задачи оптимизации функции пяти неизвестных. Пусть вычисление ее значения в од­ной точке требует арифметических операций (на практике это число может достигать нескольких тысяч и больше). Область проектирования разделим нача­стей в каждом из пяти направлений, т. е. число расчет­ных точек равно, т. е. приблизительно. Число, арифметических операций тогда равно, и для реше­ния этой задачи на ЭВМ с быстродействием 1 млн. оп./с. потребуетсяс (более 10 суток) машинного времени.

Проведенная оценка показывает, что такие методы об­щего поиска с использованием сплошного перебора для решения многомерных задач оптимизации не годятся. Не­обходимы специальные численные методы, основанные на целенаправленном поиске. Рассмотрим некоторые из них.

Метод покоординатного спуска. Пусть требуется найти наименьшее значение целевой функции. В качестве начального приближения выберем в-мерном пространстве некоторую точку, с координатами. Зафиксируем все координаты функции, кроме первой. Тогда- функция одной переменной. Решая одномерную зада­чу оптимизации для этой функции, мы от точкипере­ходим к точке, в которой функцияпринимает наименьшее значение по координате при фиксированных остальных координатах. В этом состо­ит первый шаг процесса оптимизации, состоящий в спус­ке по координате.

Зафиксируем теперь все координаты, кроме , и рас­смотрим функцию этой переменной. Снова решая одномерную задачу оптимизации, находим ее наименьшее значение прит. е. в точ­ке. Аналогично проводит­ся спуск по координатам, а затем процедура снова повторяется отдот. д. В результате этого процесса получается последовательность точек, в которых значения целевой функции составляют моно­тонно убывающую последовательность. На любом-м шаге этот процесс можно прервать, и зна­чениепринимается в качестве наименьшего значе­ния целевой функции в рассматриваемой области.

Таким образом, метод покоординатного спуска сводит задачу о нахождении наименьшего значения функции многих переменных к много­кратному решению одномерных задач оптимизации по каждому проектному пара­метру.

Данный метод легко про­иллюстрировать геометриче­ски для случая функции двух переменных , описывающей некоторую поверхность в трехмерном пространстве. На рисунке нане­сены линии уровня этой поверхности. Процесс оптимиза­ции в этом случае проходит следующим образом. Точкаописывает начальное приближение. Проводя спуск по координате, попадем в точку. Далее, двигаясь параллельно оси ординат, придем в точку, и т. д.

Важным здесь является вопрос о сходимости рассматриваемого процесса оптимизации. Другими словами, бу­дет ли последовательность значений целевой функции сходиться к наименьшему ее значению в данной области? Это зависит от вида самой функции и выбора начального прибли­жения.

Для функции двух пере­менных очевидно, что метод неприменим в случае нали­чия изломов в линиях уров­ня. Это соответствует так на­зываемому оврагу на поверх­ности. Здесь возможен слу­чай, когда спуск по одной координате приводит, на «дно» оврага. Тогда любое движение вдоль другой коор­динаты ведет к возрастанию функции, соответствующему подъему на «берег» оврага. Поскольку поверхности типа «оврага» встречаются в инже­нерной практике, то при использовании метода покоор­динатного спуска следует убе­диться, что решаемая зада­ча не имеет этого недостатка. Для гладких функций при удачно выбранном началь­ном приближении (в некото­рой окрестности минимума) процесс сходится к миниму­му. К достоинствам метода покоординатного спуска сле­дует также отнести возможность использования простых алгоритмов одномерной оптимизации. Блок-схема метода покоординатного спуска представлена на рисунке.