Использование сплайнов.

Одним из методов численного интегрирования, особенно эффективным при строго ограниченном числе узлов, является метод сплайнов, использующий интерполяцию сплайнами.

Разобьем отрезок интегрирования начастей точками. Пусть. На каж­дом элементарном отрезке интерполируем подынтеграль­ную функциюс помощью кубического сплайна:(1).

Выражение для интеграла представим в виде .

Используя выражение (1), в результате вычисления интегралов находим (2).

Для практических расчетов формулу (2) можно представить в виде (3).

Анализ этой формулы показывает, что первый член в правой части совпадает с правой частью формулы для метода трапеций. Следовательно, второй член харак­теризует поправку к методу трапеций, которую дает ис­пользование сплайнов.

Как следует из формулы (1), коэффициенты выражаются через вторые производные:

.

Это позволяет оценить второй член правой части фор­мулы (3):

,

где - вторая производная в некоторой внутренней точке. Полученная оценка показывает, что добавка к фор­муле трапеций, которую дает использование сплайнов, компенсирует погрешность самой формулы трапеций.

Отметим, что во всех предыдущих методах формулы численного интегрирования можно условно записать в виде линейной комбинации табличных зна­чений функции:

.

При использовании сплайнов такое представление не­возможно, поскольку сами коэффициенты зависят от всех значений.

Рассмотрев разные методы численного интегрирова­ния, трудно сравнивать их достоинства и недостатки. Любая попытка такого сравнения непременно поставит перед нами альтернативный вопрос: что больше, или? Все зависит от самой функциии поведения ее производных.

Уточнение результатов численного интегрирования можно проводить по-разному. В частности, в представленном на рисунке алгоритме с использованием метода Симпсона проводится сравнение двух значений интеграла и, полученных при разбиениях отрезкасоот­ветственно с шагамии. Аналогичный алгоритм можно построить и для других методов.

Здесь мы упомянем другую схему уточнения значе­ния интеграла - процесс Эйткена. Он дает возможность оценить погрешность метода и указывает алгоритм уточнения результатов. Расчет проводится последователь­но три раза при различных шагах разбиения, причем их отношения постоянны:

(на­пример, при делении шага пополам ). Пусть в результате численного интегрирования получены значе­ния интеграла. Тогда уточненное значение ин­теграла вычисляется по формуле:

,

а порядок точности используемого метода численного интегрирования определяется соотношением .

Уточнение значения интеграла можно также проводить методом Рунге — Ромберга .

Адаптивные алгоритмы.

Из анализа погрешностей методов численного интегрирования следует, что точность получаемых результатов зависит как от характера изме­нения подынтегральной функции, так и от шага интегри­рования. Будем считать, что величину шага мы задаем. При этом ясно, что для достижения сравнимой точности при интегрировании слабо меняющейся функции шаг можно выбирать большим, чем при интегрировании рез­ко меняющихся функций.

На практике нередко встречаются случаи, когда подынтегральная функция меняется по-разному на от­дельных участках отрезка интегрирования. Это обстоя­тельство требует такой организации экономичных чис­ленных алгоритмов, при которой они автоматически при­спосабливались бы к характеру изменения функции. Та­кие алгоритмы называются адаптивными (приспосабли­вающимися). Они позволяют вводить разные значения шага интегрирования на отдельных участках отрезка интегрирования. Это дает возможность уменьшить ма­шинное время без потери точности результатов расчета. Подчеркнем, что этот подход используется обычно при задании подынтегральной функции в виде фор­мулы, а не в табличном виде.

Программа, реализующая адаптивный алгоритм численного интегрирования, входит обычно в виде стандартной подпрограммы в математическое обеспечение ЭВМ. Пользователь готовой программы задает границы отрезка интегрирования , допустимую абсолютную погреш­ностьи составляет блок программы для вычисления значения подынтегральной функции. Программа вычисляет значение интегралас заданной погреш­ностью, т. е.

(4).

Разумеется, не для всякой функции можно получить результат с заданной погрешностью. Поэтому в програм­ме может быть предусмотрено сообщение пользователю о недостижимости заданной погрешности. Интеграл при этом вычисляется с максимально возможной точностью, и программа выдает эту реальную точность.

Рассмотрим принцип работы адаптивного алгоритма. Первоначально отрезок разбиваем начастей. В дальнейшем каждый такой элементарный отрезок де­лим последовательно пополам. Окончательное число ша­гов, их расположение и размеры зависят от подынте­гральной функции и допустимой погрешности каждому элементарному отрезкуприме­няем формулы численного интегрирования при двух различных его разбиениях. Получаем приближениядля интеграла по этому отрезку:

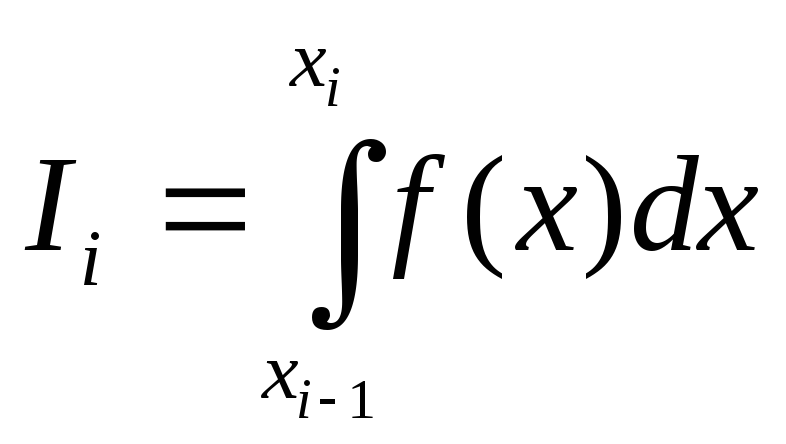(5).

Полученные значения сравниваем и проводим оценку их погрешности. Если погрешность находится в допустимых границах, то одно из этих приближений принимается за значение интеграла по этому элементарному отрезку. В противном случае происходит дальнейшее деление от­резка и вычисление новых приближений. С целью эко­номии машинного времени точки деления располагаются таким образом, чтобы использовались вычисленные зна­чения функции в точках предыдущего разбиения.

Например, при вычислении интеграла (5) по формуле Симпсона отрезок сначала разбиваем на две части с шагоми вычисляем значение. Потом вычисляемс шагом. Получим выражения

(6),

(7).

Формулу (7) можно также получить двукратным при­менением формулы (6) для отрезков и.

Процесс деления отрезка пополам и вычисления уточненных значений ипродолжается до тех пор, пока их разность станет не больше некоторой заданной величины, зависящей оти:

(8).

Аналогичная процедура проводится для всех элементарных отрезков. Величинапринимается в качестве искомого значения интеграла. Условия (8) и соответствующий выбор величинобеспечивают вы­полнение условия (4).

О других методах.Особые случаи.

Кроме рассмот­ренных выше методов численного интегрирования су­ществует ряд других. Дадим краткий обзор некоторых из них.

Формулы Ньютона -Котесаполучаются путем заме­ны подынтегральной функции интерполяционным мно­гочленом Лагранжа с разбиением отрезка интегрирова­ния наравных частей. Получающиеся формулы ис­пользуют значения подынтегральной функции в узлах интерполяции и являются точными для всех многочленов некоторой степени, зависящей от числа узлов.(Точность формул растет с увеличением степени интерполяцион­ного многочлена).

Метод Гауссане предполагает разбиения отрезка ин­тегрирования на равные промежутки. Формулы числен­ного интегрирования интерполяционного типа ищутся такими , чтобы они обладали наивысшим порядком точно­сти при заданном числе узлов. Узлы и коэффициенты формул численного интегрирования находятся из усло­вий обращения в нуль их остаточных членов для всех многочленов максимально высокой степени.

Формула Эрмита, являющаяся частным случаем формул Гаусса, использует многочлены Чебышева для вычисления интегралов вида.

Получающаяся формула характерна тем, что все коэффициенты при равны.

Метод Марковасостоит в том, что при выводе формул Гаусса вводятся дополнительные предположения о совпадении точек разбиения отрезка, по крайней мере, с одним из его концов.

Формула Чебышевапредставляет интеграл в виде

При этом решается следующая задача: найти точки и коэффициенттакие, при которых остаточный членобращается в нуль, когда функцияявляется произвольным многочленом возможно большей степени.

Формула Эйлераиспользует не только значения подынтегральной функции в точках разбиения, но и ее производные до некоторого порядка на границах отрезка.

Рассмотрим особые случаи численного интегрирова­ния: а) подынтегральная функция разрывна на отрезке интегрирования; б) несобственные интегралы.

а) В ряде случаев подынтегральная функция или ее производные в некоторых внутренних точкахотрезка интегрированиятерпят раз­рыв. В этом случае интеграл вычисляют численно каждого участка непрерывности и результаты складывают. Например, в случае одной точки разрываимеем

.

Для вычисления каждого из стоящих в правой части ин­тегралов можно использовать рассмотренные выше ме­тоды.

б) Не так просто обстоит дело с вычислением несоб­ственных интегралов. Напомним, что к такому типу от­носятся интегралы, которые имеют хотя бы одну бес­конечную границу интегрирования или подынтеграль­ную функцию, обращающуюся в бесконечность хотя бы в одной точке отрезка интегрирования.

Рассмотрим сначала интеграл с бесконечной границей интегрирования, например интеграл вида

,.

Существует несколько приемов вычисления таких инте­гралов.

Можно попытаться ввести замену переменных , которая превращает интервал интегрирова­нияв отрезок. При этом подынтегральная функция и первые ее производные до некоторого поряд­ка должны оставаться ограниченными.

Еще один прием состоит в том, что бесконечная гра­ница заменяется некоторым достаточно большим числом так, чтобы принятое значение интеграла отличалось от исходного на некоторый малый остаток, т. е.

,.

Если функция обращается в бесконечность в некото­рой точке конечного отрезка интегрирования, то можно попытаться выделить особенность, представив подынтегральную функцию в виде суммы двух функций:

.

При этом ограничена, аимеет особенность в данной точке, но интеграл (несоб­ственный) от нее может быть вычислен непосредственно по формулам. Тогда численный метод используется толь­ко для интегрирования ограниченной функции.