Лекция 5.

На практике формулой Ньютона-Лейбница часто нельзя воспользоваться по двум основным причинам: * вид функции не допускает непосредственного интегрирования, т. е. первообразную нельзя выразить в элементарных функциях; *значения функции заданы только на фиксированном конечном множестве точек , т.е. функция задана в виде таблицы.

В этих случаях используются методы численного интегрирования. Они основаны на аппроксимации подынтегральной функции некоторыми более простыми выражениями, например многочленами.

В первом случае подынтеграль­ную функцию можно представить в виде степенного ряда (ряда Тейлора). Это позволяет свести вычисление интеграла от сложной функции к интегрированию многочлена, представляющего первые несколько членов ряда.

Пример. Вычислить интеграл с погрешностью .

.

Заменяя на : .

Более универсальными методами, которые пригодны для обоих слу­чаев, являются методы численного интегрирования, основанные на ап­проксимации подынтегральной функции с помощью интерполяционных многочленов. Будем использовать кусочную (локальную) интерполяцию. Это позволит приближенно заменить приближенный интеграл интегральной суммой. В зависимости от способа ее вычисления получаются разные методы численного интегрирования (методы прямоугольников, трапеций, парабол, сплайнов и д.р.).

Методы прямоугольников и трапеций.

Простейшим методом численной интерполяции является метод прямоугольников. Он использует замену определенного интеграла интегральной суммой

.

В качестве точек могут выбираться левые или правые границы элементарных отрезков. Обозначая , , получаем формулы метода прямоугольников

.

Более точным является вид формулы прямоугольников, использующий значения функции в средних точках элементарных отрезков (в полуцелых узлах):

, .

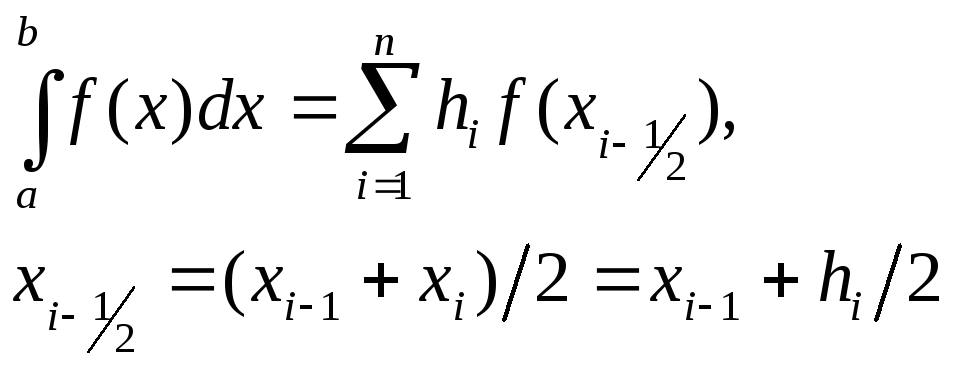В дальнейшем под методом прямоугольников будем понимать последний алгоритм (метод средних).

Метод трапеций использует линейную интерполяцию, т.е. график функ­ции представляется в виде ломаной, соединяющей точ­ки . В этом случае площадь всей фигуры (криволинейной трапеции) складывается из площадей элементарных прямолинейных трапеций.

Площадь каждой такой гранении равна произведению полусуммы оснований на высоту:

.

Складывая все эти равенства, получаем фор­мулу трапеций для численного интегрирова­ния:

.

При интегрировании с постоянным шагом :

- (метод средних).

- формула трапеций.

Метод Симпсона.

Разобьем отрезок интегрирования на четное число равных частей с шагом . На каж­дом отрезке подынтегральную функцию заменим интерполяционным многочленом вто­рой степени:

.

Коэффициенты этих квадратных трехчленов мо­гут быть найдены из условий равенства много­члена в точках соответствующим табличным данным .В качестве можно принять ин­терполяционный многочлен Лагранжа второй степени, проходящий через точки , : .

Элементарная площадь может быть вычис­лена с помощью определенного интеграла. Учитывая равенства , получаем . Проведя такие вычисления для каждого элементарного отрезка , просуммируем полученные выражения:

- формула Симпсона.

Блок-схема одного из простейших алгоритмов вычисления определенного интеграла по методу Симпсона представлена на рисунке. В качестве исходных данных задаются границы отрезка интегрирования , погрешность , а также формула для вычисления значений подынтегральной функции . Первоначально от­резок разбивается на четыре части с шагом . Вычисляется значение интеграла. Потом число шагов удваивается, вычисляется значение с ша­гом . Условие окончания счета принимается в виде . Если это условие не выполнено, происходит новое деление шага пополам и т.д.

Отметим, что представленный на рисунке алгоритм не является оптимальным. В частности, при вычислении каждого последующего приближения не используются значения функции , уже найденные на предыдущем этапе.