Мат. логика

26.Понятие формулы логики предикатов. Значение формулы логики предикатов.

1.Символами p, q, r договоримся обозначать переменные высказывания, каждый из которых принимает либо 0, либо 1.

2.Через x, y, z – предметные переменные, которые берут свои значения из некоторого множества М

3.x0, y0, z0 – предметные константы

Р(-), F(-)- одноместные предикатные переменные.

Q(-, …, -), R(-, …, -) – n-местные предикатные переменные P0(-), Q0(-, …,-) – символы постоянных переменных

4.-, *, +, → - символы логических операций

5.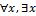 - символы кванторных операций

6.(, ), , -вспомогательные символы

Сучетом введенной символики формула ЛП примет вид:

1.Каждое высказывание, как переменное, так и постоянное, является формулой.

2.Если F(-, …, -) – n-местная предикатная переменная или постоянный предикат, а х1, х2, …, хn

– предметные переменные или предметные постоянные (необязательно все различимые), то

выражение вида F(х1, х2, …, хn) – формула или элементарная формула.

ВF(х1, х2, …, хn) предметные переменные – свободные.

3.Если А и В – формулы, при чем такие, что одна и та же предметная переменная не является в одной из них связанной, а в другой свободной, то слова А+В, АВ, А→В – формулы.

4.Если А – формула, то - формула.

5.Если А(х) – формула, в которую предметная переменная х входит свободно, то слова 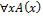и являются формулами, при чем предметные переменные в них уже

связаны. Пример:

Предположим, что мы располагаем P(x), Q(x,y), q, r, тогда формулами будут q, P(x), P(x)*Q(x0,y),

→

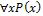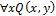→P(x) – формулой не является. Всякая формула АВ является и формулой ЛП.

Значение формулы логики предикатов

Значение формулы логики предикатов зависит от значения трех видов переменных:

a)От переменных высказываний

b)От свободных предметных переменных

c)От предикатных переменных

Пример:

Пусть требуется вычислить (1)

Рассмотрим эту формулу, в которой двухместный предикат определен на множестве М*М, где М={0,1,2,…,n}.

Вформулу (1) входит переменный предикат Р(х, у), предметные переменные х, у, z, при чем y, z – связанные, х - свободный.

Вкачестве конкретного значения предикатной переменной Р(х, у) возьмем фиксированный предикат Р0(х, у), «x < y».

Свободной переменной х подставим х0=5. Получим 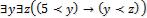=1.

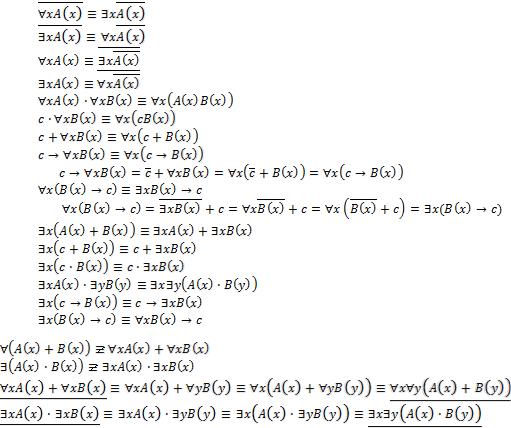
27. Равносильные формулы логики предикатов.

Две формулы логики предикатов А и В называются равносильными на области М, если они принимают одинаковые логические значения при всех значениях, входящих в них переменных.

Две формулы логики предикатов А и В называются равносильными, если они равносильны во всякой области.

Ясно, что все равносильности алгебры высказываний будут верны, если в них, вместо переменных высказываний подставить произвольные формулы ЛП.

Имеют место равносильности и самой ЛП. Рассмотрим основные из них.

Обозначим А(х), В(х) – переменные предикаты, С – переменные высказывания. Тогда имеет место 15 равносильностей ЛП:

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

Замечание:

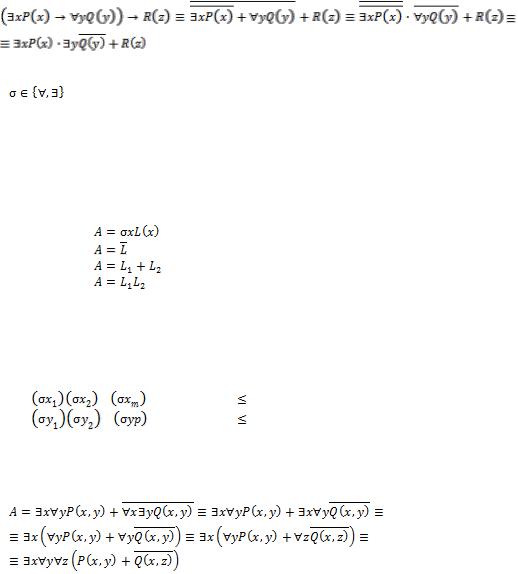
28. Предварённая нормальная форма.

Формула ЛП имеет нормальную форму, если она содержит только операции конъюнкции, дизъюнкции и кванторные операции, а операция отрицания отнесена к элементарным формулам.

Используя равносильности АВ и ЛП, каждую формулу ЛП можно привести к нормальной форме.

Предваренная нормальная форма (ПНФ) имеет следующий вид 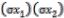… А(х1, х2, …, хm), n 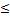m

Формула А кванторов не содержит.

Теорема: Всякая формула логики предикатов может быть приведена к ПНФ. Доказательство:

Будем исходить из того, что формула А уже приведена к нормальной форме и покажем, что ее можно привести к ПНФ.

1.Если данная формула является элементарной, то она кванторов не содержит и, следовательно, уже представлена в ПНФ.

2.Предположим, что теорема справедлива для формул L(х), L1(х1, х2, …, хn), L2(х1, х2, …, хq) Формула А может быть образована одним из четырех способов.

1)

2)

3)

4)

1)У L(x) все кванторные операции стоят впереди, но тогда, формула уже записана в ПНФ.

2). Формула L записана в ПНФ, но тогда, с помощью равносильностей 1 и 2 отрицание можно ввести под знак кванторов и это приведет формулу А к ПНФ.

3)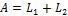. Переименуем в формуле L2 предметные переменные х1, х2, …, хq так, чтобы в формулах L1 и L2 все предметные переменные были различны.

Тогда L1 и L2 можно записать так:

Используя 7 и 11 равносильности формулу А можно записать:

А1 = …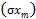(B1(х1, х2, …, хn) + …B2(y1, y2, …, yq)).

4)Доказательство аналогично пункту 3), при этом используются равносильности 6 и 12.

Пример: Привести к ПНФ следующую формулу:

29. Общезначимость и выполнимость формул логики предикатов.

Определение. Формула А ЛП называется выполнимой в области М, если существуют значения переменных из этой области при которых формула А принимает истинные значения.

Определение. Формула А называется выполнимой, если существует область, на которой эта формула выполняется.

Определение. Формула А называется тождественно истинной в области М, если она принимает истинные значения для всех значений переменных, входящих в эту формулу и отнесенных к этой области.

Определение. Формула А называется общезначимой, если она тождественно истинная на всякой области.

Определение. Формула А называется тождественно ложной в области М, если она принимает ложные значения для всех значений переменных, входящих в эту формулу и отнесенных к этой области.

Примеры:

значит она выполнима.

Если рассмотреть предикат «x < y» М1= Е1*Е1, Е1 = {0, 1, 2,…, k}, тогда эта формула тождественно ложна в М1 и, следовательно, не выполнима в М1. Тогда начальная формула не общезначима.

2. - выполнима.

Если взять Р0(х): «число х – четное» М = Е, Е = {0, 1, 2,…, n,…}

Эта формула тождественно истинная в области М, следовательно, выполнима в области М.

Если предикат Р0(х) рассматривать на области М1=Е1, Е1 – множество только четных чисел. Тогда тождественно ложная в области М1 и, следовательно, не выполнима.

3. - эта формула тождественно истинна в любой области, следовательно,

общезначима, и, значит, является логическим законом, закон исключительного третьего в ЛП.

4. - это формула тождественно ложная в любой области М, и, значит, она не выполнима.

Пример формулы, выполнимой в бесконечной области и невыполнимой ни в какой конечной области:

(1)

Предположим, что формула (1) выполнима в некоторой области М, тогда должен существовать предикат Р0(х, у), для которого формула (1) примет значение 1. Это значит, что для всех x, y, z и хотя бы для одного элемента u из области М формула

= 1

= 1 (2)

(3)

(4)

Из (2) и (3) следует, что предикат 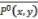удовлетворяет аксиомам порядка

1)

Условия выражать словами: «х предшествует у».

Из истинности формулы (4) следует, что для каждого z должно существовать такое u, что истинным

является : «z предшествует u».

Возьмем произвольный элемент х1, тогда найдем х2, такой, что х1 предшествует х2. Для х2, должны найтись х3, для которых х2 предшествует х3. Получим: х1, х2, …, хn (5). В силу аксиом все элементы различные, это и означает, что последовательность бесконечна, то и множество М бесконечно.

Если же М конечно, то формула (1) ложна на М, а значит, не выполнима.

30.Проблема разрешимости для общезначимости и выполнимости применительно к логике предикатов.

Проблемы разрешимости для общезначимости и выполнимости в общем случае

Эта проблема применительно к логике предикатов формулируется так: Существует ли алгоритм, позволяющий за конечное число шагов для любой формулы А ЛП установить, является ли она общезначимой, выполнимой или противоречивой.

В 1936 г. американский математик Черч доказал, что проблема разрешимости логики предикатов в общем виде алгоритмически не разрешима.

Алгоритмы распознавания общезначимости формул в частных случаях

1.Проблемы разрешимости в случае конечных областей.

Эта проблема в случае конечных областей разрешима.

Действительно, в этом случае кванторные операции можно заменить операциями конъюнкции и

дизъюнкции, и тем самым свести формулу ЛП к формуле алгебры логики, для которой проблема разрешимости разрешима.

Пример:

M = {a, b}

2.Проблемы разрешимости для формул, содержащих в предваренной нормальной форме кванторы одного типа.

Если формула ЛП С содержит свободные переменные х1, х2, …, хn, то формула вида

называется замыканием общности формулы С. А формула

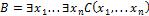называется замыканием существования формулы С. Следующая теорема гласит:

Теорема: Если замкнутая формула ЛП в ПНФ содержит только кванторы существования, число которых равно n и тождественно истинна на любой области, состоящей из одного элемента, то она общезначима.

Доказательство: Пусть эта формула имеет следующий вид:

(1), где

С кванторов не содержит, q1 – это логические переменные, пропозициональные, Pi – это одноместные предикаты, Qi – двухместные предикаты.

По условию теоремы, на любой области M={a} данная формула тождественно истинна, то есть

= 1 (2)

Формула (2) является формулой АЛ.

Предположим, что формула (1) не является общезначимой, тогда существует такая предметная область М1 и набор значений переменных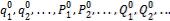

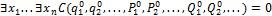(3)

Если взять отрицание (3), то:

=>

(4), независимо от выбора предметных переменных из

области М1.

Возьмем из области М1 какой-нибудь один элемент и обозначим его через а и подставим его в (4).

, что противоречит (2), поэтому наше предположение не верно. Поэтому (1) общезначима

.

3.Теорема: Если замкнутая формула логики предикатов в ПНФ содержит только кванторы общности, число которых равно m и тождественно истинна на всяком множестве, содержащем не более, чем n элементов, то она общезначима.

Доказательство: Пусть формула имеет следующий вид:

(1)

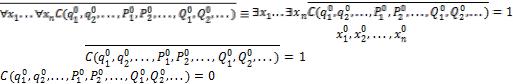
Предположим, что формула (1) не общезначима, тогда существует предметная область М1 с числом элементов больше n, на которой (1) не является тождественной истинной, то есть существует набор

значений переменных , на котором

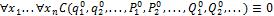(2)

, а это означает, что из области М1 можно выделить область М2, содержащую не более n элементов, на которых данная формула не является тождественно истинной, а это противоречит условию теоремы.

31. Метод аналитических таблиц.

Идея метода состоит в том, что тезис об общезначимости формулы А и тезис о следовании

формулы В из обосновываются методом от противного.

Рассуждение от противного оформляется в виде последовательности шагов, которые образуют аналитическую таблицу. Каждому шагу рассуждения соответствует определенная строка таблицы. Любая строка таблицы содержит один или несколько списков формул, разделяемых вертикальными линиями. Наличие формулы С в некотором списке истолковывается как утверждение об истинности С,

аналичие – как утверждение о ложности формулы С.

Первая строка таблицы содержит один список формул (антитезис): – допущение о ложности А

(тезис ) либо 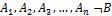– допущение об истинности 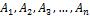и ложности B

(тезис ).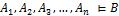

Переход от i-той строки (i=1,2, …) к i+1-ой осуществляется с помощью правил редукции (сведения к более простому, доступному для анализа или решения).

Цель рассуждения от противного – показать, что исходные допущения (антитезис) приводит к противоречию. То есть получению такой строки, каждый список формул которой содержит формулу

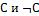. При получении данного результата тезисы или считаются обоснованными и построение таблицы завершается.

Правила редукции

[*] Предположим, что i-я строка содержит список формул следующего вида

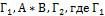– часть списка (возможно пустая), предшествующая А*В, а – часть списка (возможно пустая), следующая за А*В.

сохранив при этом все другие списки формул i-ой строки. Сокращенно:

Правило . Предварительные сведения:

1. n-местные предметно-функциональные константы (n>=1) – n-местные функции:

2.Определение терма:

a.Произвольная предметная константа является термом;

b.Произвольная предметная переменная является термом;

c.Если Ф-n-местная предметно-функциональная константа, а t1, t2, …, tn – термы, то Ф(t1, t2, …, tn) – терм;

d.Ничто иное не является термом.

Примеры:

1.a1, b1, c3

2.x2, y, z10

3.f1(g2(x,a)), f(g(x,a)) (часто верхние индексы опускаются)

4.h2(g2(x,a)) – не терм

5.Р1(g(x,a)) – не терм

3.Замкнутые термы:

Терм, не содержащий в своем составе предметных переменных, называется замкнутым.

Где t – произвольный замкнутый терм.

Пояснение: В случае истинности истинной оказывается любая формула вида А(t), которая есть результат замены всех свободных вхождений х в А на произвольный замкнутый терм t.

Формула xA(x) сохраняется в новом списке, чтобы в процессе дальнейшего построения аналитической таблицы можно было бы повторным применением данного правила получать утверждения об истинности А(t1), А(t2),… для термов, отличных от терма t.

Рекомендации по выбору терма t: в качестве t следует выбирать замкнутый терм из числа тех, которые уже содержатся в формулах данного списка.

Правило [¬ ].

,

где А(k) – результат замены всех свободных вхождений переменной х в формуле А на предметную константу k, которая не содержится в верхнем списке формул. Смысл этого ограничения следующий: если k входит в формулы указанного списка, то не исключается возможность, что эти формулы содержат информацию об истинности А(k). Тогда делать вывод, что именно объект k не удовлетворяет условию А, было бы некорректно.

.

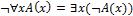Правило [ ].

, где A(k) то же, что и в предыдущем правиле.

Правило [ ].

, где А(t) то же, что и в правиле [].

Определение аналитической таблицы.

Аналитической таблицей называется конечная или бесконечная последовательность строк I1, I2,…, в которой каждая строка Ij содержит конечное число списков формул языка логики предикатов, а каждая последующая строка Ij+1 получается из предшествующей Ij заменой какого-нибудь списка формул на основе некоторого правила редукции.

Список формул называется замкнутым, если в его составе имеется некоторая формула С и её отрицание ¬ С.

Аналитическая таблица называется замкнутой, если она содержит конечное число строк и каждый список формул, находящийся в последней строке таблицы, является замкнутым.

Таким образом, для обоснования тезисов А или А1,А2,…,Аn В необходимо построить соответствующие замкнутые аналитические таблицы.

Общие рекомендации:

1. При построении аналитической таблицы следует сначала применять пропозициональные правила:

[*], [¬ *], [+], [¬ +], [→], [¬ →], [¬ ¬], а затем кванторные: [], [], [], [].

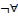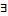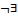2. Среди пропозициональных правил следует сначала применять правила: [*], [¬ +], [¬ →], [¬ ¬], которые не увеличивают число формульных списков в следующей строке таблицы, а затем правила: [¬ *], [+], [→]. В этом случае аналитическая таблица будет менее громоздкой.

3. Среди кванторных правил в первую очередь следует применять правила: [], [], 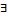которые

требуют введения новых предметных констант, и только потом правила [], [], не содержащие ограничений на терм t.

Пример 1. Обоснуем следующий тезис: P(a) + Q(b), Q(b) → R(c) R(c) + P(a)

P(a) + Q(b), Q(b) → R(c), ¬ (R(c) + P(a))

32. Силлогистика Аристотеля.

Всиллогистике Аристотеля используются только категорические суждения.

Категорическое суждение – суждение, в котором выражается знание о принадлежности или непринадлежности признака предмету, независимо от каких-либо условий».

Формально категорические суждения представляются в виде:

1.S есть (суть) P

2.S не есть (не суть) P

где S, P – термины или компоненты суждения, причем S – предмет мысли или субъект, а P – то, что говорится о субъекте, его свойство и предикат.

Примеры:

«Все птицы имеют перья», «этот котенок голоден», «свинец – тяжелый металл» S – «все птицы», «этот котенок», «свинец»

P – это правая часть предложения-предикат, она сообщает некоторые сведения об этих субъектах.

Аристотель рассматривал четыре основных вида категорических суждений: А – общеутвердительное: все S суть P

E – общеотрицательное: ни одно S не есть P

I – частноутвердительное: некоторые S суть P

O – частноотрицательные: некоторые S не суть P

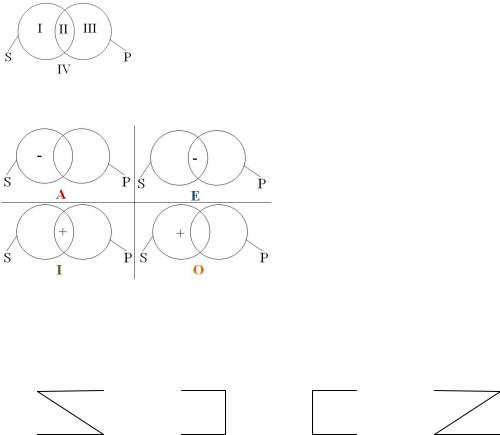
Наиболее просто, наглядно и строго силлогистику Аристотеля можно изложить с помощью кругов Эйлера. В любом из четырех категорических суждений как левый термин S, так и правый термин P определяют некоторые классы предметов. Отношение между этими классами в общем случае можно показать пересекающимися кругами Эйлера.

I – предметы принадлежат классу S, но не принадлежат классу P II – предметы принадлежат одновременно обоим классам

III – предметы принадлежат классу P, но не принадлежат классу S IV – предметы не принадлежат ни классу S, ни классу P

В силлогистике Аристотеля последний случай не исследуется.

Каждое конкретное суждение сообщает некоторую информацию либо об области I, либо II, либо III, причем S ≠ Ø и P ≠ Ø

Отмечаем пустоту области знаками минус (-), а непустоту – знаком плюс (+), представим суждения в более наглядной форме:

Основное содержание силлогистики связано с понятием силлогизма как умозаключения, в котором из двух категорических суждений (посылок) получается третье (заключение).

Общее число терминов в суждениях равно трем: один из них входит в обе посылки, называется средним и обозначается M (medius), а два других называемых крайними, переходят из посылок в заключение и обозначается через S (меньший термин) и P (больший термин) в соответствии с тем местом, которое они займут в заключении: S будет играть роль субъекта, а P – роль предиката.

В посылках термины M, S и P могут занимать любое место. Посылка с большим термином P называется большей и ставится на первое место. Посылка с меньшим термином S называется меньшей.

Возможны 4 варианта размещения терминов в посылках, которые принято называть фигурами силлогизма.