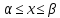- •Поверхностные интегралы
- •Составители: с.Н. Алексеенко
- •Предисловие
- •Определение направляющих косинусов нормами
- •Площадь поверхности
- •Сторона поверхности
- •Орентация поверхности.
- •Поверхностные интегралы первого типа
- •Поверхностные интегралы второго типа.
- •Формула остроградского-гаусса
- •Формула интегрирования по частям
- •Формула грина
- •Формула стокса
- •Литература
- •Задания
Формула остроградского-гаусса
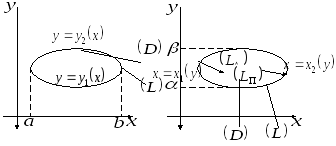
Рассмотрим
трехмерную пространственную область
 ,
ограниченную кусочно-гладкими
поверхностями
,
ограниченную кусочно-гладкими
поверхностями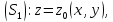
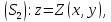 и цилиндрической поверхностью
и цилиндрической поверхностью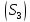 ,
образующие которой параллельны осиz.
,
образующие которой параллельны осиz.
Направляющей
поверхности
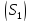 служит кусочно-гладкая замкнутая кривая
служит кусочно-гладкая замкнутая кривая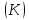 на плоскостиx0y,
ограничивающая плоскую область
на плоскостиx0y,
ограничивающая плоскую область
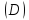 (
(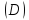 – проекция
– проекция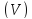 наx0y).
В частном случае на кривой
наx0y).
В частном случае на кривой
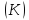 может выполняться и равенство
может выполняться и равенство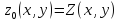 ,
тогда
,
тогда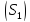 вырождается в линию.
вырождается в линию.
Допустим,
что в области
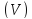 определена функция
определена функция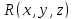 непрерывная вместе со своей производной
непрерывная вместе со своей производной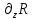 во всей
во всей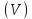 ,
включая ее границу. Имеем для тройного
интеграла в области
,
включая ее границу. Имеем для тройного
интеграла в области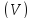 :
:
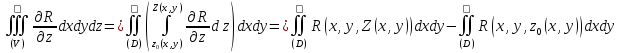
Если ввести в рассмотрение поверхностные интегралы, то в силу установленных формул:
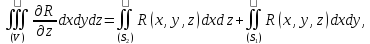
причем
первый из интегралов справа распространен
на верхнюю
сторону
поверхности
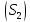 ,
а второй нанижнюю
сторону поверхность
,
а второй нанижнюю
сторону поверхность
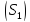 .
Равенство не нарушится, если мы прибавим
к правой части интеграл
.
Равенство не нарушится, если мы прибавим
к правой части интеграл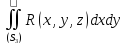 ,
распространенный навнешнюю
сторону поверхности
,
распространенный навнешнюю
сторону поверхности
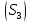 ,
так как он равен нулю.
,
так как он равен нулю.
Объединяя все поверхностные интегралы, получим формулу:
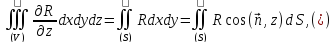
где
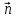 – внешняя нормаль к области
– внешняя нормаль к области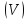 на ее поверхности.
на ее поверхности.
Эти формулы установлены нами лишь для цилиндрических брусов, определенным образом ориентированных. Но они верны и для гораздо более широкого класса тел, которые могут быть разложены на части изученного вида с помощью цилиндрических поверхностей с образующими, параллельным оси z. Действительно, осуществив это разложение, мы можем применить к каждой части формулу (*) и затем сложить результаты. Так как интегралы, распространенные на вспомогательные цилиндрические поверхности равны нулю, мы снова приходим к формуле (*).
Можно доказать, что (*) справедлива вообще для тел, ограниченных произвольными кусочно-гладкими поверхностями.
Аналогично (*) имеют место формулы:
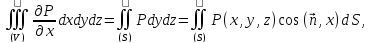
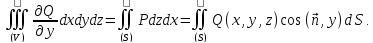
если
функции P
и
Q
непрерывны в области
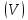 вместе со своими производными
вместе со своими производными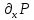 и
и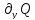 .
.
Сложив все три формулы, придем к формуле Остроградского-Гаусса:
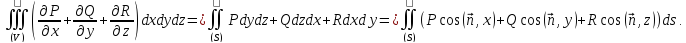
Взяв P=x, Q=y, R=z, получим три формулы для объема тела:
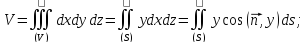
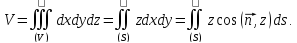
Сложив эти формулы, получим:
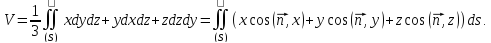
Формула интегрирования по частям
Переобозначим
координаты
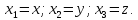 Для любых непрерывно дифференцируемых
функцийu
и
v
справедлива
формула:
Для любых непрерывно дифференцируемых
функцийu
и
v
справедлива
формула:
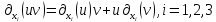 .
Отсюда следует
.
Отсюда следует
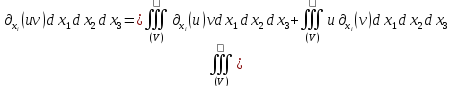 .
Обозначим также
.
Обозначим также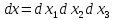 .
Пользуясь установленными ранее формулами,
получим
.
Пользуясь установленными ранее формулами,
получим

Пользуясь введенными обозначениями координат и введя так же обозначения:
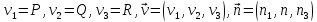
можем переписать формулу Остроградского-Гаусса в следующем виде:
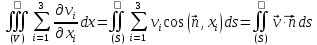
так
как
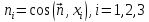 .
.
Формула грина
Пусть
в плоскости x0y
задана область
 ,
ограниченная замкнутым контуром
,
ограниченная замкнутым контуром .
Предположим, что прямые, параллельные
осямx
и
y
пересекают
этот контур не более чем в двух точках,
так что контур можно описать любым из
следующих двух способов:
.
Предположим, что прямые, параллельные
осямx
и
y
пересекают
этот контур не более чем в двух точках,
так что контур можно описать любым из
следующих двух способов:
|
|
|
|
| |
Пусть
в области
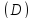 заданы функцииP
и Q,
непрерывные вместе со своими частными
производными первого порядка.
заданы функцииP
и Q,
непрерывные вместе со своими частными
производными первого порядка.
Рассмотрим
интеграл
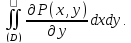
Представляя его в виде двукратного получим:
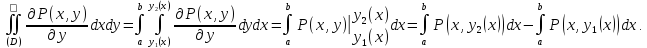
Интегралы
в правой части последнего выражения
являются криволинейными интегралами,
взятыми соответственно по верхней:
 и нижней
и нижней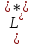 частям контура
частям контура .
Но только направление обхода контуров
у этих интегралов различное. Для того,
что бы у обоих интегралов было одно
направление обхода контура, переменим
в первом из них направление интегрирования.
.
Но только направление обхода контуров
у этих интегралов различное. Для того,
что бы у обоих интегралов было одно
направление обхода контура, переменим
в первом из них направление интегрирования.
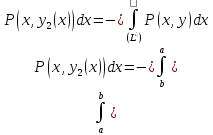 .
Отсюда следует:
.
Отсюда следует:
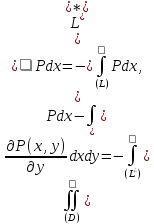
причем контур обходиться против часовой стрелки.
Аналогично
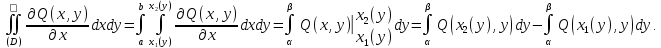
Здесь для сохранения правила обхода против часовой стрелки нужно изменить порядок интегрирования во втором интеграле справа. Тогда по аналогии получим:
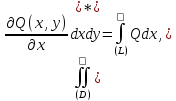
Вычитая (*) из (**) получим формулу Грина:
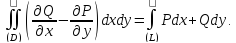
ЗАМЕЧАНИЕ. Каждая из формул (*) и (**) дает соответствующую формулу интегрирования по частям.
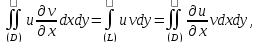
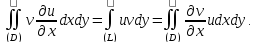

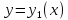 ,
,
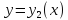 ,
,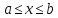
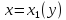 ,
x
,
x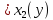 ,
,