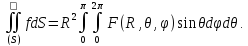- •Поверхностные интегралы
- •Составители: с.Н. Алексеенко
- •Предисловие
- •Определение направляющих косинусов нормами
- •Площадь поверхности
- •Сторона поверхности
- •Орентация поверхности.
- •Поверхностные интегралы первого типа
- •Поверхностные интегралы второго типа.
- •Формула остроградского-гаусса
- •Формула интегрирования по частям
- •Формула грина
- •Формула стокса
- •Литература
- •Задания
Поверхностные интегралы первого типа
Пусть
 - некоторая двусторонняя гладкая (или
кусочно – гладкая) поверхность,
ограниченная кусочно – гладким контуром.
Пусть на этой поверхности (т.е. в каждой
точке поверхности) определена функция
- некоторая двусторонняя гладкая (или
кусочно – гладкая) поверхность,
ограниченная кусочно – гладким контуром.
Пусть на этой поверхности (т.е. в каждой
точке поверхности) определена функция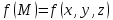 .Разобьём
поверхность
.Разобьём
поверхность
 с помощью сети произвольно проведённых
кусочно-гладких кривых на части
с помощью сети произвольно проведённых
кусочно-гладких кривых на части ,…,
,…,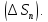 Выбрав в каждой части
Выбрав в каждой части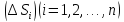 произвольным образом одну точку
произвольным образом одну точку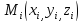 ,
вычислим в этой точке значение функции
,
вычислим в этой точке значение функции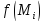 =
=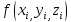 и умножив его на площадь
и умножив его на площадь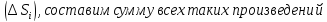
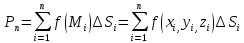 ,
,
которая называется интегральной суммой.
ОПРЕДЕЛЕНИЕ:
Конечный предел этой интегральной
суммы при бесконечном уплотнении
разбиения поверхности
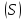 ,
не зависящий ни от способа разбиения
поверхности
,
не зависящий ни от способа разбиения
поверхности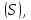 ни от выбора точек
ни от выбора точек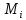 в
пределах каждой части
в
пределах каждой части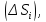 называется поверхностным интегралом
первого типа от функции
называется поверхностным интегралом
первого типа от функции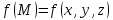 по поверхности
по поверхности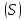 и обозначается символом
и обозначается символом
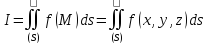 ,
, т.е.
т.е.
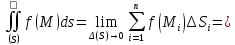
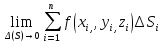 .
.
ТЕОРЕМА.
Пусть имеется незамкнутая гладкая
поверхность
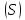 заданная явным уравнением
заданная явным уравнением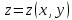 .
Положим, что прямые, параллельные оси
.
Положим, что прямые, параллельные оси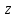 пересекают поверхность
пересекают поверхность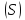 ,
не более чем в одной точке, и пусть
,
не более чем в одной точке, и пусть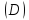 проекция
проекция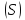 на плоскость
на плоскость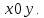
Тогда,
какова бы не была функция
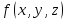 ,
определённая в точках поверхности
,
определённая в точках поверхности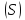 и ограниченная:
и ограниченная: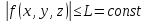 ,
имеет место равенство
,
имеет место равенство
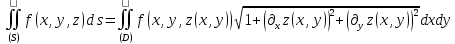
в предположении существования одного из этих интегралов (что влечет за собой и существование второго).
ЗАМЕЧАНИЕ.
Так как
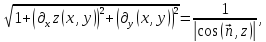 то формулу (*) можно записать и так:
то формулу (*) можно записать и так: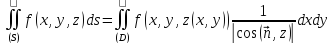 .
.
Доказательство
теоремы. Разложим
поверхность
 на части
на части ,
,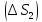 ,…,
,…,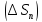 с помощью сети произвольно проведённых
кусочно – гладких кривых. Спроектируем
линии разбиения на плоскость
с помощью сети произвольно проведённых
кусочно – гладких кривых. Спроектируем
линии разбиения на плоскость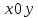 и получим соответствующее расположение
области
и получим соответствующее расположение
области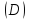 :
: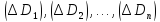 .
Между построенными разложениями областей
.
Между построенными разложениями областей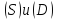 имеется то соответствие, что если к нулю
стремятся диаметры частей
имеется то соответствие, что если к нулю
стремятся диаметры частей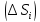 ,
то к нулю стремятся диаметры частей
,
то к нулю стремятся диаметры частей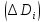 инаоборот.
Выберем в каждой части
инаоборот.
Выберем в каждой части
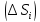 точку
точку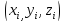 и составим интегральную сумму
и составим интегральную сумму
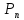 =
=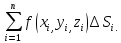 По определению
По определению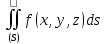 =
=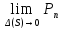 .
.
В силу общей формулы для площади поверхности
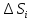 =
=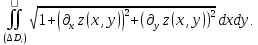
Обозначим
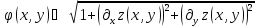 ,
то есть
,
то есть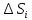 =
=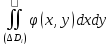 .
.
По
теореме о среднем,
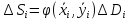 ,
где
,
где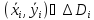 ,
[
,
[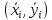 - не произвольные, а фиксированные точки,
определяемые теоремой о среднем].
- не произвольные, а фиксированные точки,
определяемые теоремой о среднем].
В
результате получим
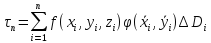 .
Интегральная сумма
.
Интегральная сумма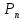 отличается от интегральной суммы для
интеграла
отличается от интегральной суммы для
интеграла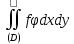 :
:
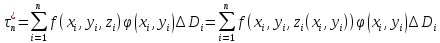 тем,
что в
тем,
что в
 значения
значения произвольно в пределах
произвольно в пределах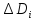 ,
а в
,
а в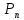 значения аргумента функции
значения аргумента функции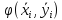 фиксировано теоремой о среднем.
фиксировано теоремой о среднем.
Рассмотрим
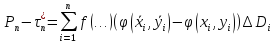 .
Пусть
.
Пусть
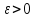 – произвольно малое число. В силу
равномерной непрерывности функции
– произвольно малое число. В силу
равномерной непрерывности функции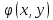 при достаточно малых диаметрах областей
при достаточно малых диаметрах областей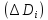 будет
будет
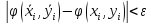 .
Отсюда
следует, что
.
Отсюда
следует, что
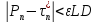 ,
то есть
,
то есть
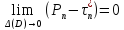 .
Так что
.
Так что
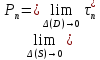 .
.
Это значит, что из существования одного предела следует существование другого и обратно. По определению это означает, что
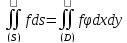 ,
что и т. д.
,
что и т. д.
ЗАМЕЧАНИЕ В частности двойной интеграл
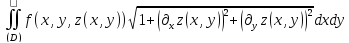 существует
в предложении непрерывности
существует
в предложении непрерывности
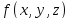 .
Напомним, что непрерывность функций
.
Напомним, что непрерывность функций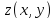 ,
,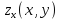 ,
,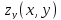 предполагалось при определении
поверхности (только тогда эта функция
обозначалась как
предполагалось при определении
поверхности (только тогда эта функция
обозначалась как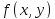 ).
).
ЗАМЕЧАНИЕ
Если
 или близок к нулю, или по каким-либо
другим причинам, поверхностный интеграл
первого типа можно с равным успехом
выразить через проекции на другие
координатные плоскости.
или близок к нулю, или по каким-либо
другим причинам, поверхностный интеграл
первого типа можно с равным успехом
выразить через проекции на другие
координатные плоскости.
Именно,
если
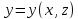 ,
то
,
то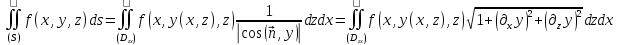 .
.
Или
если
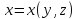 ,
то
,
то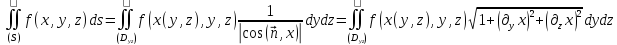 .
.
СЛЕДСТВИЕ
1.
Если
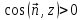 ,
то для любой непрерывной ограниченной
функции
,
то для любой непрерывной ограниченной
функции будет справедливо равенство
будет справедливо равенство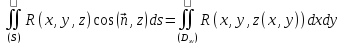 .
.
Если
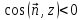 ,
то
,
то
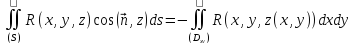 .
.
Если
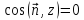 ,
то
,
то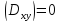 ,
поэтому эти равенства справедливы и в
этом случае.
,
поэтому эти равенства справедливы и в
этом случае.
Доказательство.
В
основной формуле
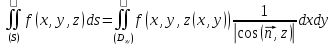
возьмём
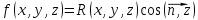 .
.
СЛЕДСТВИЕ
2.
Если
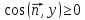 ,
то для любой непрерывной ограниченной
функции
,
то для любой непрерывной ограниченной
функции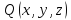 будет справедливо равенство
будет справедливо равенство
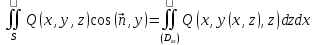
Если
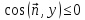 ,
то
,
то
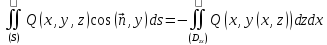 .
.
СЛЕДСТВИЕ
3.
Если
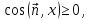 то для любой непрерывной ограниченной
функции
то для любой непрерывной ограниченной
функции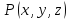 будет
справедливо равенство
будет
справедливо равенство
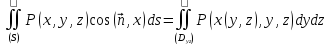 .
.
Если
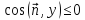 ,
то
,
то
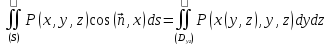 .
.
ЗАМЕЧАНИЕ. В задачах математической физики часто возникает необходимость выразить поверхностный интеграл первого типа
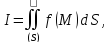
взятый
по поверхности сферы радиуса
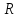 в сферических координатах. Выведем
соответствующую формулу. Рассмотрим
отдельно верхнюю и нижнюю часть сферы.
Они выражаются явной формулой:
в сферических координатах. Выведем
соответствующую формулу. Рассмотрим
отдельно верхнюю и нижнюю часть сферы.
Они выражаются явной формулой:
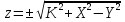
Пусть
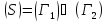
По
формуле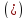
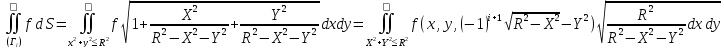 ,
,
 .
.
На плоскости введем координаты:
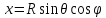 ,
,
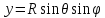 ,
,
(т.е. точка на плоскости рассматриваемая как проекция точки на сфере), и произведем замену переменных интегрирования.
Якобиан перехода

Кроме того
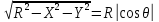
Для
верхней половины
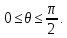
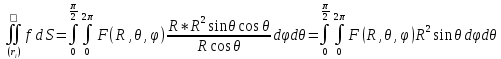 .
.
Для нижней половины с учетом того, что якобиан берется по абсолютной величине
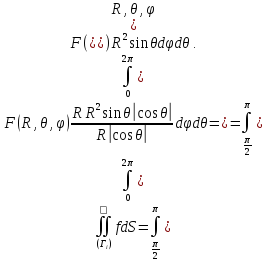
Складывая, получаем требуемую формулу: