3.5.1. Зависимость теплового эффекта реакции от температуры

можно получить, если формулу (3.29) с T₀ = 298,15 К подставить в формулу (3.28):

(3.31)

Дифференциальная форма температурной зависимости энтальпии реакции носит название уравнения Кирхгоффа

. (3.32)

Если в данном температурном интервале _rC_Р > 0, то при повышении температуры энтальпия возрастает, и наоборот.

Ранее определив другую важнейшую функцию – энтропию, мы уже привели формулу (3.24), которая определяет стандартное ее значение по данным о теплоемкости и энтальпиям _trH фазовых и полиморфных превращений.

Заменив букву H буквой S вместо формул (3.27) и (3.28) для энтальпии получаем пропорциональное координате реакции изменение энтропии системы, выраженное через энтропию реакции .

, , (3.28')

В отличие от энергетических функций, 3-й закон термодинамики однозначно определяет нулевой уровень отсчета энтропии для каждого «нормального» вещества при 0 К.

Наконец, стандартные энтальпия и энтропия составляют стандартную энергию Гиббса реакции – её важнейшую термодинамическую характеристику: _rG = _rH – T_rS. (3.33)

3.6. Энтропия идеального газа и идеальной газовой смеси.

Подставив дифференциал мольного объема идеального газа в основное термодинамическое соотношение TdS  = C_V dT + РdV и использовав связь (3.20) C_V = C_P – R получаем . Интегрирование от T₁ и P₁  до Т и Р даёт .

Энтропийная постоянная идеального газа S′ при конкретизированных T₁ = 1 К, P₁ = P = 101325 Па = 1 атм – это энтропия 1 моля газа при стандартном давлении P и температуре 1 К может быть вычислена методами статистической термодинамики по молекулярным постоянным. Т. о. абсолютная энтропия моля идеального газа

, (3.35)

где стоящие под знаком ln T = T/1К и - безразмерные величины.

В стеклянный цилиндр, разделенный перегородками, поместим по ni молей разных газов. P и T во всех отсеках одинаковы.

S_{(до смешения)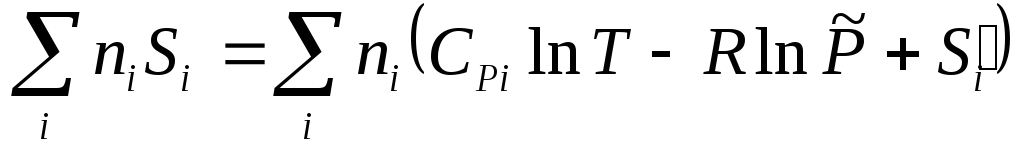} = (3.36)

После разрушения перегородок и необратимого (диффузионного) смешения каждый из газов займет весь объем. При этом температура останется неизменной, поскольку внутренняя энергия газа не зависит от объема. Одинаковое и равное давление P после разрушения перегородок становится общим давлением , которое по закону Дальтона складывается из парциальных, где- мольная доляi-го компонента в смеси.

Энтропия системы после смешения газов равна

S_{(после смешения)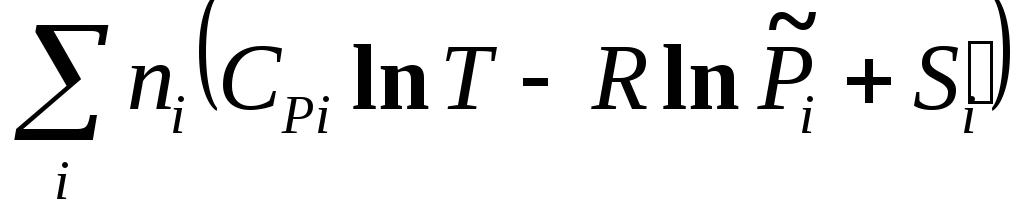} = . (3.37)

Изменение энтропии в результате смешения газов называют энтропией смешения S_см = S_{(после смешения)} – S_{(до смешения)} :

S_см = . (3.38)

Оказывается, что это выражение определяет энтропию смешения не только газовых, но и жидких и твердых идеальных растворов. При смешении компонентов энтропия системы необратимо возрастает.

3.7. Энергия Гиббса смеси. Химический потенциал компонента

в растворе

Определение основных понятий химической термодинамики и получение общих соотношений продолжим на примере идеально газовой системы.

Энтальпию i-го компонента при (необязательном) условии постоянства C_p легко получить из её определения (3.19):

H_i = C_РiT + H_0i , (3.39)

где H_0i = U_0i – внутренняя энергия моля идеального газа при 0 К.

Составим из иS (3.37) энергию Гиббса G = H – TS = 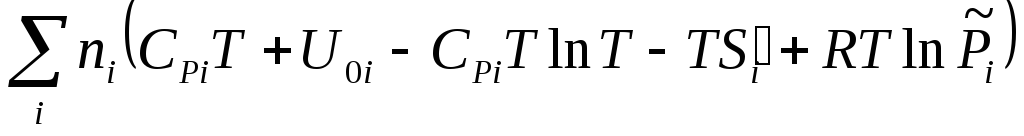. Объединив все слагаемые, которые зависят от природыi‑го вещества и температуры, но не зависят от состава смеси, получаем

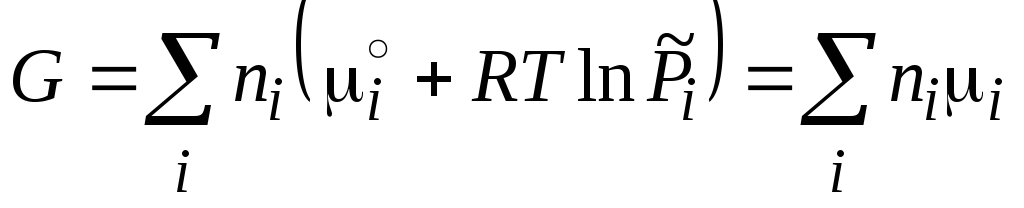, (3.40) . (3.41)

Величина μ_i называется химическим потенциалом i‑го компонента в газовой смеси. - стандартный химический потенциал компонента при парциальном давлении.

Используя определение парциального давления , из (3.41) получаем другую форму химического потенциала (),(3.41')

которую можно применять уже не только к газовым, но и к конденсированным смесям.

При протекании химических процессов происходит изменение состава реакционной смеси. Соответствующее изменение G:

, (3.42)

Можно показать, что , а из (3.42) следует фундаментальное определение химического потенциала(3.41'').

Являясь важнейшей характеристикой вещества в растворе, химический потенциал i‑го вещества - это, прежде всего, частная производная от энергии Гиббса по его мольному количеству в растворе.