Параметры цифровой подписи |
||
Параметрами схемы цифровой подписи являются: |
||
простое число р - модуль эллиптической кривой; |
|
|
эллиптическая кривая Е , задаваемая своим инвариантом J(E) или |
||
коэффициентами а,b |
; |
|
|
F |
|
целое число m - порядокpгруппы точек эллиптической кривой Е; |
||
простое число q - порядок циклической подгруппы группы точек |
||
эллиптической кривой Е, для которого выполнены следующие условия: |
||
|
|
(9) |
точка Р≠О эллиптической кривой Е , с координатами (хр , ур ) , |
||
удовлетворяющая равенству qP = О ; |
|
|
хэш-функция отображающая сообщения h (‘):V*→V l |
представленные в |
|
виде двоичных векторов произвольной конечной длины, в двоичные вектора |
||
длины l бит. Хэш-функция определена в ГОСТ Р 34.11-2012 |
|
|
Математические объекты. Параметры цифровой подписи
Каждый пользователь 
схемы цифровой подписи должен обладать личными
ключами:
ключом подписи - целым числом d , удовлетворяющим неравенству 0 < d < q ;
ключом проверки - точкой эллиптической кривой Q с координатами (хq , yq ),
удовлетворяющей равенству dP = Q .
Математические соглашения. Параметры цифровой подписи
На параметры схемы цифровой подписи
накладываются
требования:
должно бытьt выполнено условие p 1(mod p)
для всех целых t = 1, 2,254... В , где 256В=31, если
2 q 2
2508 q 2512 , и В=131, если
должно быть выполнено неравенство m ≠ p ;
инвариант кривой должен удовлетворять условию J(E) ≠0 или 0,1728.
Математические объекты. Двоичные векторы
Для определения процессов формирования и проверки цифровой подписи необходимо установить соответствие между целыми числами и двоичными
векторами длины l |
бит. |
Рассмотрим следующий двоичный вектор длиной l бит, в котором младшие биты расположены справа, а старшие – слева:
|
|
(10) |
|
где ,i i = 0, ...,l-1 равно либо 1, либо 0. |
|
Будем считать, что число |
|
Z |
|
|
|
|
|
|
|
соответствует двоичному вектору , еслиhвыполнено равенство: |
|||
l 1 |
|
(11) |
|
i 2 |
i |
||
|
|
|
|
i 0
Математические соглашения. Двоичные векторы
Для двух двоичных векторовh1 и h2 , соответствующих целым числам α и β ,
определим операцию конкатенации (объединения) следующим образом. Пусть:
|
|
h1 |
|
|
( l 1 ,..., 0 ) |
(12) |
|||||
|
|
|
|
|
|
|
|
|
( l 1 ,..., 0 ) |
||
|
|
h2 |
|||||||||
|
|
|
|||||||||
тогда их объединение имеет вид: |
|
(13) |
|||||||||
|
|
|
|
|
|
( l 1,..., 0 , l 1,..., 0 ) |
|||||
|
|
|
|
|
|
|
|||||
h1 |
h2 |
||||||||||
и представляет собой двоичный вектор длиной 2l бит, составленный из коэффициентов векторовh1 и h2.
С другой стороны, приведенные формулы определяют способ разбиения
двоичного вектора h1 длиной 2l бит на два двоичных вектора длиной l бит, конкатенацией которых он является.
Основные процессы
Механизм цифровой подписи определяется посредством реализации двух основных процессов :
- формирование подписи;
- проверка подписи.
Для реализации данных процессов необходимо, чтобы всем пользователям были известны параметры схемы цифровой подписи, удовлетворяющие требованиям.
Кроме того, каждый пользователь должен иметь ключ подписи d и ключ проверки подписи Q(x , y ) , которые также должны удовлетворять требованиям. q q
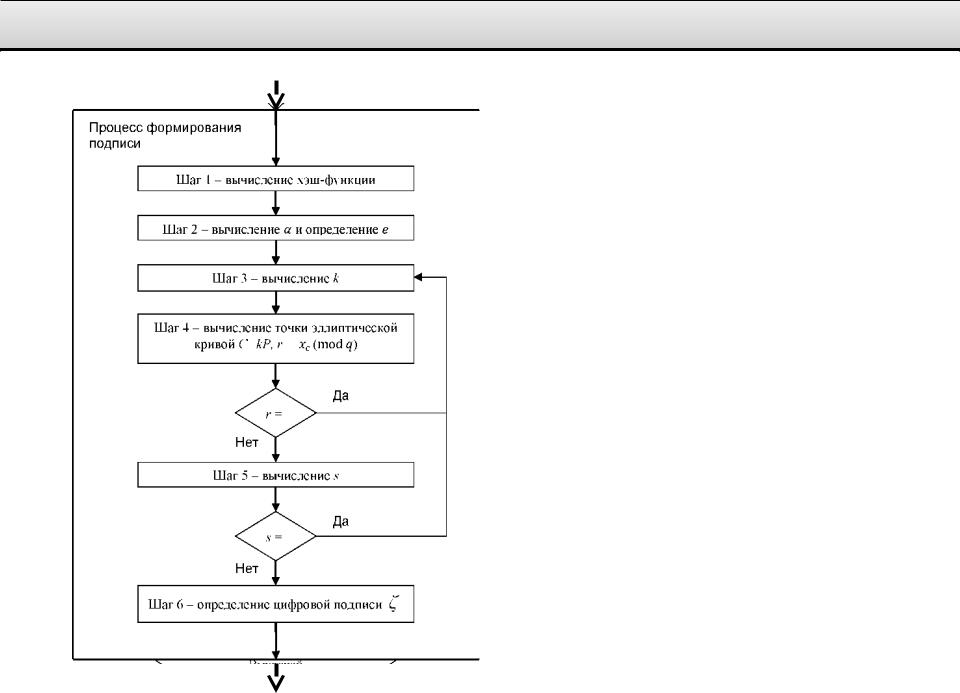
Основные процессы. Формирование цифровой подписи
Исходные данные
Выходной рез-т
Формирование цифровой подписи
Для получения цифровой подписи под сообщением необходимоM V *
выполнить следующие действия (шаги) по алгоритму I:
|
Шаг 1 |
- вычислить хэш-код сообщения |
|
|
|
|
|
|
|
|
|
|
(14 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
M : h h(M ) |
|
|
|
|||||||||||
|
Шаг 2 |
|
|
|
|
|
|
|
|
представлением которого |
|
||||||||||
|
- вычислить целое число а, двоичным |
|
|
|
|
|
|
|
) |
|
|
||||||||||
|
является вектор h , и определить |
|
e (mod q) |
|
(15 |
|
|
||||||||||||||
|
Если е = 0, то определить е = 1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Шаг 3 |
- сгенерировать случайное (псевдослучайное) целое число k , |
(16 |
|
|||||||||||||||||
|
удовлетворяющее неравенству |
|
0 < k < q . |
|
|
|
|||||||||||||||
|
Шаг 4 |
- вычислить точку эллиптической кривой C = kP и определить) |
|
||||||||||||||||||
|
|
|
|
|
|
r xc (mod q) |
|
|
(17 |
|
|||||||||||
|
Где xc - x -координата точки С . Если r = 0, то вернуться к шагу 3. |
) |
|
||||||||||||||||||
|
Шаг 5 |
- вычислить значение s (rd ke)(mod q) |
|
||||||||||||||||||
|
(18 |
|
|||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
Если s = 0, то вернуться к шагу 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
) |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
Шаг 6 |
- вычислить двоичные векторы |
r |
и |
|
|
, соответствующие r и s , |
|
||||||||||||
|
|
s |
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
векторов. |
|
(r || s) |
|
|
|
||||||||||||||||
и определить цифровую подпись |
|
|
|
|
|
|
|
|
|
|
|
|
как конкатенацию двух двоичных |
|
|||||||
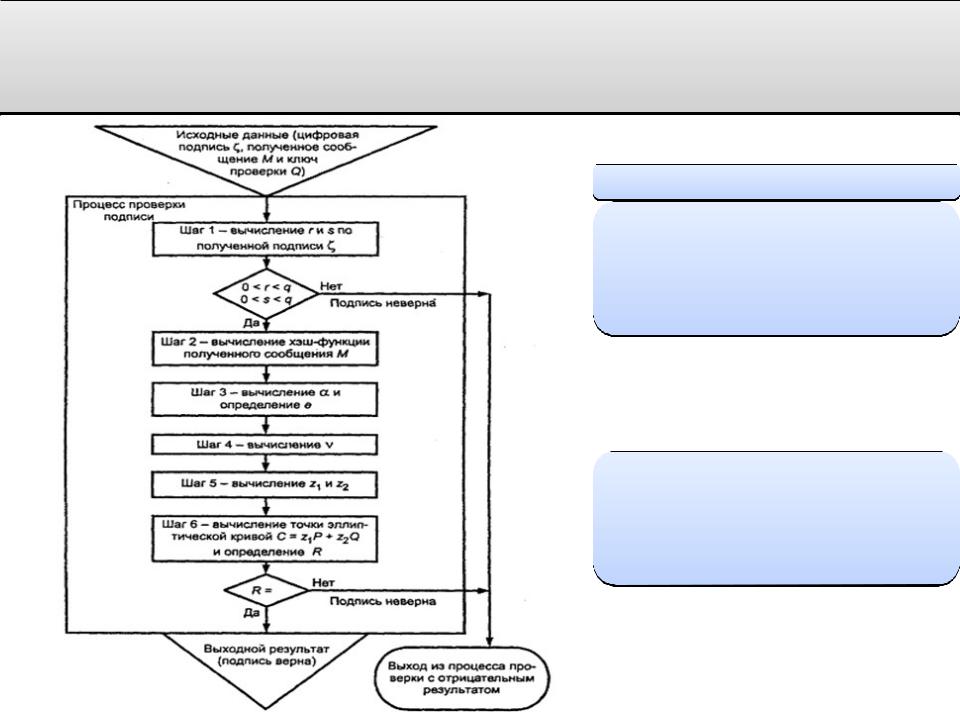
Основные процессы. Проверка цифровой подписи
Исходные данные:
• подписанное сообщение М
• цифровая подпись ζ
• ключ проверки Q
Выходной результат-
свидетельство о достоверности или ошибочности данной подписи.
Проверка цифровой подписи
Для проверки цифровой подписи ζ , под полученным сообщением М необходимо выполнить следующие действия (шаги) по алгоритму II:
Шаг 1 - по полученной подписи ζ вычислить целые числа r и s . Если выполнены неравенства 0 < r < q, 0 < s < q , то перейти к следующему шагу.
В противном случае подпись неверна.
|
Шаг 2 |
- вычислить хэш-код полученного |
|
сообщения М |
(19 |
|
|||
|
|
|
|
|
|
h |
h(M ) |
|
|
|
Шаг 3 - вычислить целое число |
|
, двоичным представлением которого |
|
|||||
|
|
|
|
α |
|
|
|
) |
|
|
Является |
вектор h , и определить |
|
|
|
(20 |
|
||
|
|
|
e (mod q) |
|
|||||
|
Если е = 0, то определить е = 1. |
|
|
|
|
) |
|
||
|
Шаг 4 |
- вычислить значение е 1 (mod q) |
|
||||||
|
(21 |
|
|||||||
|
|
|
|||||||
|
Шаг 5 |
- вычислить значения |
|
|
|
|
) |
(22 |
|
|
|
|
z1 sv(mod q), z2 rv(mod q) |
||||||
|
Шаг 6 |
- вычислить точку эллиптической кривой C z1P z2Q и определить |
|||||||
|
где xc - x -координата точки С . |
R xc (mod q) |
(23 |
) |
|||||
|
|
||||||||
|
Шаг 7 |
- если выполнено равенство R = r , то подпись принимается) . |
|
||||||
В противном случае, подпись неверна.