1. Свойства дискретного преобразования Фурье (ДПФ).

1. Фурье-спектр четной вещественной последовательности - вещественный.

Действительно.

Пусть , тогда

В частности, , то есть имеется бесконечная вещественная периодическая последовательность с периодом из N отсчетов.

2. Фурье-спектр нечетной вещественной последовательности – чисто мнимый.

Действительно.

Пусть , тогда

Отметим, что в этом случае , и

3. Для произвольной вещественной последовательности получается, что Re{ДПФ}- соответствует четная составляющая последовательности, а для Im{ДПФ}-нечетная составляющая.

4. Для произвольной вещественной последовательности с числом членов N-четным имеем: Re{ДПФ}-содержит (N/2+1) независимых отсчетов (0,1,2,…(N/2-1), N/2), Im{ДПФ}-содержит (N/2-1) независимых отсчетов (1,2,3,…(N/2-1)). Всего – N независимых отсчетов. Другими словами, комплексное (по определению) ДПФ избыточно ( 2N вместо N отсчетов).

5. Вставим в конец ДПФ (туда где уже частотные компоненты нулевые) ещё N нулевых отсчетов с тем же частотным шагом . Получим уже 2N частотных отсчетов при неизменном , что означает неизменность длительности сигнала ,увеличение ширины спектра ДПФ в 2 раза - и соответствующее уменьшение временного шага дискретизации (интерполяция подразделением в частотной плоскости в 2 раза).

6. Переставим m первых отсчетов в конец периода (на места N,N+1,…N+m-1). В результате получаем ту же бесконечную вещественную периодическую последовательность с периодом из N отсчетов, только сдвинутую на m отсчетов вперед. Тем самым у спектральных компонент появится фазовый множитель: .

7. Возьмем бесконечную вещественную периодическую последовательность , повторив последовательность 2 раза. Тем самым мы увеличили длительность в 2 раза () и уменьшили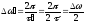 тоже в 2 раза. Но ДПФ новой последовательности ничем не отличается от старой, следовательно, посередине между спектральными отсчетами , по-прежнему следующими с интервалом , появятся нулевые отсчеты!

8. Следовательно (временная и частотная плоскости – «сладкая парочка»), справедливо и обратное: бесконечной вещественной периодической последовательности соответствует ДФП: . Другими словами, при вставке между отсчетов нулевых в бесконечную вещественную периодическую последовательность её спектр ДФП не изменился!

2. Показать аналитически, что вычисление непрерывного спектра Фурье от непрерывной периодической функции эквивалентно нахождению коэффициентов разложения этой функции в ряд Фурье.

Отсюда получаем, что F отличается от нуля только в точках , где n – целое число. А спектр в этих точках – дельта функция

( может, надо домножить на 2π)

(Achtung!!! Есть мнение, что это чушь!!!).

2. Как соотносятся между собой спектры Фурье одного видеоимпульса и последовательности (конечной или бесконечной) таких же видеоимпульсов?

Спектр бесконечной периодической последовательности видеоимпульсов – набор дельта-функций с частотами w₀,2*w₀,3*w₀.

Спектр одного видеоимпульса – непрерывный sinc. Если в последовательности N импульсов, которые повторяются через время T, то полученный спектр – спектр одного сигнала, умноженный на сумму фазовых сдвигов

2. Как соотносятся между собой спектры Фурье и результаты вычисления ДПФ?

Дискретное преобразование Фурье (временной подход)

Напомним:

- длительность сигнала.

ДПФ называются отсчеты спектра дискретной последовательности, взятые на протяжении одного периода спектра () с равным шагом (). Всего N штук.

().

Таким образом, , или, иначе говоря, огибающей отсчетов ДПФ является мультиплицированный спектр Фурье непрерывного сигнала, естественно, с учетом вполне реального эффекта наложения частот (aliasing) .

С учётом нормировки обратное преобразование ДПФ:

2. Алгоритм БПФ как метод циклической редукции.

Идея БПФ восходит первоначально еще к работам Гаусса, затем она была предложена в прикладной работе Даниэльсона и Ланцоша, а известность метод приобрел лишь через 23 года после очередного открытия Кули и Тьюки в 1965 году.

Принцип БПФ поясним на примере БАФ (позднее рассмотрим более подробно).

.

Представим: (циклическая редукция). Тогда

Тогда

Внутренняя сумма при фиксированном описывает независимые разложения Фурье для N₁ различных функций, каждая из которых составлена из значений исходной функции в N₂ узлах: i₁,i₁+N₁,…i₁+N-N₁ ,выбранных с шагом N₂ , начиная с узла i₁ . Для вычисления каждой внутренней суммы (по i₂ и n₂ ) требуется операций, а для всех - операций. Для вычисления внешней суммы требуется N₁ операций, а для всех N внешних сумм - операций. Всего получается - операций, вместо N² по «тупому» вычислению с использованием формул Бесселя.

Такая методика может быть применена к каждому из m возможных целых сомножителей N : . Тогда общее число операций составляет примерно: . Если принять , то и выигрыш составит примерно:. Легко установить, что при фиксированной длине реализации - N - выигрыш максимален при q=e. По техническим причинам обычно (было в СССР одно исключение) q=2 .В этом случае при N=1024=2¹⁰ выигрыш примерно 50.

2. Как нужно выбирать параметры ДПФ, чтобы по результатам его применения к сигналу можно было получить представление о спектре Фурье последнего?

Чтобы можно было бы судить о спектре Фурье периодической функции, интервал должен быть равен целому числу периодов, а частота дискретизации должна быть такой, чтобы полученные отсчеты спектра совпадали с частотами w,2*w,3*w … или хотя бы их содержали. При этом условии полученный спектр будет похож на истинный. Если это не выполняется, то, понятное дело, представление о спектре будет, мягко говоря, неверное.

2. Какова сущность метода интерполяции отсчётов фильтрацией в частотной области?

Спектр Фурье дискретной функции периодичен с периодом . Если функция дискретизирована с частотой выше частоты Найквиста, каждый период ее спектра представляет собой не искаженный наложениями спектр исходного непрерывного сигнала. Этот спектр может быть выделен, а исходный сигнал - восстановлен точно. Идеальная интерполяция промежуточных отсчетов при уменьшении в раз шага дискретизации включает следующие шаги:

1. повторить раз спектр исходной последовательности отсчетов;

2. обнулить среднюю часть спектра, содержащую период;

3. выполнить обратное преобразование Фурье

То есть, мы удлиняем спектр в N раз, добавляя нули. Потом вырезаем центральную часть, соответствующую высшим частотам, о которых у нас информации все равно нет. Далее делаем обратное преобразование и получаем интерполированный в N раз сигнал.

2. Чем определяется точность метода интерполяции отсчётов фильтрацией в частотной области?

Как и обычно – насколько влияют на спектр высшие частоты, которые искажают наш спектр. Еще – мы отсекаем часть с высшими частотами, и если они там не равны нулю, то здесь и будут расхождение с исходной функцией. Короче – точность должна определяться спектральной плотностью высших частот.

2. БПФ с прореживанием по частоте.

Прореживание по частоте

Пусть: - первая половина x_n ((N=2^p)-степень 2),

- вторая половина x_n .

При k=2m

,

При k=2m+1

2. БПФ с прореживанием по времени.

Прореживание по времени

Пусть:

.

Тогда:

Поскольку , получаем .

Подсчитаем количество необходимых для вычисления ДПФ операций.

Первый цикл: .

Следующий цикл: .

Далее:

.

Таким образом, на p-том шаге количество необходимых для вычисления ДПФ операций составит:

Выигрыш: .

2. Дискретное косинус-преобразование и его свойства.

Пусть имеется произвольная функция, определенная на интервале . Четно продолжим её на интервал . Получим четную функцию x(t), определенную на интервале .

Следовательно:

.

В дискретном виде. Дополним последовательность её зеркальным (четным) отображением и построим :

. В частности, и, соответственно, последовательность симметрична относительно (t=0).

Пусть ,

тогда .

- нечетная последовательность (так как от k вообще не зависит!), поэтому и . Следовательно, остается ровно N отсчетов!

Действительно: Таким образом, дискретное косинус-преобразование переводит N вещественных отсчетов по времени в N отсчетов по частоте (тем самым, лишено избыточности ДПФ) и дает минимум ненулевых отсчетов из-за высокой степени гладкости сконструированной последовательности .

В заключение, рассмотрим обратное дискретное косинус-преобразование.

Учтено, что -нечетная последовательность и ;

Осуществлен переход от к , а затем обратно простой заменой индексов (k=2N-k) .

2. Сравнение свойств ДКП и ДПФ.