6. Нормальная диагональная форма Смита.

Рассмотрим вопрос, к какому простейшему виду можно привести матрицу гомоморфизма за счёт изменения базиса решёток. Из предыдущего материала следует, что данный вопрос можно свести к следующему вопросу.

К какому простейшему виду можно привести матрицу с целочисленными элементами, используя элементарные преобразования со строками и столбцами? Ответ на этот вопрос содержится в п.2.6.1.

Близкий по содержанию вопрос: эквивалентны ли две заданные целочисленные матрицы. В п.2.6.2 даётся критерий, позволяющий получить ответ на этот вопрос.

Нормальной диагональной формой Смита называется матрица, ненулевые элементы которой расположены только на главной диагонали, причём каждый следующий элемент делится без остатка на предыдущий элемент.

1. Существование нормальной диагональной формы Смита.

Алгоритм 2 .1, применённый к произвольной матрице с целочисленными элементами, приведёт её к треугольному виду, используя элементарные преобразования только со строками. Дадим описание алгоритма, который элементарными преобразованиями со строками и столбцами приводит матрицу A из к нормальной диагональной форме Смита.

Алгоритм 2.2 Построение нормальной диагональной формы Смита.

1. Положим k=1.

2. Если k>n, или k>m, или все элементы матрицы расположенные в последних m-k строках и n-k столбцах равны нулю, то алгоритм работу закончил. Иначе перейдём на следующий шаг.

3. Перестановкой строк и столбцов с номерами не меньше k, и возможно умножением k-ой строки на -1, добьёмся, чтобы на пересечении k-ой строки и k-го столбца стояло положительное число, являющееся наименьшим по абсолютной величине среди ненулевых элементов матрицы, расположенных в её последних m-k строках и n-k столбцах (). Перейдём на следующий шаг.

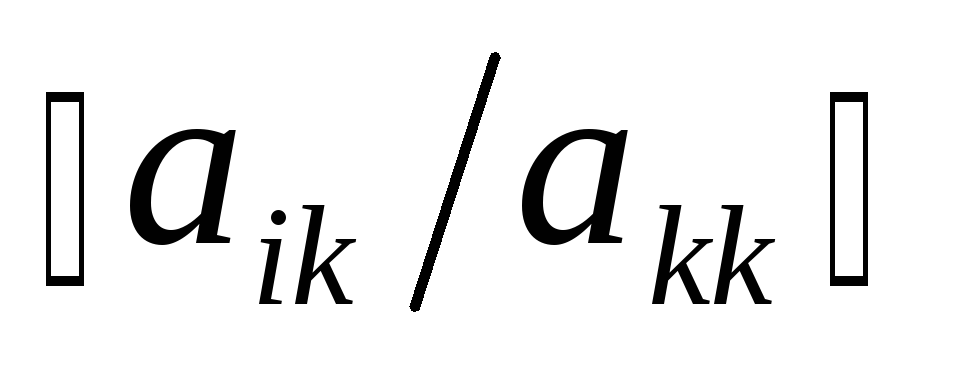4. Если все элементы k-го столбца, расположенные ниже главной диагонали, равны нулю, то перейдём на шаг 5. Иначе найдём такой номер строки i, что . Затем вычтем изi-ой строки k-ую строку умноженную на число и вернёмся на шаг 3.

5. Если все элементы k-ой строки, расположенные правее главной диагонали, равны нулю, то перейдём на шаг 6. Иначе найдём такой номер столбца j, что . Затем вычтем изj-ого столбца k-ый столбец умноженный на число и вернёмся на шаг 3.

6. Если делится набез остатка при любыхi,j>k, то увеличим k на 1 и вернёмся на шаг 2. В противном случае найдём такие номера i,j>k, что не делится набез остатка. Тогда прибавим кk-ому столбцу j-ый столбец и вернёмся на шаг 4.

Для обоснования алгоритма достаточно заметить, что элемент положителен и на каждом шаге может только уменьшаться. Следовательно, за конечное число шагов произойдёт увеличениеk, и, значит, алгоритм конечен. Тем самым установлена теорема.

Теорема 2.5. Для каждой матрицы существует эквивалентная ей нормальная диагональная форма Смита.

2. Единственность нормальной диагональной формы Смита.

Покажем, что для каждой матрицы существует только одна нормальная диагональная форма Смита, эквивалентная ей. Пусть ранг матрицы A размерами равенr. Обозначим через наибольший общий делитель миноровi-го порядка матрицы А (i=1,..,r)..

Лемма 2.2. Если матрицы A и B эквивалентны, то , гдеi=1,…,r.

Доказательство. Так как матрицы A и B эквивалентны, то найдутся унимодулярные матрицы P и Q, что A=PBQ. Для простоты рассмотрим случай, когда матрица Q - единичная. Унимодулярная матрица представляется в виде произведения матриц элементарных преобразований (Теорема 2 .4). Следовательно, не нарушая общности, можно считать, что матрица P является матрицей элементарных преобразований. Отметим, что перестановка строк, умножение строки на -1 не меняет (с точностью до знака) множество миноров i-го порядка, а значит и их наибольший общий делитель. Таким образом, единственное элементарное преобразование, представляющее интерес, состоит в прибавлении к s-ой строке j-ой строки, умноженной на целое число. В этом случае все миноры i-го порядка матрицы B либо равны соответствующим минорам матрицы A, либо являются их комбинацией с целочисленными коэффициентами. В обоих случаях минор i-го порядка матрицы B делится без остатка на , а значит,делится набез остатка. МатрицаA получается из матрицы B вычитанием s-ой строки из j-ой строки, умноженной на то же самое число. Рассуждая аналогично, выводим факт делимости без остатка на, что возможно только в случае равенства.

Разберём теперь случай, когда Q - произвольная унимодулярная матрица. Положим C=BQ. Как уже установлено ранее, справедливо равенство . При транспонировании миноры матрицC и B не изменятся, поэтому и. Из равенстваи доказанного ранее следует. Объединяя полученные равенства выводим утверждение леммы.

Пусть - нормальная диагональная форма Смита, эквивалентная матрицеA. Легко получить равенства , гдеi=1,…,k. Отсюда находим и, приi=2,…,k. В полученных формулах матрицу S можно заменить матрицей A (Лемма 2 .2). Таким образом, элементы матрицы S однозначно вычисляются по элементам матрицы A, а значит, доказана теорема.

Теорема 2.6. Для матрицы существует единственная нормальная диагональная форма Смита, эквивалентная ей. Не нулевые диагональные элементы нормальной диагональной формы Смита вычисляются по формулам, гдеi=1,…,r, и .

Сформулируем теперь критерий эквивалентности матриц.

Теорема 2.7. Матрицы A и B из эквивалентны тогда и только тогда, когда равны их рангиrgA=rgB=r и , приi=1,…,r.

Доказательство. Необходимость установлена выше (Лемма 2 .2). Покажем достаточность. Из условий теоремы следует, что матрицы A и B имеют одинаковую нормальную диагональную форму Смита, которую обозначим S. Алгоритм 2 .2, применённый к матрице A, построит унимодулярные матрицы P и Q, удовлетворяющие равенству PAQ=S. Аналогично, построим унимодулярные матрицы T и V, удовлетворяющие равенству TBV=S. Приравняв левые части полученных равенств PAQ=TBV, убедимся в эквивалентности матриц A и B.