3. Матрица гомоморфизма.

Определение 2.10 Однозначное отображение решёткив решётку, сохраняющее операцию (т.е.), называется гомоморфизмом решёток.

Приведённое определение гомоморфизма аналогично определению гомоморфизма абелевых групп.

Изоморфизм является частным случаем гомоморфизма, и может быть определён как взаимно однозначный гомоморфизм.

Гомоморфизм полностью определяется своими значениями на базисных векторах. Пусть базис решётки, а- базис решётки. Разложим образы базисных векторовпо базису:i=1,…,n. Матрица , составленная из координат образов базисных векторов, называетсяматрицей гомоморфизма. Из определения вытекает, что матрица гомоморфизма имеет размеры , а её элементы суть целые числа. Матрица гомоморфизма связывает координаты вектораx решётки в базисес координатами его образа в базисепо формуле.

Фиксация базисов в решётках иустанавливает взаимно однозначное соответствие между гомоморфизмами и матрицами из. Таким образом, изучение гомоморфизмов решёток сводится к изучению свойств матриц из.

4. Изменение матрицы гомоморфизма при изменении базиса решёток.

Матрица гомоморфизма зависит от выбора базиса в решётках и. Естественно, возникает вопрос о связи матриц гомоморфизма в разных базисах.

Пусть и- базисы решётки, аD - матрица перехода от базиса к базису. Аналогично, пустьи- базисы решётки, аF матрица перехода от базиса к базису. По определению матрицы гомоморфизма выполняется равенство. Запишем его в виде, откуда. По определению матрицы гомоморфизма имеем. В силу единственности матрицы гомоморфизма получаем равенство. Положит. МатрицаT является матрицей перехода от базиса к базису.

Формула показывает, как связаны матрицы одного и того же гомоморфизма в разных базисах. Следует подчеркнуть, что матрицыT и D являются унимодулярными.

Матрицы A и B, связанные отношением A=TBD, где T, D - унимодулярные матрицы, называются эквивалентными.

5. Элементарные преобразования.

Среди унимодулярных матриц особую роль играют матрицы элементарных преобразований. Своё название эти матрицы получили благодаря следующему факту. Умножение слева (или справа) на матрицу элементарных преобразований равносильно выполнению одного из следующих действий (элементарных преобразований).

1. Перестановка строк (столбцов) с номерами i и j.

2. Прибавление к i-ой строке(столбцу) j-ой строки (столбца) умноженной на целое число .

3. Умножение i-ой строки (столбца) на -1.

Отсюда видно, что матрица элементарных преобразований отличается от единичной матрицы

1. Перестановкой строк i и j.

2. Элементом, расположенным на пересечении i-ой строки (столбца) и j-го столбца (строки) и равного .

3. i-ой строкой, умноженной на -1

Легко проверить, что матрица элементарных преобразований является унимодулярной, и матрица, обратная к матрице элементарных преобразований, так же является матрицей элементарных преобразований.

Опишем алгоритм, приводящий с помощью элементарных преобразований произвольную унимодулярную матрицу A к единичной матрице.

Алгоритм 2.1. Разложение унимодулярной матрицы в произведение матриц элементарных преобразований.

1. Положим k=1.

2. Если k=n, то алгоритм работу закончил. Иначе перейдем на следующий шаг.

3. Если все элементы k-го столбца, расположенные ниже главной диагонали, равны нулю, то увеличим k на единицу и вернёмся на шаг 2. Иначе найдём номер строки i в котором расположен наименьший по абсолютной величине не нулевой элемент среди элементов расположенных ниже главной диагонали.

4. Переставим строки i и k. Если необходимо, то умножением k-ой строки на -1, добьёмся положительности элемента .

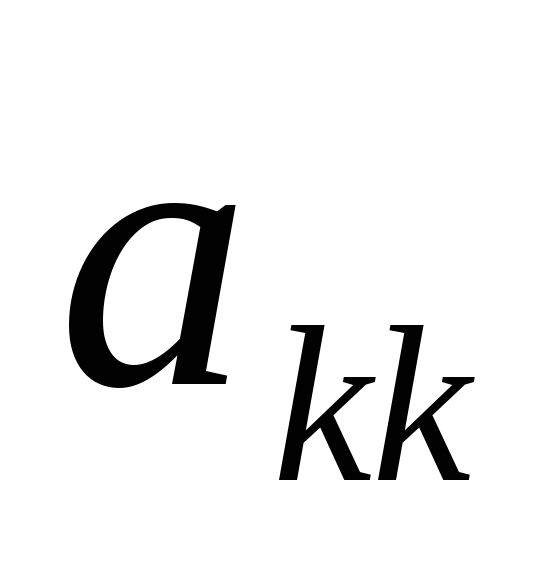5. Из каждой строки матрицы с номером i, где i неравно k, вычтем k-ую строку, умноженную на число 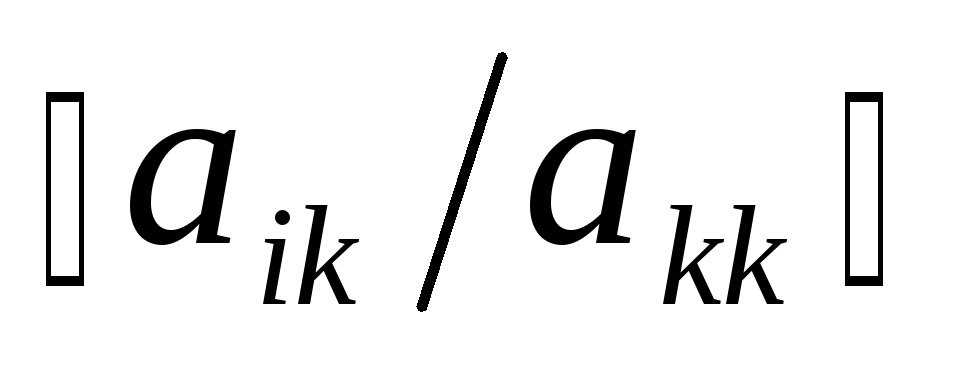. Вернёмся на шаг 3.

После выполнения шага 5, все элементы матрицы, расположенные в k-ом столбце, станут, по абсолютной величине, меньше элемента . Выполнение шагов 3-5 приводит к уменьшению элемента. Уменьшится элементможет лишь конечное число раз, поэтому, через конечное число итераций произойдёт увеличениеk на 1. После работы алгоритма, матрица будет иметь треугольный вид, причём по диагонали расположены положительные числа. Из унимодулярности матрицы следует, что все числа, расположенные по диагонали равны 1, а значит, матрица стала единичной. Обозначим через матрицу элементарных преобразований, полученную в процессе работы алгоритма, s-ую по порядку. Количество элементарных преобразований матрицы A, выполненных алгоритмом, пусть равно r. Равенство запишем в следующем виде. Поскольку обратная к матрице элементарных преобразований является также матрицей элементарных преобразований, то тем самым доказана теорема.

Теорема 2.4. Унимодулярная матрица разлагается в произведение матриц элементарных преобразований.

Из приведённой теоремы вытекает, что матрицы эквивалентны тогда и только тогда, когда от одной к другой можно перейти с помощью элементарных преобразований строк и столбцов.