
- •Введение в геометрию чисел. Алгоритмы и приложения.
- •Список обозначений.
- •Решетки
- •Дискретные множества.
- •Решётка и подрешётка.
- •Конечно порожденные решётки.
- •Базис решётки
- •Эквивалентное определение решётки.
- •Гомоморфизм решёток
- •Изоморфизм решёток
- •Базисы решётки, матрица перехода.
- •Матрица гомоморфизма.
- •Изменение матрицы гомоморфизма при изменении базиса решёток.
- •Элементарные преобразования.
- •Нормальная диагональная форма Смита.
- •Существование нормальной диагональной формы Смита.
- •Единственность нормальной диагональной формы Смита.
- •Эрмитова форма матрицы.
- •Существование эрмитовой формы.
- •Единственность эрмитовой формы.
- •Базисы решётки и подрешёток.
- •Выбор базиса решётки.
- •Дополнение до базиса решётки.
- •Линейные преобразования решёток.
- •Двойственная решётка
- •Эффективные алгоритмы, связанные с построением базиса решётки.
- •Алгоритм, его трудоёмкость. Понятие эффективного алгоритма.
- •Решение системы линейных уравнений в целых числах.
- •Полностью целочисленный вариант метода Гаусса.
- •Решение системы линейных уравнений в целых числах
- •Некоторые задачи на построение базиса решётки.
- •Построение нормальной диагональной формы Смита.
- •Построение эрмитовой формы.
- •Теоремы Блихфельда и Минковского.
- •Теорема Блихфельда
- •Теорема Минковского
- •Теоремы о близости
Построение нормальной диагональной формы Смита.
Описанный ранее алгоритм (см. п.2.6.1) построения нормальной диагональной формы Смита не является эффективным из-за возможного роста промежуточных величин. Ограничить рост промежуточных величин можно, если все алгебраические операции проводить по модулю d, где d - некоторый минор максимального порядка матрицы A. Приведём эффективный алгоритм построения нормальной диагональной формы Смита матрицы А, основанный на этой идее.
Алгоритм 4.7. Эффективный алгоритм построения нормальной диагональной формы Смита.
Целочисленным вариантом метода Гаусса (Алгоритм 4 .4) найдём ненулевой минор матрицы A максимального порядка. Положим его равным d.
Положим k=1.
Если k>n, или k>m, или все элементы матрицы расположенные в последних m-k строках и n-k столбцах равны нулю, то алгоритм работу закончил. Иначе перейдём на следующий шаг.
Перестановкой строк и столбцов с номерами не меньше k, и возможно умножением k-ой строки на -1, добьёмся, чтобы на пересечении k-ой строки и k-го столбца стояло положительное число, являющееся наименьшим по абсолютной величине среди ненулевых элементов матрицы, расположенных в её последних m-k строках и n-k столбцах (
 ).
Перейдём на следующий шаг.
).
Перейдём на следующий шаг.Если все элементы k-го столбца, расположенные ниже главной диагонали, равны нулю, то перейдём на шаг 6. Иначе найдём такой номер строки i, что
 .
Затем вычтем изi-ой
строки k-ую
строку умноженную на число
.
Затем вычтем изi-ой
строки k-ую
строку умноженную на число
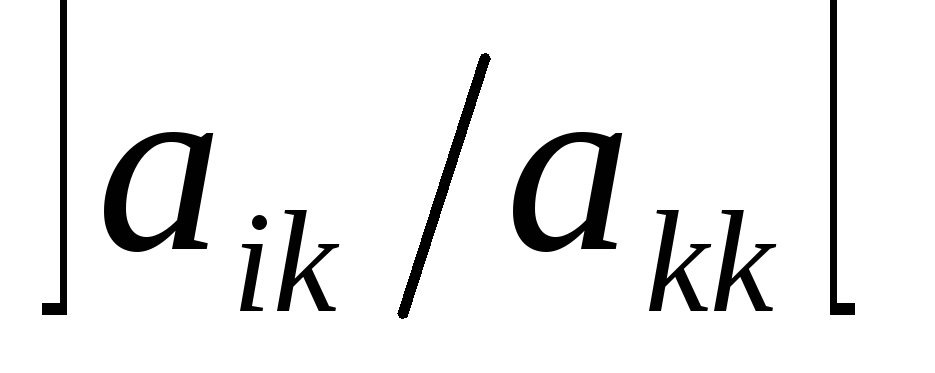 .
На месте каждого элемента матрицыA
поставим его остаток от деления на d.
Вернёмся на шаг 4.
.
На месте каждого элемента матрицыA
поставим его остаток от деления на d.
Вернёмся на шаг 4. Если все элементы k-ой строки, расположенные правее главной диагонали, равны нулю, то перейдём на шаг 7. Иначе найдём такой номер столбца j, что
 .
Затем вычтем изj-ого
столбца k-ый
столбец умноженный на число
.
Затем вычтем изj-ого
столбца k-ый
столбец умноженный на число
 .
На месте каждого элемента матрицыA
поставим его остаток от деления на d.
Вернёмся на шаг 4.
.
На месте каждого элемента матрицыA
поставим его остаток от деления на d.
Вернёмся на шаг 4.Если
 делится на
делится на без остатка при любыхi,j>k,
то увеличим k
на
1 и вернёмся на шаг 2. В противном случае
найдём такие номера i,j>k,
что
без остатка при любыхi,j>k,
то увеличим k
на
1 и вернёмся на шаг 2. В противном случае
найдём такие номера i,j>k,
что
 не делится на
не делится на без остатка. Тогда прибавим кk-ому
столбцу j-ый
столбец и вернёмся на шаг 5.
без остатка. Тогда прибавим кk-ому
столбцу j-ый
столбец и вернёмся на шаг 5.
Покажем корректность работы алгоритма. Обозначим через S нормальную диагональную форму Смита матрицы A. Не нулевые диагональные элементы матрицы S являются делителями d. Элементарными преобразованиями строк и столбцов (шаги 2-7) приведем матрицу А к некоторой нормальной диагональной форме B. При этом, найдутся унимодулярные матрицы P и T, что B=PAT+dF, где F - матрица с целочисленными элементами. Таким образом, матрицы S и B-dF - эквивалентны, что возможно только в случае S=B (см. Теорема 2 .6, Теорема 2 .7).
Оценим трудоёмкость
работы алгоритма. Наибольший по абсолютной
величине элемент матрицы A
обозначим через
![]() .
Трудоёмкость первого шага алгоритма
не превосходит
.
Трудоёмкость первого шага алгоритма
не превосходит![]() ,
а величинаd
не больше
,
а величинаd
не больше
![]() .
Выполнение пятого или шестого шагов
алгоритма гарантирует уменьшение
элемента
.
Выполнение пятого или шестого шагов
алгоритма гарантирует уменьшение
элемента![]() ,
по крайней мере, в 2 раза. При выполнении
других шагов алгоритма, элемент
,
по крайней мере, в 2 раза. При выполнении
других шагов алгоритма, элемент![]() не изменится. Поскольку все элементы
матрицыA
на любом шаге не превосходят d,
то число повторений шагов 5 и 6 не более
не изменится. Поскольку все элементы
матрицыA
на любом шаге не превосходят d,
то число повторений шагов 5 и 6 не более
![]() .
При выполнении шагов 2-7 потребуется не
болееO(mn)
арифметических операций. Поскольку
.
При выполнении шагов 2-7 потребуется не
болееO(mn)
арифметических операций. Поскольку
![]() ,
то общее число арифметических операций
алгоритма не превосходит
,
то общее число арифметических операций
алгоритма не превосходит![]() .
Все промежуточные результаты, возникающие
в ходе работы алгоритма, ограничены по
длине
.
Все промежуточные результаты, возникающие
в ходе работы алгоритма, ограничены по
длине![]() ,
значит, трудоёмкость алгоритма не
превосходит
,
значит, трудоёмкость алгоритма не
превосходит![]() .
.
Алгоритм 4 .7 строит
нормальную диагональную форму Смита
матрицы A,
но не находит унимодулярные матрицы,
приводящие к нормальной диагональной
форме Смита. Если A
- квадратная невырожденная матрица, то
легко модифицировать алгоритм так,
чтобы он находил и унимодулярные матрицы.
Припишем к матрице A
единичные матрицы справа и снизу (для
запоминания элементарных преобразований
со строками и столбцами, соответственно).
После работы алгоритма, будут найдены
унимодулярные матрицы P
и T,
удовлетворяющие равенству PAT=S+dF,
где F
- целочисленная матрица. Так как d
- величина определителя матрицы А,
то
![]() -
целочисленная
матрица. Далее, имеем
-
целочисленная
матрица. Далее, имеем
![]() .
Из равенства
.
Из равенства![]() следует равенство определителей
следует равенство определителей![]() ,
и унимодулярность матрицыP-H.
,
и унимодулярность матрицыP-H.
Если матрица A не является квадратной, или является вырожденной, то для построения унимодулярных матриц, приводящих матрицу A к нормальной диагональной форме Смита, можно воспользоваться следующим алгоритмом.
Алгоритм 4.8. Эффективный алгоритм приведения матрицы к нормальной диагональной форме Смита.
Применим Алгоритм 4 .5 для решения системы
 .
В результате вычислим:r-
ранг матрицы A,
d
- наибольший общий делитель миноров
r-го
порядка матрицы A,
P
-
унимодулярная матрица, что в матрице
PA
последние m-r
строк равны нолю.
.
В результате вычислим:r-
ранг матрицы A,
d
- наибольший общий делитель миноров
r-го
порядка матрицы A,
P
-
унимодулярная матрица, что в матрице
PA
последние m-r
строк равны нолю.Применим Алгоритм 4 .5 для решения системы Ax=0. В результате найдём такую унимодулярную матрицуT, что в матрице AT последние n-r столбцов равны нолю.
Произведение матриц PAT имеет блочный вид
 ,
гдеB
- квадратная
невырожденная матрица порядка k.
Применив Алгоритм 4 .7 к матрице B,
найдём её нормальную диагональную
форму Смита S
и унимодулярные матрицы H
и G,
удовлетворяющие равенству HBG=S.
Легко убедиться, что
,
гдеB
- квадратная
невырожденная матрица порядка k.
Применив Алгоритм 4 .7 к матрице B,
найдём её нормальную диагональную
форму Смита S
и унимодулярные матрицы H
и G,
удовлетворяющие равенству HBG=S.
Легко убедиться, что
 ,
и, значит, искомые унимодулярные матрицы
равны
,
и, значит, искомые унимодулярные матрицы
равны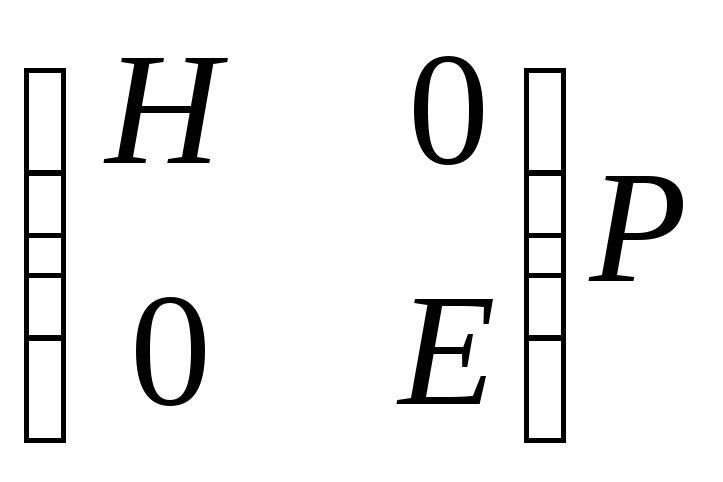 и
и .
.
Приведём оценку
трудоёмкости данного алгоритма.
Трудоёмкость первого шага не превосходит
![]() ,
а второго -
,
а второго -![]() .
При оценке третьего шага алгоритма
можно заметить, что элементы матрицыB
можно вычислять по модулю d.
Поэтому, трудоёмкость построения
нормальной диагональной формы матрицы
B
не превосходит
.
При оценке третьего шага алгоритма
можно заметить, что элементы матрицыB
можно вычислять по модулю d.
Поэтому, трудоёмкость построения
нормальной диагональной формы матрицы
B
не превосходит
![]() .
Верхняя оценка трудоёмкости построения
матрицH
и G
не превосходит
указанной величины. Таким образом,
трудоёмкость третьего шага алгоритма
(без учёта перемножения матриц)
не превосходит
.
Верхняя оценка трудоёмкости построения
матрицH
и G
не превосходит
указанной величины. Таким образом,
трудоёмкость третьего шага алгоритма
(без учёта перемножения матриц)
не превосходит
![]() .
Учитывая неравенство
.
Учитывая неравенство![]() ,
находим верхнюю оценку трудоёмкости
алгоритма
,
находим верхнюю оценку трудоёмкости
алгоритма![]() .
.
