3. Некоторые задачи на построение базиса решётки.

Пусть - система векторов из решётки. Рассмотрим следующие задачи:

1. Найти базис подрешётки , заданной как пересечение линейной оболочки векторовс решёткой.

2. Определить, является ли система векторов примитивной.

3. Дополнить примитивную систему векторов до базиса решётки.

4. Найти базис подрешётки , заданной как пересечение линейной оболочки векторовс решёткойи дополнить его до базиса решётки.

Обозначим через A матрицу, строки которой состоят из координат векторов . Найдемr - ранг матрицы A, d - наибольший общий делитель миноров максимального порядка, целочисленную невырожденную матрицу P и унимодулярную матрицу T, удовлетворяющие равенству (в левом верхнем углу матрицы, расположенной в правой части равенства, находится единичная матрицаr-го порядка). Для нахождения указанных величин и матриц воспользуемся алгоритмом построения общего целочисленного решения системы линейных уравнений (Алгоритм 4 .5).

Из равенства вытекает, что первыеr строк матрицы содержатся в подрешётке. МатрицаT - унимодулярная, значит, первые r строк матрицы образуют базис подрешётки. Таким образом, для решения первой задачи надо найти первыеr строк матрицы .

Для ответа на задачу 2 достаточно заметить, что система векторов является примитивной тогда и только тогда, когдаr=m и d=1 (Теорема 3 .13).

Поскольку система векторов - примитивная, то, и матрицаP - унимодулярная. Обозначим через F матрицу, образованную последними n-m строками матрицы . Справедливо равенство. МатрицыT и - унимодулярные, значит, матрица- то же унимодулярная. Таким образом, строки матрицыF дополняют примитивную систему векторов до базиса решётки. Тем самым установлено, для решения третьей задачи нужно найти последниеn-m строк матрицы .

Ранее установлено, что первые r строк матрицы образуют базис подрешётки. Последнимиn-r строками матрицы этот базис можно дополнить до базиса решётки.

При решении поставленных задач требуется строить не саму матрицу T, а обратную к ней. Матрица T получается в результате накопления элементарных преобразований со столбцами матрицы A. Пусть , где- матрица элементарного преобразования, тогда, где * обозначает операцию обращения и транспонирования матрицы (). При преобразовании матрицыA использовались элементарные преобразования двух типов.

1. Перестановка столбцов с номерами i и j.

2. Прибавление к i-му столбцу j-го столбца, умноженного на число t.

Умножение справа на матрицу , гдеT - матрица соответствующего элементарного преобразования, сводится к следующим элементарным преобразованиям.

1. Перестановка столбцов с номерами i и j.

2. Прибавление к j-му столбцу i-го столбца, умноженного на число -t.

Модифицируем алгоритм построения общего целочисленного решения системы линейных уравнений (Алгоритм 4 .5) для решения задач 1-4.

Алгоритм 4.6 Дополнение системы векторов до базиса решётки.

1. Применим Алгоритм 4 .4 к матрице A. При этом будут вычислены ранг матрицы r, и определитель некоторого минора максимального размера d. Положим T=E. Перестановками столбцов матрицы (если это необходимо) добьёмся, чтобы вr первых строках и столбцах матрицы A располагалась диагональная матрица, все диагональные элементы которой равны d.

2. К i-му столбцу матрицы T, где i=1,…,r прибавим линейную комбинацию её последних n-r столбцов . Пересчитаем элементы матрицыA по формулам , гдеi=1,…r, j=r+1,…,n.

3. Если , гдеi=1,…,r, j=r+1,…,n, то конец, алгоритм работу закончил. В противном случае найдём i,j, что 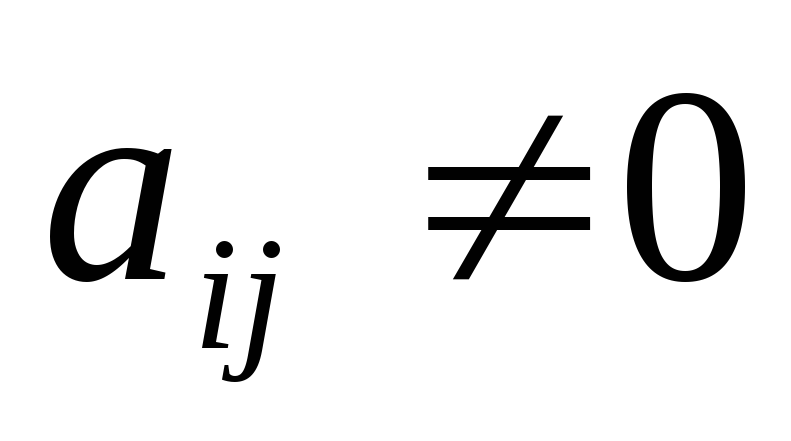и перейдём на шаг 4.

4. Поменяем местами i-ый и j-ый столбцы у матриц A и T. Из строки s матрицы A, где s=1,…,i-1,i+1,…,r, умноженной на , вычтемi-ую строку, умноженную на , и поделим каждый элемент полученной строкиs на d. После выполнения указанных операций со всеми строками с номерами s=1,…,i-1,i+1,…,k положим и вернёмся на шаг 2.

Обсудим работу предложенного алгоритма. На втором шаге алгоритма со столбцами матрицы A производятся следующие элементарные операции. Из j-го столбца матрицы вычитается i-ый столбец, умноженный на , гдеj=r+1,…,n, i=1,..,r. Поскольку все элементы i-го столбца равны нолю, кроме элемента расположенного в i-ой строке, равного d, то элементы матрицы A пересчитываются по формулам шага 2. Выполнение указанных преобразований равносильно умножению матрицы A справа на некоторую матрицу F. Умножение справа матрицы T на матрицу равносильно выполнению следующих элементарных преобразований со столбцами матрицыT. К i-му столбцу матрицы T прибавляется j-ый столбец, умноженный на , гдеj=r+1,…,n, i=1,..,r. Таким образом, в результате работы алгоритма будут построены r - ранг матрицы A, d - наибольший общий делитель миноров порядка r матрицы A, и унимодулярная матрица T, удовлетворяющая равенству .

Ответом первой задачи являются первые r - столбцов матрицы T. Чтобы исходная система векторов была примитивной необходимо и достаточно выполнения равенств m=r и |d|=1. Дополнением примитивной системы векторов до базиса решётки служат последние n-m столбцов матрицы T. При решении четвёртой задачи получим, что первые r столбцов матрицы T являются базисом подрешётки, заданной как пересечение линейной оболочки строчек матрицы A с решёткой , а остальные n-r столбцов матрицы T дополняют базис этой подрешётки до базиса решётки.

Трудоёмкость построенного алгоритма оценивается по той же схеме, что и трудоёмкость алгоритма построения целочисленного решения системы линейных уравнений (Алгоритм 4 .5). Здесь приведём только окончательную оценку его трудоёмкости .