2. Решение системы линейных уравнений в целых числах

Для нахождения общего целочисленного решения системы линейных уравнений воспользуемся следующим приёмом. Известно (см. Теорема 2 .7), что для любой матрицы A найдётся эквивалентная ей нормальная диагональная форма Смита S, то есть, найдутся унимодулярные матрицы P и F, что PAF=S. Если известны матрицы P и TF, то построение общего решения в целых числах системы линейных уравнений Ах=b не составляет труда. Для этого делаем замену переменных x=Fy и от системы AFy=b перейдем к равносильной ей PAFy=Pb=с. Последняя система выглядит следующим образом, …,,- любые целые числа. Соответственно, общее решение имеет вид. Умножая наT обе части равенства, получим - общее решение. Любое частное решение исходной системы получается подстановкой вместолюбых целых чисел. Заметим, что вместо нормальной диагональной формы Смита в данных построениях можно использовать любую диагональную матрицуD. Главное, что бы нашлись невырожденная (но целочисленная) матрица P и унимодулярная матрица F, удовлетворяющие равенству D=PAF. Для построения общего решения в целых числах системы уравнений матрица P на самом деле не нужна, а нужно произведение Pb. Используя эти замечания, модифицируем полностью целочисленный алгоритм Гаусса для нахождения общего целочисленного решения системы линейных уравнений. Для запоминания элементарных преобразований со столбцами, которые понадобятся для приведения матрицы к диагональному виду, припишем снизу к матрице A единичную матрицу. Таблицу вида обозначим черезT.

Алгоритм 4.5 Решение системы линейных уравнений в целых числах.

1. Применим Алгоритм 4 .4 к первым m строкам таблицы T. При этом будут вычислены ранг матрицы k, и определитель минора максимального размера d. Перестановками столбцов матрицы T (если это необходимо) добьёмся, чтобы в её первых k строках и столбцах располагалась диагональная матрица, все диагональные элементы которой равны d.

2. Из j-го столбца матрицы T, где j=k+1,…,n+1, вычтем линейную комбинацию первых k столбцов .

3. Если , гдеi=1,…,m, j=k+1,…,n, то конец, алгоритм работу закончил. В противном случае найдём i,j, что и перейдём на шаг 4.

4. Поменяем местами i-ый и j-ый столбцы матрицы T. Из строки s матрицы T, где s=1,…,i-1,i+1,…,k, умноженной на 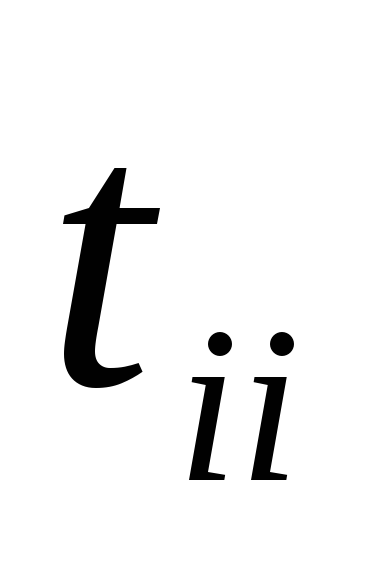, вычтемi-ую строку, умноженную на 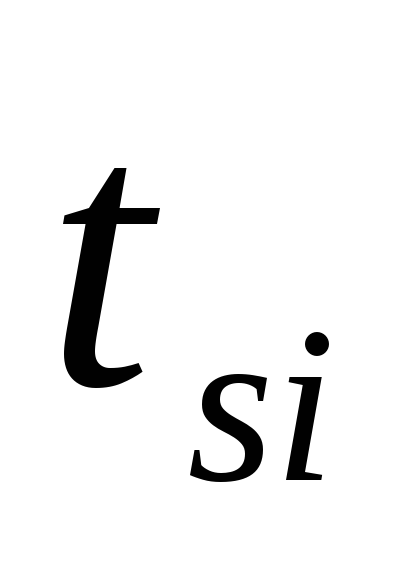, и поделим каждый элемент полученной строкиs на d. После выполнения указанных операций со всеми строками с номерами s=1,…,i-1,i+1,…,k положим и вернёмся на шаг 2.

Обсудим работу приведённого алгоритма. Во-первых, заметим, что при выполнении операции деления на шаге 4, остаток от деления равен 0. Действительно, выполнение операций со строками на шаге 4 проводится по тем же самым формулам, что и на шаге 5 полностью целочисленного алгоритма Гаусса (Алгоритм 4 .4). Следовательно, возможность деления без остатка вытекает из тех же самых соображений. Во вторых, выполнение шага 2 приводит к тому, что все элементы матрицы T, расположенные в последних n+1-k столбцах и первых k строках, по абсолютной величине не превосходят d/2. Значит, следующее попадание на второй шаг алгоритма возможно только при уменьшении d по крайней мере в два раза. Отсюда сразу вытекает конечность алгоритма. В третьих, после работы алгоритма, матрица T будет иметь следующий вид . Если хотя бы при одном номереi=1,…,m выполняется неравенство , то исходная система линейных уравнений несовместна в целых числах. В противном случае, общее решение имеет вид, где- целые числа.

Оценим трудоёмкость работы алгоритма в предположении целочисленности входной информации, причем наибольший по абсолютной величине из элементов матрицы (A,b) положим равным , иr=rg(A,b) Трудоёмкость шага 1 не превосходит (см. п.4.2.1). Последовательность шагов 2-4 назовём его итерацией. Присвоим каждой итерации алгоритма номер (начиная с 1). Номер последней итерации обозначим черезs. Величину d, используемую на j-ой итерации алгоритма, будем помечать вверху индексом, совпадающим с номером итерации. Для оценки длины промежуточных величин определим и- наибольшие по абсолютной величине из элементов матрицыT на j-ом шаге i-ой итерации алгоритма, расположенных в первых m и последних n строках, соответственно. Величина исовпадают с соответствующими минорами матрицы (A,b) и по неравенству Адамара, не превосходят ,. После выполнения второго шага алгоритма выполняются неравенстваи(см. формулы пересчёта). Далее,и, так как элементы матрицыT на третьем шаге не меняются. После выполнения четвёртого шага алгоритма выполняются соотношения ,, и . Последнее неравенство позволяет получить верхнюю оценку числа итераций алгоритма . Сгруппируем полученные неравенства отдельно дляu: ,,, и отдельно дляw: ,,. Последовательно применяя последнее неравенство, выводим.

Теперь можно оценить трудоёмкость i-ой итерации алгоритма (i>1). На втором шаге алгоритма потребуется не более O(rn) арифметических операций (включая деление с остатком) с элементами, по абсолютной величине не превосходящими иO(rn(n-r)) арифметических операций с элементами, по абсолютной величине не превосходящими . Таким образом, трудоёмкость второго шага i-ой итерации не превосходит . Трудоёмкость третьего шага не превосходитO(m(n-m)) (если трудоёмкость операции сравнения числа с 0 не превосходит O(1)). На четвёртом шаге потребуется не более O(rn) арифметических операций с элементами, ограниченными по абсолютной величине . Трудоёмкость четвёртого шага, таким образом, не превосходит. Общая трудоёмкостьi-ой итерации алгоритма не превосходит . Подставим в полученную оценку вместо величиниих верхние оценкии, соответственно. В результате получим следующую оценкутрудоёмкостиi-ой итерации алгоритма. Огрубим полученную оценку до . Перемножив полученную оценку на оценку числа итераций алгоритма, найдём верхнюю оценку трудоёмкости алгоритма.