Критерий Фишера (f-тест).

Оценка значимости уравнения регрессии в целом дается с помощью F-критерия Фишера. При этом выдвигается нулевая гипотеза, что коэффициент и, следовательно, факторх не оказывает существенного влияния на результат у.

F-тест определяет статистическую значимость коэффициента детерминации R².

Непосредственному расчету F-критерия предшествует анализ дисперсии. Центральное место в нем занимает разложение общей суммы квадратов отклонений переменной у от среднего значения на две части: «объясненную» и «необъясненную» регрессией:

=. (1)

общая объясненная остаточная сумма

сумма квадратов регрессией или

факторная сумма

квадратов

Если фактор х не оказывает влияние на результат, то есть и,то линия регрессии параллельна оси Ох и .Тогда вся дисперсия результативного признака обусловлена воздействием прочих факторов и общая сумма отклонений совпадает с остаточной.

Если же прочие факторы не влияют на результат, то у связан с х функционально и остаточная сумма квадратов равна нулю.

Поскольку не все точки поля корреляции лежат на линии регрессии, то всегда имеет место их разброс как обусловленный фактором х, то есть регрессией у по х, так и вызванный действием прочих причин (необъясненная вариация). Пригодность линии регрессии для прогноза зависит от того, какая часть общей вариации признака у приходится на объясненную вариацию. Очевидно, что если сумма квадратов отклонений, обусловленная регрессией, будет больше остаточной суммы квадратов, то уравнение регрессии статистически значимо и фактор х оказывает существенное влияние на результат у. Это равносильно тому, что коэффициент детерминации или будет приближаться к единице.

Любая сумма квадратов отклонений связана с числом степеней свободы независимого варьирования признака (фактора) х. Это число степеней свободы связано с числом единиц совокупности k (объем выборки) и с числом определяемых по этой выборке параметров или констант.

В парной регрессии определяем 2 константы: .

Применительно к каждой сумме (1) число степеней свободы должно показывать, сколько независимых отклонений из k возможных

(); ()…()

требуется для образования общей суммы квадратов. Так для образования общей суммы квадратов требуется (k-1) независимых отклонений, ибо свободно варьируют лишь (k-1) число отклонений (в силу того, что −это значит, что на эти отклонения наложена одна связь). Таким образом, мы можем заключить, что общая сумма квадратов имеет (k-1) степень свободы.

При расчете объясненной или факторной суммы квадратов используются теоретические (расчетные) значения результативного признака , найденные по линии регрессии: . В линейной регрессии ,, поэтому

.

Значит, факторная сумма квадратов при линейной регрессии зависит только от одной константы , и факторная сумма квадратов имеет одну степень свободы.

Существует равенство между числом степеней свободы общей, факторной и остаточной суммами квадратов. Таким образом, число степеней свободы для общей суммы квадратов равно (k-1), факторной суммы квадратов равно 1, для остаточной суммы квадратов равно (k-2).

Сумма квадратов	общая	факторная	остаточная
Степень свободы	(k-1)	1	(k-2)

Разделив каждую сумму квадратов на соответствующее ей число степеней свободы, получим средний квадрат отклонений, или, то же самое, дисперсию на одну степень свободы.

; ;.

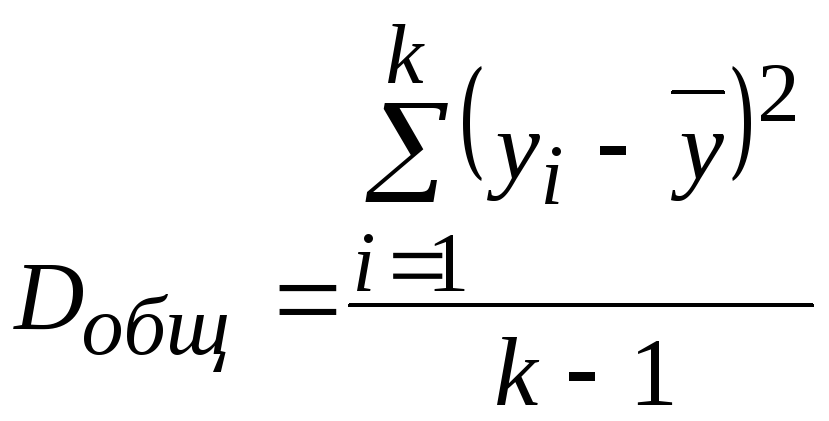Определение дисперсии на одну степень свободы приводит дисперсии к сравнимому виду. Сопоставляя и , получим величину F–отношения (F-критерий):

или .

Имеем .

F-критерий используется для проверки статистической значимости уравнения регрессии в целом. Выдвигается нулевая гипотеза Н₀, что у нас факторная сумма квадратов сравнима с остаточной, тогда уравнение регрессии статистически незначимо. Если нулевая гипотеза справедлива, то факторная и остаточная дисперсии не отличаются друг от друга .Для опровержения гипотезы Н₀ необходимо, чтобы факторная дисперсия превышала остаточную в несколько раз.

Английским статистиком Снедекором разработаны таблицы критических значений F –отношений при разных уровнях существенности нулевой гипотезы и различном числе степеней свободы. Табличное значение F-критерия – это максимальная величина отношения дисперсий, которая может иметь место при случайном их расхождении для данного уровня вероятности нулевой гипотезы. Вычисленное значение F –отношения признается достоверным (отличным от1), если оно больше табличного. В этом случае делается вывод о существенности связи признаков: ,то гипотезаотклоняется. Если же фактическая величина окажется меньше табличной, то вероятность нулевой гипотезы выше заданного уровня (например,или). В этом случае гипотезане отклоняется, и уравнение регрессии считается статистически незначимым. Признается ненадежность уравнения регрессии.

, в случае линейной регрессии ,.

Схема критерия:

Лекция 8